MATLAB实现一元三次方程求解/盛金公式

MATLAB实现一元三次方程求解/盛金公式

一元三次方程求解中，1945年卡尔丹诺把冯塔纳的三次方程求根公式发表出来，但该公式形式比较复杂，直观性也较差。1989年范盛金对一元三次方程求解进行了深入的研究和探索，提出了更加简洁实用的求解公式-盛金公式。这里对盛金公式进行简要的介绍，并给出MATLAB实现的具体代码和部分算例。参考资料：百度百科-卡尔丹公式；百度百科-盛金公式

一元三次方程求解–盛金公式

一元三次方程 $ax^3 +bx^2+cx+d=0$ 重根判别式令 $A=b^2-3ac$， $B=bc-9ad$， $C=c^2-3bd$总判别式 $\Delta=B^2-4AC$

下面给出盛金判别法的结论

条件1 当 $A=B=0$时： $x1=x2=x3= \frac{-b}{3a}= \frac{-c}{b}= \frac{-3d}{c}$
条件2 当 $\Delta=B^2-4AC>0$时： $x1= \frac{-b-(\sqrt[3]{Y1}+\sqrt[3]{Y2})}{3a}$ $x2=\frac{-b+0.5(\sqrt[3]{Y1}+\sqrt[3]{Y2})+ 0.5{\sqrt{3}} (\sqrt[3]{Y1}-\sqrt[3]{Y2})i}{3a}$ $x3=\frac{-b+0.5(\sqrt[3]{Y1}+\sqrt[3]{Y2})- 0.5{\sqrt{3}} (\sqrt[3]{Y1}-\sqrt[3]{Y2})i}{3a}$其中， $Y1=Ab+1.5a({-B+\sqrt{B^2-4AC}})$， $Y2=Ab+1.5a({-B-\sqrt{B^2-4AC}})$。
条件3 当 $\Delta=B^2-4AC=0$时： $x1= \frac{B}{A}- \frac{b}{a}$ $x2= x3= -\frac{B}{2A}$
条件4 当 $\Delta=B^2-4AC<0$时： $x1= \frac{-b-2\sqrt{A}cos{\frac{\theta}{3}}}{3a}$ $x2= \frac{-b+\sqrt{A}(cos{\frac{\theta}{3}}+\sqrt{3}sin{\frac{\theta}{3}}) }{3a}$ $x3= \frac{-b+\sqrt{A}(cos{\frac{\theta}{3}}-\sqrt{3}sin{\frac{\theta}{3}}) }{3a}$ 其中， $\theta=\arccos{T}$， $T=\frac{2Ab-3aB}{2A\sqrt{A}}$。
此外，推导得到的盛金定理表明任意实系数的一元三次方程都可以运用盛金公式解算
通过上述4个条件即可求得一元三次方程的所有根（实根和虚根）。

MATLAB代码-盛金公式

function x = Solve3Polynomial(a, b, c, d)
% 范盛金. 一元三次方程的新求根公式与新判别法[J]. 海南师范学院学报,1989,2(2):91-98.
A = b*b - 3*a*c;   if abs(A) < 1e-14;    A = 0;  end
B = b*c - 9*a*d;   if abs(B) < 1e-14;    B = 0;  end
C = c*c - 3*b*d;   if abs(C) < 1e-14;    C = 0;  end  
DET = B*B - 4*A*C; if abs(DET) < 1e-14;  DET = 0;  end  
if (A == 0) && (B == 0)
    x1 = -c/b;      x2 = x1 ;    x3 = x1;
end
if DET > 0
    Y1 = A*b + 1.5*a*(-B + sqrt(DET));
    Y2 = A*b + 1.5*a*(-B - sqrt(DET));
    y1 = nthroot(Y1,3);  y2 = nthroot(Y2,3);
    x1 = (-b-y1-y2)/(3*a);
    vec1 = (-b + 0.5*(y1 + y2))/(3*a);  
    vec2 = 0.5*sqrt(3)*(y1 - y2)/(3*a);
    x2 = complex(vec1, vec2);
    x3 = complex(vec1, -vec2);
    clear Y1 Y2 y1 y2 vec1 vec2;
end
if DET == 0 && (A ~= 0) && (B ~= 0)
    K = (b*c-9*a*d)/(b*b - 3*a*c); K = round(K,14);
    x1 = -b/a + K;   x2 = -0.5*K;   x3 = x2;
end
if DET < 0
    sqA = sqrt(A);
    T = (A*b - 1.5*a*B)/(A*sqA);
    theta = acos(T);
    csth  = cos(theta/3);
    sn3th = sqrt(3)*sin(theta/3);
    x1 = (-b - 2*sqA*csth)/(3*a);
    x2 = (-b + sqA*(csth + sn3th))/(3*a);
    x3 = (-b + sqA*(csth - sn3th))/(3*a);
    clear sqA T theta csth sn3th;
end
x = [x1;  x2;  x3];
end

值得说明的是：当得到的3个解中至少存在一个复数根时，matlab会将实数结果显示为 $a+0.0000000i$的形式。

算例验证

算例1： $x^3+5.4x^2+9.72x+5.832=0$

参考值： $x1=x2=x3=1.8$

算例2： $2x^3+11x^2+182x+255=0$

参考值： $x1=-1.5； x2=-2+9i；x3=-2-9i$

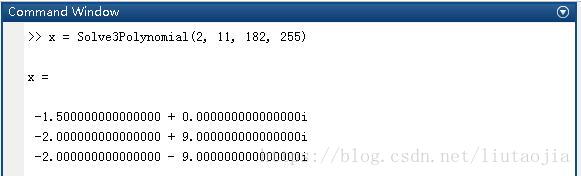
算例3： $x^3+5.5x^2+9.92x+5.888=0$

参考值： $x1=-2.3； x2=x3=-1.6$

算例4： $100x^3-420x^2+467x-105=0$

参考值： $x1=0.3； x2=2.5； x3=1.4$

上述4个算例可以看出，MATLAB实现过程中基本无误。