其实这个写起来是自己总结用的，当然如果能够帮助到你，那也是非常棒的一件事情
大部分的《算法竞赛进阶指南》上面都有，但这是我自己做的一些整理和总结。

DP其实在现在已经算是考烂掉的题目了，类型很多，题目很杂，但思想大概就是从已有结果当中选出当前阶段的结果了，本身是对于暴力枚举的最优性优化，利用记忆化减少了前置阶段的枚举。

DP优化其实是在枚举前置状态上的一个更优解的选择从而减少枚举的转移对象。复杂度大概都是从 $O(n^2)$ 优化到 $O(n)-O(nlogn)$ 不等。

主要利用到的工具是双端队列（单调队列），利用单调性维护所选择的决策转移方案。STL库当中也有，但这个其实手动维护一下就好了（STL真的很慢）。

数据结构优化

这一个优化主要是面对决策选择集合只会增大，不会减少的决策集合当中进行选择，就可以利用二叉堆，线段树，树状数组等等较高级的数据结构进行最优决策的优化。

【例题1】Cleaning Shifts（POJ2376）

Farmer John is assigning some of his N (1 <= N <= 25,000) cows to do some cleaning chores around the barn. He always wants to have one cow working on cleaning things up and has divided the day into T shifts (1 <= T <= 1,000,000), the first being shift 1 and the last being shift T.

Each cow is only available at some interval of times during the day for work on cleaning. Any cow that is selected for cleaning duty will work for the entirety of her interval.

Your job is to help Farmer John assign some cows to shifts so that (i) every shift has at least one cow assigned to it, and (ii) as few cows as possible are involved in cleaning. If it is not possible to assign a cow to each shift, print -1.

这个方程其实比较好写 $f[b_i]=min\left\{ f[x] \right\}+1 (a_i-1\leq x <b_i)$

但是显然这个的在枚举先前决策的时候数据太大，接近于 $O(n^2)$ ，所以需要利用数据结构维护转移方程当中的单调性。利用堆写一个struct，找出在条件范围内的最优解进行转移，从 $O(n^2)$ 优化到了 $O(n\log n)$ ，就是有一个不小的突破。

#include <bits/stdc++.h> 
using namespace std;
const int N=25010;
const int INF=0x3f3f3f;
int n,T;
struct node{
    int l,r;
    node(){}
    node(int a,int b):l(a),r(b){}
    bool operator < (const node t)const{
        if(l==t.l) return r<t.r;
        return l<t.l;
    }
}a[N];
struct heap_node{
    int id,val;
    heap_node(){}
    heap_node(int a,int b):id(a),val(b){}
    bool operator <(const heap_node t)const{
        return val>t.val;
    }
};
priority_queue<heap_node> heap;
int f[1001000];
int main(){
    scanf("%d%d",&n,&T);
    for(int i=1;i<=n;i++){
        int l,r;scanf("%d%d",&l,&r);
        a[i]=node(l,r);
    }
    sort(a+1,a+n+1);
    memset(f,INF,sizeof(f));
    f[0]=0;
    heap.push(heap_node(0,0));
    for(int i=1;i<=n;i++){
        heap_node tt;
        tt=heap.top();
        while(!heap.empty()&&(heap.top().id<a[i].l-1)){
            heap.pop();tt=heap.top();
        }
        if(heap.empty()) break;
        f[a[i].r]=min(tt.val+1,f[a[i].r]);
        heap.push(heap_node(a[i].r,tt.val+1));
    }
    printf("%d",f[T]<INF?f[T]:-1);
    
}

总结：
其实你会发现，数据结构优化其实有点类似于贪心算法，只不过是在进行决策的时候利用了贪心的性质或者数据结构的处理和优化从而减少了得到最优的决策的枚举次数。本身并不是很难想。

单调队列优化

这个优化方式是非常常见的，利用的就是转移方程的单调性来减少转移决策的枚举。用到的工具就是上面提到的双端队列，~~以及你聪明的大脑~~。具体使用还是要做题来感受一下啊…

【例题2】Fence（POJ1821）

A team of k (1 <= K <= 100) workers should paint a fence which contains N (1 <= N <= 16 000) planks numbered from 1 to N from left to right. Each worker i (1 <= i <= K) should sit in front of the plank Si and he may paint only a compact interval (this means that the planks from the interval should be consecutive). This interval should contain the Si plank. Also a worker should not paint more than Li planks and for each painted plank he should receive Pi $ (1 <= Pi <= 10 000). A plank should be painted by no more than one worker. All the numbers Si should be distinct.

Being the team’s leader you want to determine for each worker the interval that he should paint, knowing that the total income should be maximal. The total income represents the sum of the workers personal income.

Write a program that determines the total maximal income obtained by the K workers.

先按照一般的做法来做，令 $F[i,j]$ 表示前 $i$ 个工匠刷前 $j$ 个木板。

则显然有方程 $F[i,j]_{j\leq S_i}=max\begin{cases} F[i,j-1]\\ F[i-1,j]\\ \max_{j-L_i\leq k\leq S_i-1}\left\{ F[i-1,k]+P_i*(j-k)\right\} \end{cases}$

针对第三个情况，我们发现对于当前层的 $i,j$ ， $P_i*j$ 为定值，那么可以把第三个式子进行变形
$F[i,j]=P_i*j+max\left\{ F[i-1,k]-P_i*k\right\}$
其中枚举条件如上。

那么显然，对于同一个 $i$ 下的决策 $k_1,k_2(k_1\leq k_2)$ ，如果存在
$F[i-1,k_1]-P_i*k_1 \leq F[i-1,k_2]-P_i*k_2$

那么意味着 $k_2$ 的决策必定比 $k_1$ 要好，在当前层的 $i$ 的情况下， $k_2$ 直接将 $k_1$ 覆盖掉了，那么在转移的时候就直接忽略掉 $k_1$

然后就利用双端队列进行维护这个就可以了。

概括一下操作：

当前层枚举转移的决策，更优的决策将队尾已有的较为差的决策覆盖，即队尾差的全部弹出，再讲当前决策插入进去
枚举决策转移对象 $j$ ，由于 $j$ 也具有单调递增的性质，那么就可以将队首不合法的决策剔除
队首就是你要找的最优解。

但是很多人并没有把为什么队首就是最优解这个问题讲清楚。

首先可以知道对于原始方程当中的所有决策来说，
$F[i-1,k_1]-P_i*k_1 \leq F[i-1,k_2]-P_i*k_2$

那么对于一个 $F[i,j]$ ，所转移的对象一定是单个的（有多个也是计算结果相同的，对于答案并无影响），而唯一的一个就是在合法范围内的（队列当中的顺序是递增的，而你在第二步的时候就已经把不合法的去除了），那么这个就是对于当前的 $i,j$ 的唯一的转移状态。

然后手动算一下复杂度，你会发现在最外层是枚举的 $i$ ，内部先做一次状态插入，然后在枚举每一个的状态转移。时间复杂度就是 $O(MN)$ 。

空间上优化的话就会发现每一个状态之和上一个状态有关，所以滚一下就好了orz。

贴个代码，没有空间优化orz

#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int MOD=1e9+7;
const int N=16010;
const int M=110;
inline void read(int &x){
    x=0;int mm=1; char ch=getchar();
    while((ch>'9'||ch<'0')&&ch!='-') ch=getchar();
    if(ch=='-') mm=-1,ch=getchar();
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
    x=x*mm;
}
inline void read(LL &x){
    x=0;LL mm=1; char ch=getchar();
    while((ch>'9'||ch<'0')&&ch!='-') ch=getchar();
    if(ch=='-') mm=-1,ch=getchar();
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
    x=x*mm;
}
struct node{
    int l,p,s;
    bool operator <(const node t)const{
        return s<t.s;
    }
}a[M];
int n,m;
int f[M][N];
int get_val(int t1,int t2){
    return f[t1-1][t2]-a[t1].p*t2;
}
deque<int> q;
int main(){
    while(cin>>n>>m){
        memset(f,0,sizeof(f));
        for(int i=1;i<=m;i++){
            read(a[i].l),read(a[i].p),read(a[i].s);
        }
        sort(a+1,a+m+1);
        for(int i=1;i<=m;i++){
            q.clear();
            for(int k=max(0,a[i].s-a[i].l);k<=a[i].s-1;k++){
                while(!q.empty()&&(get_val(i,q.back())<=get_val(i,k)))  q.pop_back();
                q.push_back(k);
            }
            for(int j=1;j<=n;j++){
                f[i][j]=max(f[i-1][j],f[i][j-1]);
                if(j>=a[i].s){
                    while(!q.empty()&&q.front()<j-a[i].l) q.pop_front();
                    if(!q.empty())f[i][j]=max(f[i][j],get_val(i,q.front())+a[i].p*j);
                }
            }
        }
        cout<<f[m][n]<<'\n';
    }
    
}

【例题3】Cut the Sequence（POJ3017）

Given an integer sequence { an } of length N, you are to cut the sequence into several parts every one of which is a consecutive subsequence of the original sequence. Every part must satisfy that the sum of the integers in the part is not greater than a given integer M. You are to find a cutting that minimizes the sum of the maximum integer of each part.

还是从正常的开始做起，令 $F[i]$ 表示到第 $i$ 的最小值，可以写出转移方程
$F[i]=\min_{(0\leq j<i,\sum_{t=i}^{j}{A_t}\leq M)}\left\{ F[j]+\max_{j+1\leq k \leq i}\left\{ A_k\right\} \right\}$

开始考虑优化，区间最大值是静态问题，可以考虑用ST做法解决，时间复杂度是 $O(nlogn)$ 。

但还是要从当前节点向前枚举 $j$ 来寻找转移状态。

寻找规律发现

$\sum_{k=j}^{i}{A_k}>M$ 。就是所找寻的区间要在合法范围内尽可能的大。
$A_j=\max_{j\leq k \leq i}\left\{A_k\right\}$ ，就是说在所选择的这个区间内，最大值一定是在开头。

满足其中一个规律就可以了

第一个规律比较好想。因为最大的几个值一定是会被加进去的，所以尽可能地减少选择的区间从而减少最终的结果。而减少区间的做法就是尽力寻找满足第一个条件的区间。

第二个其实比较难想到，如果当前这个不是最大值，同时整个和还不是最大的，那么就是后面的一个元素还可以加到我这个区间里面，那就让他加啊！那如果不满足上一个条件，这个数就一定是区间内的最大值。

证明一下

假设两个条件都不成立，而在 $j$ 时取得最优决策，即
$A_j<\max_{j\leq k \leq i}\left\{A_k\right\},\sum_{k=j}^{i}{A_k}\leq M$
那么可以知道
$\max_{j\leq k \leq i}\left\{A_k\right\} = \max_{j+1\leq k \leq i}\left\{A_k\right\}$
由于 $F[i]$ 具有单调性（从前往后坐肯定越来越大），那么就可以得出
$F[j-1]\leq F[j]$
上面两式加一加，就会发现
$F[j-1]+\max_{j\leq k \leq i}\left\{A_k\right\} \leq F[j]+\max_{j+1\leq k \leq i}\left\{A_k\right\}$
这个式子的意思就是 $j-1$ 的决策要更优，那么和上面的条件矛盾，那么在两个当中必然有一个是成立的

第一个条件比较好处理，在读进来的时候记录对于每一个 $i$ 满足的的 $C[i]$ 就可以了

第二个条件比较难搞，就要用到我们的单调队列了。由于插进来的 $j$ 具有单调递增的性质 $(j_1\leq j_2)$ ，那么有满足 $A_1 \leq A_2$ 的时候 $A_1$ 就是没用的决策，被 $A_2$ 覆盖。

但是，虽然在单调队列当中的 $A_i$ 具有单调的性质，但是所形成的 $F[j]+\max_{j+1\leq k \leq i}\left\{ A_k\right\}$ 并没有单调性。那就把上面说的东西结合一下，拿一个堆来进行维护 $F[j]+\max_{j+1\leq k \leq i}\left\{ A_k\right\}$ ，利用懒惰删除法标记转移的节点是否在队列当中然后来判断在堆当中的是否有效

复杂度大概就是 $O(nlogn)$

代码没用堆优化，暴力扫一把队列当中的元素也可以达到目的orz。

#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <cstdio>
#include <queue>
#define LL long long
#define INF 0x3f3f3f
using namespace std;
const int MOD=1e9+7;
const int N=1e5+100;
const int M=110;
inline void read(int &x){
    x=0;int mm=1; char ch=getchar();
    while((ch>'9'||ch<'0')&&ch!='-') ch=getchar();
    if(ch=='-') mm=-1,ch=getchar();
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
    x=x*mm;
}
inline void read(LL &x){
    x=0;LL mm=1; char ch=getchar();
    while((ch>'9'||ch<'0')&&ch!='-') ch=getchar();
    if(ch=='-') mm=-1,ch=getchar();
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
    x=x*mm;
}
int n;
LL m,f[N];
int a[N];
int c[N];
bool visited[N];
struct deque{
    LL aa[N];
    int head,tail;
    void init(){
        head=1,tail=0;
    }
    bool empty(){
        return head==tail+1;
    }
    int back(){
        return aa[tail];
    }
    int front(){
        return aa[head];
    }
    void pop_back(){
        tail--;
    }
    void pop_front(){
        head++;
    }
    void push_back(int x){
        aa[++tail]=x;
    }
}q;
int main(){
    read(n),read(m);
    int l=1;LL s=0;
    for(int i=1;i<=n;i++){
        read(a[i]);
        if(a[i]>m){
            printf("-1");
            return 0;
        }
        s+=a[i];
        while(s>m) s-=a[l++];
        c[i]=l;
    }
    q.init();
    q.push_back(1);
    f[1]=a[1];
    for(int i=2;i<=n;i++){
        while(!q.empty()&&a[q.back()]<=a[i]) q.pop_back();
        while(!q.empty()&&q.front()<c[i]) q.pop_front();
        q.push_back(i); 
        f[i]=f[c[i]-1]+1ll*a[q.front()];
        for(int j=q.head;j<=q.tail-1;j++){
            f[i]=min(f[i],f[q.aa[j]]+1ll*a[q.aa[j+1]]);
        }
    }
    cout<<f[n];

总结：
单调队列优化相比较于数据结构优化，更加具有难度，对你的方程和你的数学处理能力具有一定的能力，但效率也有了飞跃的提高。代码实现上并没有什么难度。
但在实战当中，当你没有办法证明一个猜想的时候，对于一些大数据还是要能骗分就骗分吧…

斜率优化

这个也是利用了数据的单调性，也需要用到单调队列，但是相对于单调队列本身的优化，变形的形式就更加的多并且复杂了。维护的是数据之间的某一种斜率乘法/除法关系。对于你对数据的敏感程度要求会更加高。

【例题4】任务安排1（洛谷2365）

N( $1\leq N\leq 5000$ )个任务排成一个序列在一台机器上等待完成（顺序不得改变），这N个任务被分成若干批，每批包含相邻的若干任务。从时刻0开始，这些任务被分批加工，第i个任务单独完成所需的时间是Ti。在每批任务开始前，机器需要启动时间S，而完成这批任务所需的时间是各个任务需要时间的总和（同一批任务将在同一时刻完成）。每个任务的费用是它的完成时刻乘以一个费用系数Fi。请确定一个分组方案，使得总费用最小。

例如：S=1；T={1,3,4,2,1}；F={3,2,3,3,4}。如果分组方案是{1,2}、{3}、{4,5}，则完成时间分别为{5,5,10,14,14}，费用C={15,10,30,42,56}，总费用就是153。

这是非常好的一道题，也是从正常的操作入手（通过之前的几个例题发现，所有的优化都需要先进行基础的建模和方程构建，不可能凭空进行一个最优的处理）

令 $F[i,j]$ 表示前 $i$ 个任务分成 $j$ 份的最小费用。 $sumT[i],sumC[i]$ 表示时间和费用的前缀和，那么可以得出方程
$F[i,j]=\min_{}\left\{ F[k,j-1]+(S*j+sumT)*(sumC[i]-sumC[k])\right\}$

显然这个算法需要枚举三层，是一个 $O(n^3)$ 的算法，再看看数据，果断放弃。

换一个思路，令 $F[i]$ 表示前 $i$ 个的最小费用。得出方程：
$F[i]=\min_{}\left\{ F[j]+sumT[i]*(sumC[i]-sumC[j])+S*(sumC[N]-sumC[j])\right\}$
由于当前这个 $i$ 分为一组，不管怎么样，后面的结果都要加上 $S*(sumC[N]-sumC[j])$ 的一部分，所以就干脆前面解决掉，叫做费用提前计算的思想

#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <cstdio>
#include <queue>
#define LL long long
#define INF 0x3f3f3f
using namespace std;
const int MOD=1e9+7;
const int N=5010;
const int M=110;
inline void read(int &x){
    x=0;int mm=1; char ch=getchar();
    while((ch>'9'||ch<'0')&&ch!='-') ch=getchar();
    if(ch=='-') mm=-1,ch=getchar();
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
    x=x*mm;
}
inline void read(LL &x){
    x=0;LL mm=1; char ch=getchar();
    while((ch>'9'||ch<'0')&&ch!='-') ch=getchar();
    if(ch=='-') mm=-1,ch=getchar();
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
    x=x*mm;
}
int n,s;
int sumc[N],sumt[N];
int f[N];
int main(){
    read(n);read(s);
    for(int i=1;i<=n;i++){
        int t1,t2;
        read(t1),read(t2);
        sumt[i]=sumt[i-1]+t1;
        sumc[i]=sumc[i-1]+t2;
    }
    memset(f,INF,sizeof(f));
    f[0]=0;
    for(int i=1;i<=n;i++){
        for(int j=0;j<i;j++){
            f[i]=min(f[i],f[j]+sumt[i]*(sumc[i]-sumc[j])+s*(sumc[n]-sumc[j]));
        }
    }
    cout<<f[n];
    
}

【例题4】任务安排2

题目如任务安排1，但是我将数据修改到 $1\leq N\leq 3*10^5,1\leq S,T_i,C_i \leq 512$

还是上面的那个式子 $F[i]=\min_{}\left\{ F[j]+sumT[i]*(sumC[i]-sumC[j])+S*(sumC[N]-sumC[j])\right\}$

我们将式子进行变形，变成
$F[i]=\min_{0\leq j<i}\left\{F[j]-(sumT[i]+S)*sumC[j]\right\}+sumT[i]*sumC[i]+S*sumC[N]$

把 $min$ 函数去掉之后继续变形就变成
$F[j]=(sumT[i]+S)*sumC[j]+F[i]-sumT[i]*sumC[i]+S*sumC[N]$
后面整体的 $F[i]-sumT[i]*sumC[i]+S*sumC[N]$ 可以看做是常量，本来就是要让 $F[i]$ 最小

那么就可以认为这个式子是一个以 $(sumT[i]+S)$ 作为斜率的直线，坐标系内的 $(sumC[j],F[j])$ 都是一些点。

那么就变成了计算机模拟数学的线性规划了

在这里插入图片描述

显然你会发现，如果是数学的线性规划，就只需要在最边界上的点进行枚举就可以了，这样子你所进行选择的点就形成了一个凸包（上凸或下凸），可以利用单调队列进行维护

那么就可以在单调队列当中进行检查，如果斜率满足 $\frac{F[q[l+1]]-F[q[l]]}{sumC[q[l+1]]-sumC[q[l]]}\leq S+sumT[i]$
就将队首的元素进行出队，从图中可以明显的发现这个事实，队首的元素不是最优决策点。

然后再根据 $\frac{F[i]-F[q[r]]}{sumC[i]-sumC[q[r]]}\leq\frac{F[q[r]]-F[q[r-1]]}{sumC[q[r]]-sumC[q[r-1]]}$
即新的斜率比原来的斜率小，那么原来队尾的节点就在新的凸包范围内了。

在这里插入图片描述

然后再将新的节点塞到队尾就可以了。

#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <cstdio>
#include <queue>
#define LL long long
#define INF 0x3f3f3f
using namespace std;
const int MOD=1e9+7;
const int N=300100;
const int M=110;
inline void read(int &x){
    x=0;int mm=1; char ch=getchar();
    while((ch>'9'||ch<'0')&&ch!='-') ch=getchar();
    if(ch=='-') mm=-1,ch=getchar();
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
    x=x*mm;
}
inline void read(LL &x){
    x=0;LL mm=1; char ch=getchar();
    while((ch>'9'||ch<'0')&&ch!='-') ch=getchar();
    if(ch=='-') mm=-1,ch=getchar();
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
    x=x*mm;
}
int n,s;
int q[N],l,r;
LL sumc[N],sumt[N];
LL f[N];
int main(){
    read(n);read(s);
    for(int i=1;i<=n;i++){
        int t1,t2;
        read(t1),read(t2);
        sumt[i]=sumt[i-1]+t1;
        sumc[i]=sumc[i-1]+t2;
    }
    l=r=1;
    q[1]=0;
    f[0]=0;
    for(int i=1;i<=n;i++){
        while(l<r&&(f[q[l+1]]-f[q[l]])<=(s+sumt[i])*(sumc[q[l+1]]-sumc[q[l]])) l++;
        f[i]=f[q[l]]-(s+sumt[i])*sumc[q[l]]+sumt[i]*sumc[i]+s*sumc[n];
        while(l<r&&(f[q[r]]-f[q[r-1]])*(sumc[i]-sumc[q[r]])>=(f[i]-f[q[r]])*(sumc[q[r]]-sumc[q[r-1]])) r--;
        q[++r]=i;
    }
    cout<<f[n];
    
}

【例题5】任务安排3

题目如任务安排1，但是我将数据修改到 $1\leq N\leq 3*10^5,1\leq S,C_i\leq 512,-512\leq T_i\leq512$

显然这里这里的 $sumC$ 仍旧具有单调性，但是由于 $T_i$ 存在负值， $sumT$ 的单调性被打破了。 $S+sumT[i]$ 也不一定只是正值，所以要保留整个凸壳，然后二分查找最优解。

代码我就不打了（这个我没打过…）大家自己体会吧…

四边形不等式

这个东西其实优化条件比较难，但用起来非常好用…本身也非常的有意思。

定义
令函数 $w(x,y)$ 是一个二元函数，并且满足 $a\leq b\leq c\leq d$ 的情况下， $w(a,c)+w(b,d)\leq w(a,d)+w(b,c)$ 恒成立，那么满足四边形不等式。

简单的画个图就是

在这里插入图片描述

定理1（引理）
如果函数 $w(x,y)$ 当中任意 $a,b$ 满足 $a<b$ 都有 $w(a,b)+w(a+1,b+1)\leq w(a,b+1)+w(a+1,b)$ ，那么满足四边形不等式。

这个证明其实很简单，套定义也是可以的。

一维线性DP优化

单调性定义
假设对于 $F[i]=\min_{0\leq j <i}\left\{ F[j]+val(j,i)\right\}$ ， $p[i]$ 是 $i$ 取到的决策最小值的位置，并且 $p[i]$ 单调不减，那么称 $F[i]$ 具有单调性

定理2（决策单调性）

在方程 $F[i]=\min_{0\leq j <i}\left\{ F[j]+val(j,i)\right\}$ 的转移方程中，若函数 $val(j,i)$ 满足四边形不等式，那么 $F[i]$ 具有单调性

证明：

令 $i\in[1,N],j\in[0,p[i]-1]$ ，那么根据 $p[i]$ 具有最优性，可以得出

$F[p[i]]+val(p[i],i)\leq F[j]+val(j,i)$
令 $i'\in[i+1,N]$ ，由于 $val$ 函数满足四边形不等式，那么有
$j<p[i]<i<i'$
$val(j,i)+val(p[i],i')\leq val(j,i')+val(p[i],i)$
移项之后可以得到：
$val(p[i],i')-val(p[i],i)\leq val(j,i')-val(j,i)$
与原始方程左右相加，可以得到：
$F[p[i]]+val(p[i],i')\leq F[j]+ val(j,i')$

这个式子的意思是，以 $p[i]$ 作为 $i'$ 的决策转移点比 $j$ 更优，而由于 $j<p[i]$ ，那么 $p[i]\leq p[i']$ 所以具有单调性

当 $F$ 具有单调性的时候， $p$ 也具有单调性，那么我们就可以考虑对 $p$ 进行优化，从而减少枚举转移状态，优化时间复杂度。

考虑 $p$ 数组，由于决策单调，每求出一个 $F[i]$ 就去寻找可以作为哪些 $F[i']$ 的决策转移对象，寻找这一个位置就可以了。在这一段位置之前， $p$ 所存的决策都比 $i$ 差，之后的doubi $i$ 好。我们要做的就是找到这些位置然后把这些变成 $i$ 。

显然，维护数组太慢了，所以可以维护一个队列 ~~（对！又是单调队列）~~ 队列当中记录三元组 $(j,l,r)$ ，分别表示决策和左右端点就可以了。更新的时候就只要判断队尾是否比 $i$ 更优，不是弹出，找到一个包含 $i$ 的左右不同决策的就进行二分查找就可以了。

然后没有必要在队列当中保留转移位置小于 $p[1,i-1]$ 的了，一方面是因为已经进行了状态转移了，另一方面由于单调性，也不会被再用到了。这样也能够一下子就是队头是最优决策。

总结操作就是以下几步：

检查队头：若队头的右端点小于 $i$ 就直接弹出，否则如果左端点直接等于 $i$ 。（单调性）
取队头做最优决策。
插入新的队尾（这个就按照上面说的做就好了）。

【例题5】诗人小G（洛谷P1912）

小G是一个出色的诗人，经常作诗自娱自乐。但是，他一直被一件事情所困扰，那就是诗的排版问题。

一首诗包含了若干个句子，对于一些连续的短句，可以将它们用空格隔开并放在一行中，注意一行中可以放的句子数目是没有限制的。小G给每首诗定义了一个行标准长度（行的长度为一行中符号的总个数），他希望排版后每行的长度都和行标准长度相差不远。显然排版时，不应改变原有的句子顺序，并且小G不允许把一个句子分在两行或者更多的行内。在满足上面两个条件的情况下，小G对于排版中的每行定义了一个不协调度, 为这行的实际长度与行标准长度差值绝对值的P次方，而一个排版的不协调度为所有行不协调度的总和。

小G最近又作了几首诗，现在请你对这首诗进行排版，使得排版后的诗尽量协调（即不协调度尽量小），并把排版的结果告诉他。

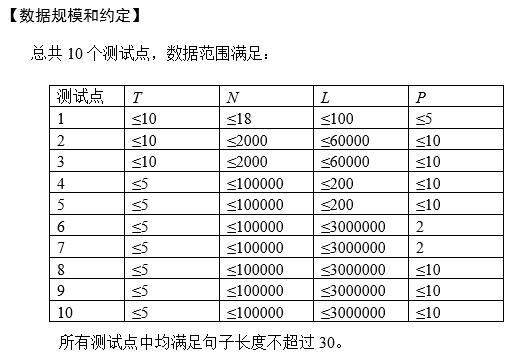
输入包含多组数据。
第一行包含一个整数T，表示诗的数量，接下来是T首诗，这里一首诗即为一组数据。每组数据的第一行包含三个由空格分隔的正整数N、L、P，其中N表示这首诗句子的数目，L表示这首诗的行标准长度，P的含义见问题描述。从第2行开始，每行为一个句子，句子由英文字母、数字、标点符号等符号组成(ASCII码33~127, 但不包含 ‘-’)。

于每组测试数据，若最小的不协调度不超过10^18，则第一行为一个数，表示不协调度。

在这里插入图片描述

令 $F[i]$ 表示前 $i$ 句诗的最小不协调度，记 $a[i]$ 为第 $i$ 句诗的长度， $sum[i]$ 为前 $i$ 句诗的总长度。
$F[i]=\min_{0\leq j<i}\left\{ F[j]+ |sum[i]-sum[j]+i-j-1|^p \right\}$

显然这个 $O(n^2)$ 的枚举加上高次快速幂判断果断会超时，但是高次项不能够保证单调性，那考虑四边形不等式优化。

这里的 $val(j,i)=|sum[i]-sum[j]+i-j-1|^p$ ，要证明对于任意的 $j<i$ ， $val(j,i)+val(j+1,i+1)\leq val(j,i+1)+val(j+1,i)$
那么只需要证明 $val(j,i)- val(j,i+1)\leq val(j+1,i)-val(j+1,i+1)$
令
$u=(sum[i]+i)-(sum[j]+j)-(L+1)$ $v=(sum[i]+i)-(sum[j+1]+j+1)-(L+1)$

那么显然只需要把上面这个式子展开，变成
$|u|^p-|u+(a[i+1]+1)|^p\leq |v|^p-|v+(a[i+1]+1)|^p$
证明这个就可以了。

但证明这个需要用到导数知识，还要分类讨论，在这里不一一赘述了（反正它成立你大概也能够猜到吧…）

然后就可以用四边形不等式做了。

注意数据会爆longlong

#include <bits/stdc++.h>
#define LL long double
using namespace std;
int T;
const int N=1e5+10;
int n,l,p;
LL sum[N],f[N];
struct node{
	int val,l,r;
};
deque<node> q;
LL quick(LL x){
	if(x<0) x=-x;
    LL t=1;
    for(int i=1;i<=p;i++) t*=x;
    return t;
}
LL cal(int j,int i){
	return f[j]+quick(sum[i]-sum[j]+(LL)i-(LL)j-1-(LL)l);
}
int main(){
	scanf("%d",&T);
	while(T--){
		scanf("%d%d%d",&n,&l,&p);
		char s[50];
		for(int i=1;i<=n;i++)scanf("%s",s),sum[i]=sum[i-1]+(LL)strlen(s);
		q.clear();
		memset(f,0,sizeof(f));
		q.push_back((node){0,0,n});
		for(int i=1;i<=n;i++){
			if(!q.empty()&&q[0].r<i) q.pop_front();
			int bbt=q[0].val;
			f[i]=cal(bbt,i);
			if(q.empty()||cal(i,n)<=cal(q.back().val,n)){
				while(!q.empty()&&cal(i,q.back().l)<=cal(q.back().val,q.back().l)) q.pop_back();
				if(q.empty()) {	q.push_back((node){i,i,n});
				}else{
					int lt=q.back().l,rt=q.back().r,mid;
					while(lt<=rt){
						mid=(lt+rt)>>1;
						if(cal(i,mid)>cal(q.back().val,mid)) lt=mid+1;
						else rt=mid-1;
					}
					q.back().r=lt-1;
					q.push_back((node){i,lt,n});
				}
			}
		}
		if(f[n]<0) f[n]=-f[n];
		if(f[n]>1e18) printf("Too hard to arrange\n");
        else printf("%lld\n",(long long)(f[n]));
		for(int i=1;i<=20;i++) putchar('-');
        if(T!=0) putchar('\n');
	}
}

总结：显然四边形不等式证明起来和想起来没有之前两个简单快捷，代码量其实相比之前的也有点大，但总体来说还是有着不小的优化。

二维区间DP优化

这个我不会，等着更新吧！

浅谈DP优化

数据结构优化

【例题1】Cleaning Shifts（POJ2376）

单调队列优化

【例题2】Fence（POJ1821）

【例题3】Cut the Sequence（POJ3017）

斜率优化

【例题4】任务安排1（洛谷2365）

【例题4】任务安排2

【例题5】任务安排3

四边形不等式

一维线性DP优化

【例题5】诗人小G（洛谷P1912）

二维区间DP优化

猜你喜欢