Variational Autoencoder: Basic Concept

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/zhangxb35/article/details/78089070

The neural network perspective

传统的 Autoencoder 结构如下图：

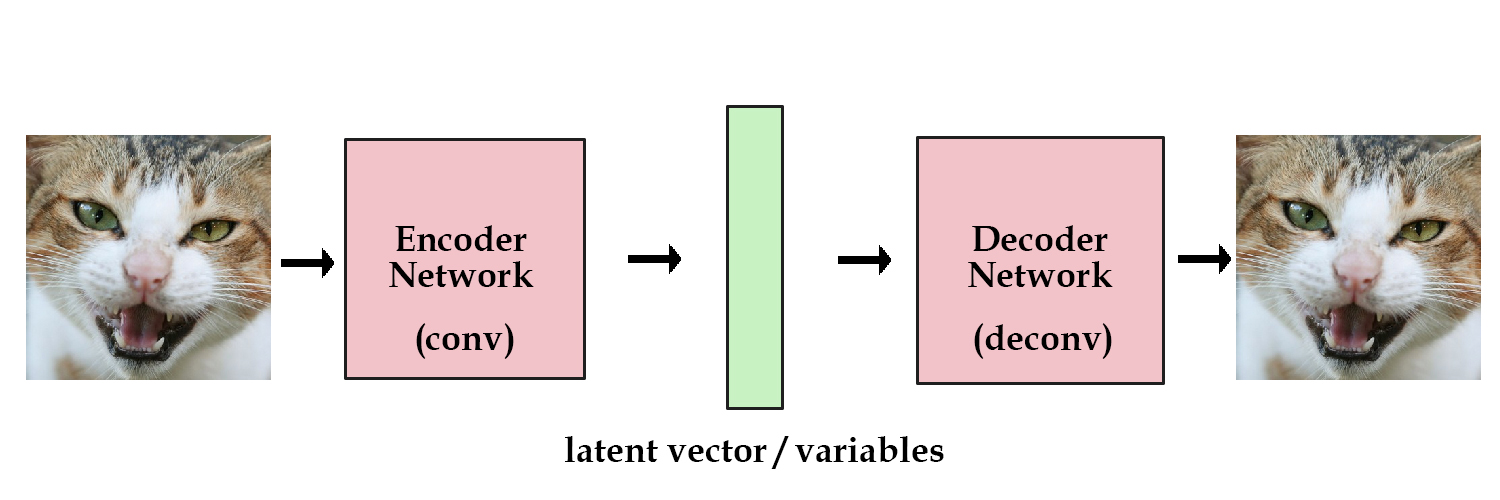
但是这种结构没法生成新数据，只能做数据压缩。怎么改进呢？可以考虑加一个正则项，让隐变量趋近一个单位高斯分布。

generation_loss = mean(square(generated_image - real_image))  
latent_loss = KL-Divergence(latent_variable, unit_gaussian)  
loss = generation_loss + latent_loss  

其中两个高斯分布的 KL divergence 可以套公式计算如下，

# z_mean and z_stddev are two vectors generated by encoder network
latent_loss = 0.5 * tf.reduce_sum(tf.square(z_mean) + \ 
            tf.square(z_stddev) - tf.log(tf.square(z_stddev)) - 1,1)  

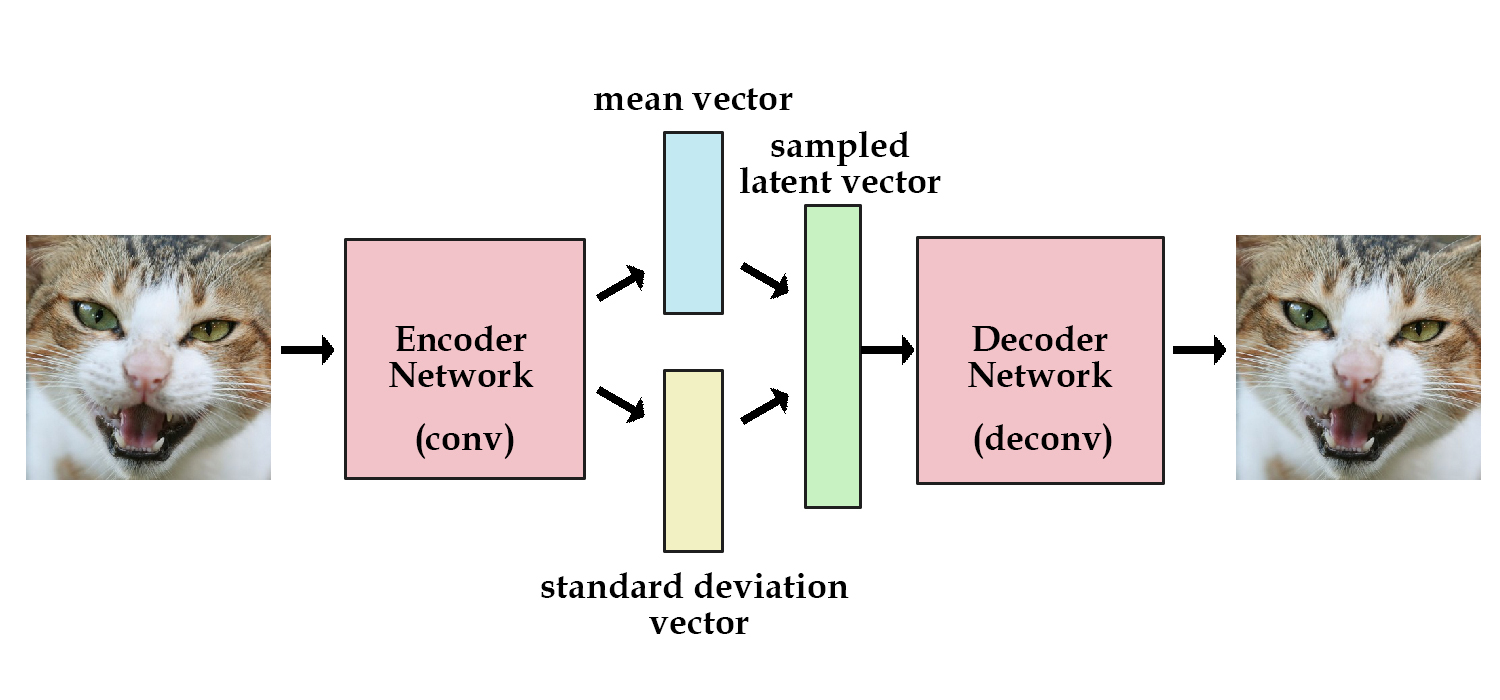
值得一提的是，encoder 不是直接生成隐变量 $z$ 的分布，而是先假设隐变量服从一个高斯分布，让 encoder 生成高斯分布的均值和方差。代码是这样的

samples = tf.random_normal([batchsize,n_z],0,1,dtype=tf.float32)  
sampled_z = z_mean + (z_stddev * samples)

下面用公式形式化地描述上面的过程，用 $q_\theta(z|x)$ 表示 encoder，也叫 Inference Network，是从样本中得到隐变量；用 $p_\phi(x|z)$ 表示 decoder，也叫 Generative Network. 其中 $\theta, \phi$ 是神经网络的参数，即权重和偏置。

那么对单个样本 $x_i$ 的损失为

$$L_i(\theta, \phi)= -\mathbb{E}_{z \sim q_\theta(z|x_i)}[\log p_\phi(x_i|z)] + KL(q_\theta(z|x_i) \| p(z))$$

前者是重构损失，用对数是因为要极大化整体训练集的对数似然函数；后者是 KL divergence 的正则项。$p(z) \sim \mathcal{N}(0, I)$

假设 encoder 得到的高斯分布的均值为 $\mu(x)$，方差是 $\Sigma(x)$，而 $p(z)$ 服从标准正态分布，即 $p(z) \sim \mathcal{N}(0, I)$，其中 $I$ 是单位矩阵。那么 KL divergence 计算如下，

$$KL[\mathcal{N}(\mu(x), \Sigma(x)) \| \mathcal{N}(0, I)] = \frac12(\mathrm{tr}(\Sigma(x)) + (\mu(x))^\top(\mu(x)) - k - \log \det(\Sigma(x)))$$

---

The probability model perspective

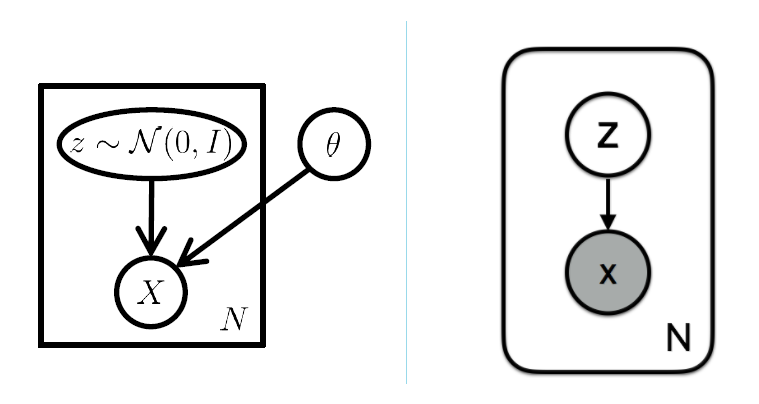
如果是概率图模型的角度，有隐变量 $z$ 和观察变量 $x$，那么联合概率分布是

$$p(x,z) = p(z) p(x|z)$$ 其中隐变量符合分布 $z_i \sim p(z)$，即先验概率；观察变量符合分布 $x_i \sim p(x|z)$，即似然概率。可以从图模型的表示中看出，变量 $x$ 条件相关于隐变量 $z$，所以我们的数据都可以通过先从 $p(z)$ 中抽样，然后从 $p(x|z)$ 中生成。

概率图模型可以分成 Representation, Learning 和 Inference 三个任务，Representation 就是如何建立模型（有向图还是无向图），可以用 plate notation 表示；Learning 就是学习图模型里的参数，可以用比如 EM 算法来求解隐变量，于是求得联合概率分布；Inference 则是从联合概率分布中求得条件概率分布。比如我们对隐变量 $z$ 感兴趣，想得到 $p(z|x)$ 的分布（其实就是 encoder 想做的，根据 $x$ 生成对应的 $z$）。可以用贝叶斯公式展开，转化成后验概率，

$$p(z|x) = \frac{p(x|z)p(z)}{p(x)}$$ 分子就是联合概率，上面已经讲过了，而分母 $p(x)$ 叫做 evidence，可以通过积分 $p(x) = \int_z p(x|z)p(z)dz$ 来计算。但是计算量是指数级别的，因此很难求，所以后验概率也相应的很难求。

变分推断（Variational Inference）的思路是这样，考虑用一个简单一些的分布 $q_\lambda(z|x)$ 来估计后验概率 $p(z|x)$，计算 $p, q$ 的 KL divergence，并最小化，就可以拉近这两个分布之间的距离。分布 $q_\lambda$ 比如可以用高斯分布，那么参数 $\lambda = (\mu, \sigma^2)$.

怎么理解 $q$ 和 $p$ 的关系呢？其实 $q$ 是 $p$ 的一个近似和逼近，即使不完全相等，即 KL 不为零，也没有关系。我们本来想要的也不是确切推断。本来如果从 $p(z|x)$ 中抽样出一个 $z$，都能够百分百重构出 $x$；而变分推断的初衷是说，如果从分布 $q(z|x)$ 抽样出一个隐变量 $z$，也能够以较大概率重构出 $x$，那么就差不多够用了。因此我们的优化目标就变成了

$$q^*(z|x) = \arg\min_\lambda KL(q_\lambda(z|x) \| p(z|x))$$ 即找一个能让 KL 距离最小的一个分布。

下面推导一下这个公式，

$$\begin{aligned} KL(q(z|x) \| p(z|x)) &= \mathbb{E}_{z \sim q_\lambda(z|x)}[\log q_\lambda(z|x) - \log p(z|x)] \\ &= \mathbb{E}_{z \sim q_\lambda(z|x)} \left [\log q_\lambda(z|x) - \log \frac{p(x|z) p(z)}{p(x)} \right ] \\ &= \mathbb{E}_{z \sim q_\lambda(z|x)} \left [\log q_\lambda(z|x) - \log p(x|z) - \log p(z) \right ] + \log p(x) \end{aligned}$$

后一项取负数后有个名字，叫做 Evidence Lower BOund，即

$$ELBO(\lambda) = - \mathbb{E}_{z \sim q_\lambda(z|x)} \left [\log q(z|x) - \log p(x|z) - \log p(z) \right]$$ 那么整个式子就重新简写成 $$\log p(x) = KL(q_\lambda(z|x) \| p(z|x)) + ELBO(\lambda)$$ 怎么理解这个公式呢？因为由 KL divergence 的定义可以知道，始终是非负的，所以数据的对数似然 $\log p(x)$ 函数有一个下限（lower bound）。由上式可以看出，如果以 $z$ 为自变量，因为待优化的参数 $\lambda$ 和 $p(x)$ 无关，所以最小化 KL 散度，就等价于最大化 $ELBO(\lambda)$。从 $\log p(x)$，其实就是在提高似然函数的下限。

我们继续来化简 ELBO，

$$\begin{aligned} ELBO(\lambda) &= - \mathbb{E}_{z \sim q(z|x)} \left [\log q_\lambda(z|x) - \log p(x|z) - \log p(z) \right] \\ &= \mathbb{E}_{z \sim q_\lambda(z|x)}[\log p(x|z)] - \mathbb{E}_{z \sim q_\lambda(z|x)}\left [\log \frac{q_\lambda(z|x)}{p(z)} \right ] \\ &= \mathbb{E}_{z \sim q_\lambda(z|x)}[\log p(x|z)] - KL(q_\lambda(z|x) \| p(z)) \end{aligned}$$ 由此可以发现，这里和前面讲过的损失函数是成负数关系，这里是最大化，前面是最小化。

细心的读者可以发现，其实两个式子还有一些不同的，那就是参数。ELBO 优化的参数仅仅是 $q_\lambda(z|x)$，也就是前面的 Inference Network $q_\theta(z|x)$，而 Generative Network $p_\phi(x|z)$ 该怎么优化呢？这里有个方法叫做 Inference EM，就是参考 EM 的做法，先优化 $q(z|x)$ 的参数，然后固定住当做常数，继续优化 $p(x|z)$ 的参数。两个都是最大化期望对数似然。

---

The Reparametrization Trick

最后再来聊聊为什么生成隐变量 $z$ 的时候要从一个高斯向量中去采样。如果直接生成隐变量会怎么样呢？考虑 $ELBO(\lambda)$ 的前一项，求解的期望其实是积分的形式，

$$\mathbb{E}_{z \sim q_\lambda(z|x)}[\log p(x|z)] = \int_{z \sim q_\lambda(z|x)} \log p(x|z) dz = \int_z q_\lambda(z|x) \log p(x|z) dz$$ 求解这个期望其实是分成了两步。第一步是 encoder 生成隐变量的分布，比如假设隐变量是多元高斯分布，那么 encoder 估计的是高斯分布的均值 $\mu(x)$ 和协方差矩阵 $\Sigma(x)$，此时得到了 $z$ 的分布 $\mathcal{N}(\mu(x), \Sigma(x))$。接着第二步，不断从这个分布中抽样出 $z$，计算出 $$\log p(x|z) - KL(q_\lambda(z|x) \| p(z))$$ 的值，然后去算损失和梯度。当然，按理说积分是要抽样无数次的，但是因为是随机梯度下降，所以只做一次抽样也没关系。

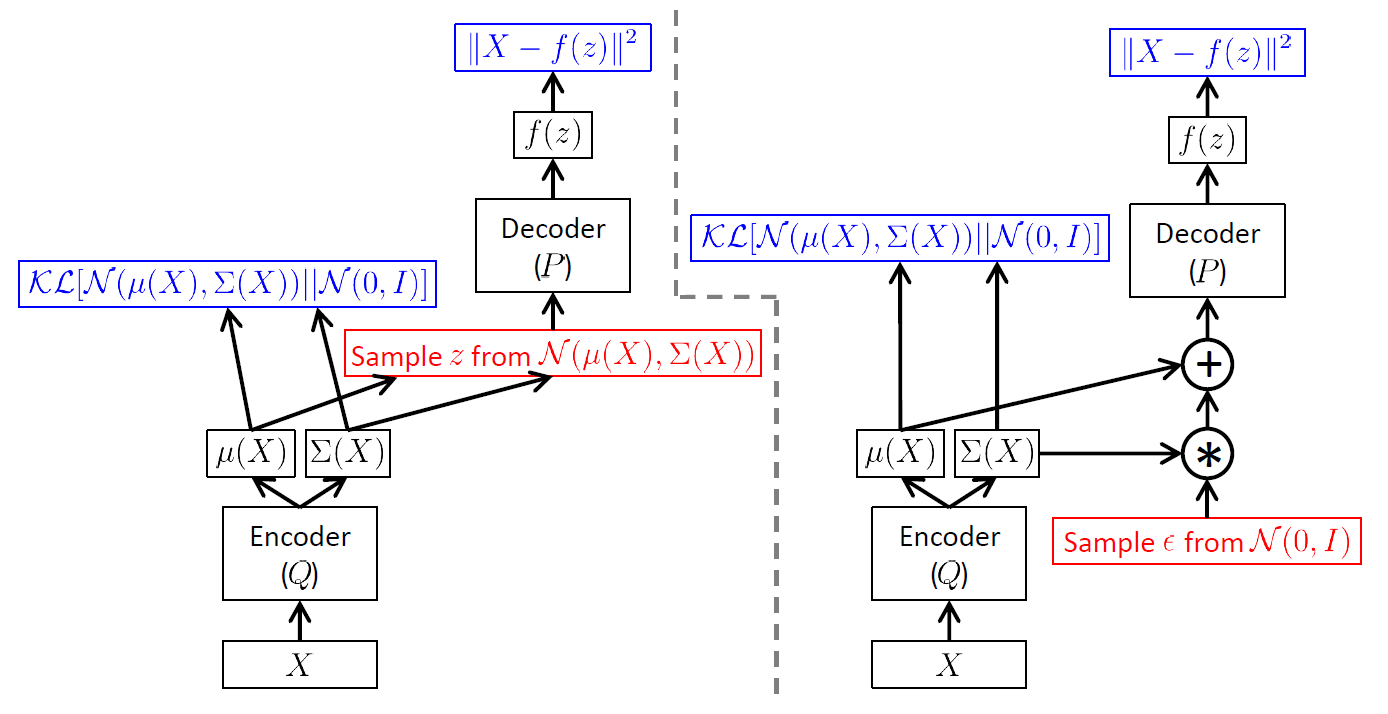
这里的问题是，网络中间出现了抽样（sampling）这个步骤，梯度回传到 $z$ 这里以后就断掉了，因为没法计算 $z$ 对网络 $q_\lambda(z|x)$ 的参数 $\lambda$ 的导数。VAE 中就采用了一个叫做重参数化的技巧（reparametrization trick），就是说把随机采样这个步骤抽离出来，用一个标准高斯分布 $\epsilon \sim \mathcal{N}(0, I)$ 来随机抽样，接着计算 $z = \mu(x) + \Sigma^\frac12(x) * \epsilon$，这样梯度就可以继续回传了。

Reference

• blog: Variational Autoencoders Explained
  
  • 有代码，浅显易懂
• blog: Tutorial-What is a variational autoencoder?
  
  • 讲的比较长，从 DL 和 GM 两个角度来理解问题。
• arxiv paper: Tutorial on Variational Autoencoders
  
  • 背后的原理和 intuition 讲的比较多。