part2
这节课主要讲的是生成式模型,那么与这个生成式模型相对于的就是我们上节课所讲那几个辨别式模型。所以生成式模型和辨别式模型的区别是什么呢。我先给出数学上的定义:
这是我们上节课线性回归所用的给定x下y的条件分布,即辨别式模型:
\[p(y|x;\theta )\]
那么生成式模型其实就是把条件反一下:
\[p(x|y;\theta )\]
那这到底是啥意思呢,比如说我们要判断一只动物是猫还是狗。辨别式模型做的就是从历史特征数据中学到一个模型。然后把猫和狗的特征带入到这个模型中,判断这个动物到底是猫还是狗。而生成式模型做的是从历史的特征数据中生成两个模型,一个是猫的模型,一个是狗的模型。把动物的特征放到这两个模型中判断哪个概率大。
但是这种形象的说法其实是很缺乏数学上的一些严谨性的,所以更具体的东西翻一下后面的参考。
这两个模型可以通过贝叶斯公式来统一:
\[p(y|x)=\frac{p(x|y)p(y)}{p(x)}\]
由于我们只关心y离散值里面的结果哪个大,而不是关心具体的概率,所以分母的p(x)是可以直接去掉的。
最后我们可以把这个式子写成:
\[ \left.\begin{aligned} \arg \max p ( y | x ) & = \arg \max _ { y } \frac { p ( x | y ) p ( y ) } { p ( x ) } \\ & = \arg \max _ { y } p ( x | y ) p ( y ) \end{aligned} \right. \]
高斯判别分析
问题背景
还是回到之前二元分类的那个判断房子是一线还是二线城市的例子中来。
样本集描述:
\[(x,y)\in D, x\in R^n, y\in \{0,1\}\]
假设函数
回归一下part1中判别式模型中逻辑回归的假设函数为:
\[ h(x)=\arg \max _ { y } p ( y | x ) \]
通过上面的贝叶斯公式,我们知道了生成式模型的假设函数就为:
\[ h(x)=\arg \max _ { y } p ( x | y ) p ( y ) \]
所以我们接下来要求的就是构造这个p(x|y)和p(y)。
既然这个算法都叫做高斯判别分析了,所以我们选用多变量高斯分布构造p(x|y)。
多变量高斯分布的概率密度函数为:
\[ p ( x ; \mu ,\Sigma ) = \frac { 1} { ( 2\pi ) ^ { n / 2} | \Sigma | ^ { 1/ 2} } \exp \left( - \frac { 1} { 2} ( x - \mu ) ^ { T } \Sigma ^ { - 1} ( x - \mu ) \right) \]
\(\mu\)为均值向量,\(\Sigma\)为协方差矩阵。
我们假设y=1和y=0的模型只有均值向量不同,协方差是一样的,于是就有:
\[ \left.\begin{aligned} p(y) & \sim \text{ Bernoulli } ( \phi ) \\ p(x | y = 0)& \sim \mathcal { N } \left( \mu _ { 0} ,\Sigma \right) \\ p(x | y = 1)& \sim \mathcal { N } \left( \mu _ { 1} ,\Sigma \right) \end{aligned} \right. \]
我们要的p(x|y)和p(y)就都构造好了。展开来就是:
\[ \left.\begin{aligned} p ( y ) & = \phi ^ { y } ( 1- \phi ) ^ { 1- y } \\ p ( x | y = 0) & = \frac { 1} { ( 2\pi ) ^ { n / 2} | \Sigma | ^ { 1/ 2} } \exp \left( - \frac { 1} { 2} \left( x - \mu _ { 0} \right) ^ { T } \Sigma ^ { - 1} \left( x - \mu _ { 0} \right) \right) \\ p ( x | y = 1) & = \frac { 1} { ( 2\pi ) ^ { n / 2} | \Sigma | ^ { 1/ 2} } \exp \left( - \frac { 1} { 2} \left( x - \mu _ { 1} \right) ^ { T } \Sigma ^ { - 1} \left( x - \mu _ { 1} \right) \right) \end{aligned} \right. \]
误差衡量
跟之前一样,还是求对数似然最大:
\[ \left.\begin{aligned} \ell \left( \phi ,\mu _ { 0} ,\mu _ { 1} ,\Sigma \right) & = \log \prod _ { i = 1} ^ { m } p \left( x ^ { ( i ) } ,y ^ { ( i ) } ; \phi ,\mu _ { 0} ,\mu _ { 1} ,\Sigma \right) \\ & = \log \prod _ { i = 1} ^ { m } p \left( x ^ { ( i ) } | y ^ { ( i ) } ; \mu _ { 0} ,\mu _ { 1} ,\Sigma \right) p \left( y ^ { ( i ) } ; \phi \right) \end{aligned} \right. \]
求解问题
最终的结果就是:
\[ \phi = \frac { 1} { m } \sum _ { i = 1} ^ { m } 1\left\{ y ^ { ( i ) } = 1\right\} \]
\[ \mu _ { 0} = \frac { \sum _ { i = 1} ^ { m } 1\left\{ y ^ { ( i ) } = 0\right\} x ^ { ( i ) } } { \sum _ { i = 1} ^ { m } 1\left\{ y ^ { ( i ) } = 0\right\} } \]
\[ \mu _ { 1} = \frac { \sum _ { i = 1} ^ { m } 1\left\{ y ^ { ( i ) } = 1\right\} x ^ { ( i ) } } { \sum _ { i = 1} ^ { m } 1\left\{ y ^ { ( i ) } = 1\right\} } \]
\[ \Sigma = \frac { 1} { m } \sum _ { i = 1} ^ { m } \left( x ^ { ( i ) } - \mu _ { y ^ { ( i ) } } \right) \left( x ^ { ( i ) } - \mu _ { y ^ { ( i ) } } \right) ^ { T } \]
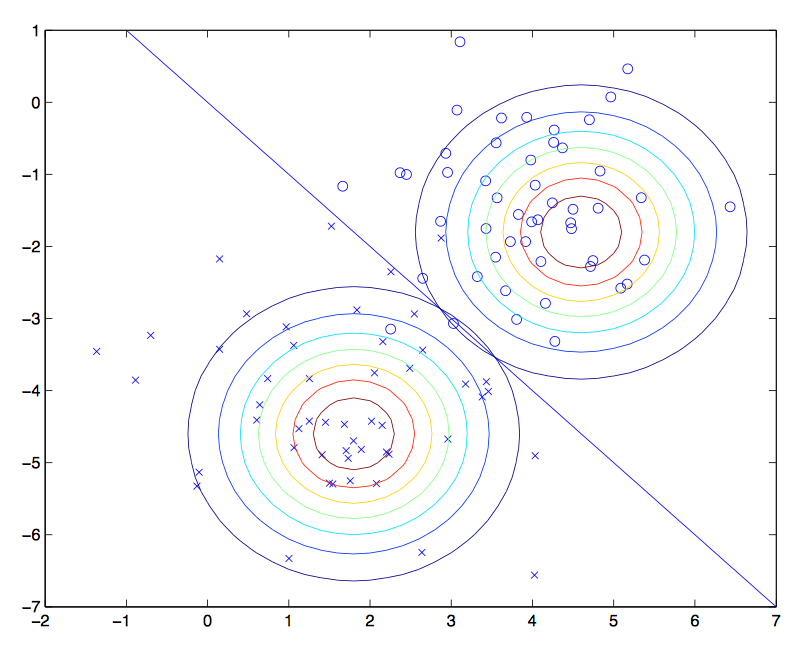
看图说话,线性回归中我们最终是得到了一条直线来分割两种不同种类的点。那么高斯判别分析就是希望能拿两个高斯分布去拟合这两和不同种类的点。点离高斯分布的中心越近属于这个分类的概率也就越大。
朴素贝叶斯
高斯判别分析中特征向量x是连续值,如果x为离散值,那么我们可以考虑使用朴素贝叶斯分类。
问题背景
邮件服务应该是我们很常用的一个服务了,一般的邮件服务里面都会有垃圾邮件自动归类的服务提供。那么给你一份邮件你如何判断这封邮件是否是垃圾邮件(y=1)呢。
我们之前的所有模型特征向量的值都是连续的,但这里如果我们以邮件的每个单词作为特征的话,那这样的特征是离散的,我们如何表示这样的离散特征呢。
一般使用的是词向量法,即找到一个字典我们假设我们的字典长度为50000,向量中的每个维对应了字典中的一个词:
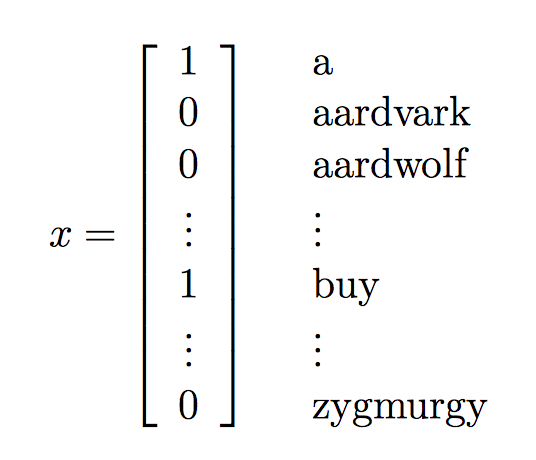
样本集描述:
\[(x,y)\in D, x\in \{0,1\}^{50000}, y\in \{0,1\}\]
构造假设
我们要求的是p(y|x),通过生成式模型我们知道了p(y|x)可以表示成P(x|y)和p(y)。于是我们先对p(x|y)进行建模。但是如果我们对x直接进行多项式分布建模。那么我们参数就会有\(2^{50000}\)个,因为50000个词的话就会有\(2^{500000}\)结果。如果不明白的查一下多项式分布。
所以我们要做一个假设:x中的特征是条件独立的。这个假设就叫做朴素贝叶斯假设。也就是说,如果出现澳门和赌场两个词,我们就假设这两个词的出现是独立的。但实际上澳门和赌场这两个词一起出现的概率会大于单独出现的概率。
这样我们的p(x|y)就转化为:
\[ \begin{array} { l } { p ( x _ { 1} ,\dots ,x _ { 50000} | y )= p ( x _ { 1} | y ) p ( x _ { 2} | y ,x _ { 1} ) p ( x _ { 3} | y ,x _ { 1} ,x _ { 2} ) \cdots p ( x _ { 50000} | y ,x _ { 1} ,\ldots ,x _ { 49999} ) } \\ { = p ( x _ { 1} | y ) p ( x _ { 2} | y ) p ( x _ { 3} | y ) \cdots p ( x _ { 50000} | y ) } \\ { = \prod _ { i = 1} ^ { n } p ( x _ { i } | y ) } \end{array} \]
第一个等号与第二个等号的转化用的就是朴素贝叶斯假设。
于是假设函数就为:
\[ h(x)= arg\max_y\left( \prod _ { i = 1} ^ { 50000 } p \left( x _ { i }|y\right) \right) p ( y) \]
衡量误差
先引入几个符号:
\[ \left.\begin{array} { l } { \phi _ { i | y = 1} = p ( x _ { i } = 1| y = 1) } \\ { \phi _ { i | y = 0} = p ( x _ { i } = 0| y = 1) } \\ { \phi _ { y } = p ( y = 1) } \end{array} \right. \]
\(\phi _ { i | y = 1} = p \left( x _ { i } = 1| y = 1\right)\)表示垃圾邮件(y=1)里第\(x_i\)出现的概率。第二条式子的y反了一下是为了与第三条式子相乘。
还是最大似然估计:
\[ \mathcal { L } \left( \phi _ { y } ,\phi _ { j | y = 0} ,\phi _ { j | y = 1} \right) = \prod _ { i = 1} ^ { m } p \left( x ^ { ( i ) } ,y ^ { ( i ) } \right) \]
求解问题
\[ \phi _ { j | y = 1} = \frac { \sum _ { i = 1} ^ { m } 1\left\{ x _ { j } ^ { ( i ) } = 1\wedge y ^ { ( i ) } = 1\right\} } { \sum _ { i = 1} ^ { m } 1\left\{ y ^ { ( i ) } = 1\right\} } \]
\[ \phi _ { j | y = 0} \quad = \frac { \sum _ { i = 1} ^ { m } 1\left\{ x _ { j } ^ { ( i ) } = 1\wedge y ^ { ( i ) } = 0\right\} } { \sum _ { i = 1} ^ { m } 1\left\{ y ^ { ( i ) } = 0\right\} } \]
\[ \phi _ { y } = \frac { \sum _ { i = 1} ^ { m } 1\left\{ y ^ { ( i ) } = 1\right\} } { m } \]
那么假设函数就可以改写成:
\[ h(x)= arg\max_y \prod _ { i = 1} ^ { 50000 } \phi _ { i | y } \phi _ { y }\]
拉普拉斯平滑
这样求解出来还有一个小问题,就是对于数据非常稀疏的情况,比如序号为35000的词从来没在邮件中出现过,那么$\phi _ { 35000} | y $:
\[ \phi _ { 35000| y = 1} = \frac { \sum _ { i = 1} ^ { m } 1\left\{ x _ { 35000} ^ { ( i ) } = 1\wedge y ^ { ( i ) } = 1\right\} } { \sum _ { i = 1} ^ { m } 1\left\{ y ^ { ( i ) } = 1\right\} } = 0 \]
\[ \phi _ { 35000| y = 0} = \frac { \sum _ { i = 1} ^ { m } 1\left\{ x _ { 35000} ^ { ( i ) } = 1\wedge y ^ { ( i ) } = 0\right\} } { \sum _ { i = 1} ^ { m } 1\left\{ y ^ { ( i ) } = 0\right\} } = 0 \]
假设函数中有一个连乘操作,那么只要其中一个值为0,整个值都会为零。即
\(p ( y | x )=0\)。也就是说只要邮件中出现过之前训练中没出现过的词的话,那么会导致这个假设函数失效。
于是我们要做一下平滑处理,对于没出现过的词给予一个很小的值而不是0值。
于是将求解得到的\(\phi_j\)进行拉普拉斯平滑处理:
\[ \phi _ { j } = \frac { \sum _ { i = 1} ^ { m } 1\left\{ z ^ { ( i ) } = j \right\} + 1} { m + k } \]
分子加1,分母加k,即\(\sum _ { j = 1} ^ { k } \phi _ { j } = 1\)
小结
这部分主要讲了两个生成式算法,x是连续值用高斯辨别分析,离散值则用朴素贝叶斯分析。