质因数分解的一些讨论（Pollard-Rho算法）

一类问题：对于一个整数n，将n进行质因数分解

算法1：

根据定义直接枚举，直接给出代码：

void Decom(int n) {
    int i;
    vector<int> res;
    for(i = 2; i <= n; i++) {
        while(n%i == 0) {
            res.push_back(i);
            n /= i;
        }
    }
    for(i = 0; i < res.size()-1; i++) printf("%d*", res[i]);
    printf("%d\n", res.back());
}

算法2：

考虑到若有 $i$ 满足n % i == 0，则必有n % (n/i) == 0，所以可以仅枚举 $i$ 从2到 $\sqrt n$ ，代码如下：

void Decom(int n) {
    int i;
    vector<int> res;
    for(i = 2; i*i <= n; i++) {
        while(n%i == 0) {
            res.push_back(i);
            n /= i;
        }
    }
    for(i = 0; i < res.size()-1; i++) printf("%d*", res[i]);
    printf("%d\n", res.back());
}

Pollard-Rho算法：

该算法需要使用的大素数判定的 $Miller$ - $Rabin$ 算法，之前已经讨论过。
Miller-Rabin算法戳这里
对于一个大整数n，我们取任意一个数 $x$ 使得 $x$ 是 $n$ 的质因数的几率很小，但如果取两个数 $x_1$ 以及 $x_2$ 使得它们的差是n的因数的几率就提高了，如果取 $x_1$ 以及 $x_2$ 使得 $gcd(abs(x_1-x_2),n)>1$ 的概率就更高了。这就是Pollard-Rho算法的主要思想。

对于满足 $gcd(abs(x_1-x_2),n)>1$ 的 $x_1$ 和 $x_2$ ， $gcd(abs(x_1-x_2),n)$ 就是n的一个因数，只需要判断它是否为素数，若为素数，则是n的质因数，否则递归此过程。

其中判断素数就使用 $Miller$ - $Rabin$ 算法。

那么我们怎样不断取得 $x_1$ 和 $x_2$ 呢？
$x_1$ 在区间 $[1,n]$ 中随机出来，而 $x_2$ 则由x[i]=(x[i-1]*x[i-1]%n+c)%n推算出来，其中 $c$ 为任意给定值，事实证明，这样就是比较优的。

代码如下：

#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;

const int MAXN = 65;
long long x[MAXN];
vector<long long> f;

long long multi(long long a, long long b, long long p) {
    long long ans = 0;
    while(b) {
        if(b&1LL) ans = (ans+a)%p;
        a = (a+a)%p;
        b >>= 1;
    }
    return ans;
}

long long qpow(long long a, long long b, long long p) {
    long long ans = 1;
    while(b) {
        if(b&1LL) ans = multi(ans, a, p);
        a = multi(a, a, p);
        b >>= 1;
    }
    return ans;
}

bool Miller_Rabin(long long n) {
    if(n == 2) return true;
    int s = 20, i, t = 0;
    long long u = n-1;
    while(!(u & 1)) {
        t++;
        u >>= 1;
    }
    while(s--) {
        long long a = rand()%(n-2)+2;
        x[0] = qpow(a, u, n);
        for(i = 1; i <= t; i++) {
            x[i] = multi(x[i-1], x[i-1], n);
            if(x[i] == 1 && x[i-1] != 1 && x[i-1] != n-1) return false;
        }
        if(x[t] != 1) return false;
    }
    return true;
}

long long gcd(long long a, long long b) {
    return b ? gcd(b, a%b) : a;
}

long long Pollard_Rho(long long n, int c) {
    long long i = 1, k = 2, x = rand()%(n-1)+1, y = x;
    while(true) {
        i++;
        x = (multi(x, x, n) + c)%n;
        long long p = gcd((y-x+n)%n, n);
        if(p != 1 && p != n) return p;
        if(y == x) return n;
        if(i == k) {
            y = x;
            k <<= 1;
        }
    }
}

void find(long long n, int c) {
    if(n == 1) return;
    if(Miller_Rabin(n)) {
        f.push_back(n);
        return;
    }
    long long p = n, k = c;
    while(p >= n) p = Pollard_Rho(p, c--);
    find(p, k);
    find(n/p, k);
}

若仍然不能理解，戳这里
以下可以略去：

关于此算法名称的来历：
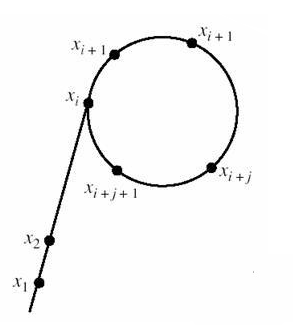
由于该算法在推算 $x[i]$ 时，最后必定会出现 $x[i+j]=x[i]$ ，然后把 $x[i]$ 按照一种神奇的方式写下来，就会长得像希腊字母 $\rho$ 。。。
如下图：
这里写图片描述

然后发明者叫做 $Pollard$ ，所以就叫做了这样一个神奇的名字。。