题目描述
Lemon因为偶然的原因,当上了警察局长。而一上任,他就碰到了个大麻烦:追捕周克华。
周克华是人尽皆知的抢劫杀人犯,而就在几天前,他在Lemon辖区内的银行门口,枪杀了一名储户后逃之夭夭。Lemon知道,如果他抓不住周克华,他的警察局长恐怕就当不下去了。为了能继续当他的警察局长,Lemon决定倾警察局之物力全力追捕。Lemon的辖区可以表示为一张边上带权的无向图。银行位于结点1。
Lemon仔细研究周克华的案底后得出以下结论:
首先,周克华拥有极强的反侦查能力,因此,他深知不走回头路的重要性。他永远不会访问任何一个结点两次。
其次,周克华深知多走一分钟路就多一分钟暴露的危险,而且他之前已经完全摸清了辖区的地形,因此他总是走最短路,也就是,他访问任何一个结点时,走的路线都是从银行到这里的最短路。为了简化题目,我们保证从银行(结点1)到任何一个结点的最短路都是唯一的。
再次,周克华知道,为了尽可能远离案发现场,他必须不停的运动。也就是说,只要有相邻的结点能满足“不走回头路、只走最短路”的前提,他一定会移动。如果有多个相邻结点可供选择,他会随机等概率选择一个作为他的移动目标。如果没有结点满足这一要求,那么周克华就会选择遁入深山之中,而可以想象在距离案发现场十万八千里的山区里抓捕周克华的难度,所以一旦周克华遁入山中,也就意味着Lemon的抓捕行动失败了。
Lemon分析出了以上结论后决定,只能在结点上布置警察,实施埋伏抓捕。但是,周克华的身体素质、反侦查能力和使用武器技术都十分优秀,因此,即使周克华遇到了埋伏,也有一定几率杀害所有参与埋伏的警察后逃脱。当然,随着埋伏的警察的数目的增多,逃脱几率会减小。如果逃脱成功,周克华会像什么都没发生一样,继续按上文所述的方式行动。
注意,周克华一旦到达一个结点,埋伏在那里的警察会立即实施抓捕,只有周克华逃脱了在当前结点的抓捕后才能进行下一步行动(遁入群山或继续移动),包括结点1,也就是周克华需要先逃脱结点1的埋伏才能走出他的第一步。
Lemon知道,他的设置警力方式决定了追捕成功的概率。他现在已经知道了他的辖区地图以及在不同地点设置不同数量的警力能成功抓捕周克华的概率,Lemon现在想要找到一个尽量优的方式设置警力,因此求助于你。你能告诉Lemon在最优的设置下,抓捕成功概率是多少吗?Lemon到时或许会把高额的悬赏分给你一部分的哦。
输入输出格式
输入格式
输入文件第一行包含两个数N,M,分别表示辖区里的结点数目和边的数目。
接下来M行,每行3个数a、b、c,表示结点a和b之间有一条权值为c的无向边。
接下来一个数S,表示可以参与埋伏的警察个数。
接下来N行,每行S个数,第i行第j个数Pij表示在结点i埋伏j个警察抓捕成功的概率。注意,如果不埋伏任何警察,那么显然绝不可能成功抓住周克华。
输出格式
输出文件仅包含一个实数,保留到4位小数,表示在最优警力设置下,抓捕成功的概率。
样例
INPUT
4 4
1 2 1
1 3 2
2 4 3
3 4 1
2
0.01 0.1
0.5 0.8
0.5 0.8
0.7 0.9
OUTPUT
0.6000
HINT
地图如下。(括号内的数为权值)
1 ---(1)--- 2
| |
| |
(2) (3)
| |
| |
3 ---(1)--- 4周克华在结点1会等概率选择2或3逃跑。如果选择了2,那么下一步他会选择遁入群山,因为1已经访问过了,而继续往4走就不是最短路了(1=>3=>4比1=>2=>4短);
如果选择了3,那么下一步他会继续往4跑,然后选择遁入群山(到达4后继续往2跑也不是最短路)。
最优警力设置是:在2、4处各设置一名警察。这样如果周克华在第一步选择了2(50%概率),那么在2处有50%概率被抓,如没有被成功抓住则遁入群山。如果第一步选择了3(50%概率),在3处被抓概率为0(因为没有警察埋伏),但接下来周克华会往4走(100%概率),在4处被抓的概率是70%所以总成功率是50%50%+50%70%=0.6。
数据范围 Data Range:
对于20%数据,满足N、S≤6;
对于50%数据,满足N、S≤30,每个结点度数不超过3;
对于100%数据,满足N、S≤200,M≤20000,1≤a、b≤N,1≤c≤10000,0<Pij≤1。
数据保证图中没有自环或重边,从结点1到任何一个结点的最短路唯一。
SOLUTION
最短路树+树形dp(树上背包)
其实这题看了题面就可以get它是让我们先求个以\(1\)为源点的单源最短路在跑个dp,然后又已知题目保证最短路的唯一性,且犯人并不会走回头路,我们就可以想到满足题意的路径构成为一棵最短路树。(考场上没想到“最短路树”这个词,想到的解法却是求最短路树的qwq)。
因为数据范围十分友好,是可以\(O(n^3)\)乱做爆搞的类型,所以果断选择Floyd做了非常简单的最短路处理。
最短路树的构建也十分简单,跟最短路图的构建差不多,在计算出点\(u,v\)以\(1\)为起点的最短路长度\(dist[u],dist[v]\)之后,对于\(u,v\)之间边权为\(w\)的边\(u→v\),若\(dist[v]==dist[u]+w\)则可以判定边\(u→v\)在最短路树上,否则边\(u→v\)一定不在最短路上。
构建完最短路树,就开始考虑dp,显然地dp数组是要开两维的,\(dp[i][j]\)代表第\(i\)个节点布置\(j\)个警察的情况,然后因为是要把\(S\)个警察分配到不同节点(也可能只有一个),自然而然地想到了背包。
考场上我想到了做背包,因为懒得在dfs里滚背包,所以就在跑完一遍最短路树之后顺便通过取这个点的父节点的分叉数的倒数\(cntp\)乘以父节点被经过的概率,把从源点到每个点的概率算出来,最后直接在原有的概率\(p[i][j]\)基础上乘以我们所算的概率,再在dfs外面滚背包。然后就爆掉了,考场上我还把背包的循环套错了导致直接爆零,考后按照这个思路改掉循环也只能有30pts。
我的算概率的思路在我看来没有问题一开始旁边人也没有找到错误所在,但是,在拜托zzr帮我找错误的时候发现:如果这么算的话,我在某些测试点输出的答案可能会大于\(1\)。
为什么会出这种问题?zzr一开始没有办法表述他的感觉,然后我为了证明这种情况的可能性,我画了一个这样的图:
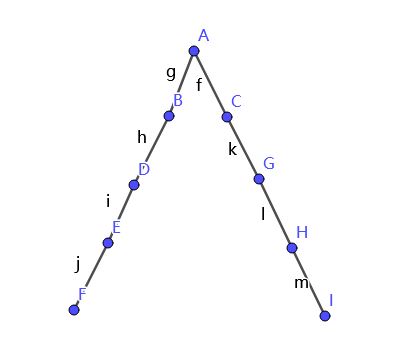
可以看出在这棵有一点丑的树上,根据我的计算,除了根节点外,每一个点被访问的概率都是\(\frac 1 2\),然后当我们的节点足够多或者是我们警察抓获犯人的概率足够大的情况下,我们的最终答案是有可能超过\(1\)的,这显然是错误的。
那么为什么是错误的呢?因为在我们这么算的时候,可能会把父节点拦截成功的概率加上了子节点拦截成功的概率,这是不符合题意的,因为犯人只有一个,在父节点拦截成功后的子节点是不可能会出现犯人的,自然没有拦截成功一说。所以我们的子节点\(v\)被访问的概率其实是\(cntp*(1.0-p(放走))\),又因为我们在父节点\(u\)布置警力的情况不同概率不同,所以不能单纯地乘上\(p[u][k]\)(\(k\)是做背包时用的位置指针)。倒不如说我们的答案构成有两种:
- 父节点\(u\)不放警察。我们在\(u\)把犯人放跑的概率为\(1\)。
- 父节点\(u\)放了\(k\)名警察。我们在\(u\)把犯人放跑的概率为\((1-p[u][k])\),所以这样可以得到:我们的所有子节点被访问的概率此时应该都是\((1-p[u][k])*cntp\)。至于子节点以及子节点的子节点的警力的分配,直接背包做就行了,与前面的概率无关。最后乘上那个概率就行了。
所以我们就可以知道,只有在父节点\(u\)布置警力的情况下,我们才要把子节点的答案在转移时乘上访问概率。所以我们可以先按情况1做一遍背包,再在父节点\(u\)布置警力个数\(k\)确定(枚举)的情况下,计算情况2能否更新。
情况1的转移就是很普通的背包(当然要乘上基本的\(cntp\),因为不管是哪个情况都要乘)
情况2的转移方程就是\(dp[u][j+k]=Max(dp[u][j+k],dp[v][j]*(1-p[u][k])+p[u][k])\)。
最后提醒一句:因为显然地,同一个节点不能多次参与答案的构成,所以做背包的时候要另开一个数组\(rec\)防止以上情况的发生(相当于\(rec\)记录了\(dp\)在被节点\(i\)更新前的答案)。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
using namespace std;
#define Min(a,b) ((a<b)?a:b)
#define Max(a,b) ((a>b)?a:b)
inline int read(){
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9') {if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9') {x=x*10+ch-48;ch=getchar();}
return x*f;}
const int N=210;
const int INF=200001000;
int n,m,S,sq[N][N],dist[N][N];
double dp[N][N],p[N][N],w[N],rec[N];
void dfs(int u){
int cnt=0,q[N];
for (int i=1;i<=n;++i){
if (!sq[u][i]) continue;
if ((dist[1][u]+sq[u][i])==dist[1][i]) {q[++cnt]=i;dfs(i);}
}
if (!cnt) {for (int i=1;i<=S;++i) {dp[u][i]=p[u][i];}return;}
double cntp=(double)1/cnt;
for (int i=1;i<=cnt;++i){
int v=q[i];
//printf("%d:%d\n",u,v);
for (int j=0;j<=S;++j) rec[j]=dp[u][j];
for (int j=S;j>=1;--j){
for (int k=(S-j);k>=0;--k){
if (rec[k]>=0) dp[u][j+k]=Max(dp[u][j+k],
rec[k]+cntp*dp[v][j]);
}
}
}
for (int j=0;j<=S;++j) rec[j]=dp[u][j];
for (int j=1;j<=S;++j){
for (int k=(S-j);k>=0;--k){
if (rec[k]>=0) dp[u][j+k]=Max(dp[u][j+k],(1.0-p[u][j])*rec[k]+p[u][j]);
}
}
}
int main(){
//freopen("catch.in","r",stdin);
//freopen("catch.out","w",stdout);
int i,j;
memset(sq,0,sizeof(sq));
n=read();m=read();
for (i=1;i<=n;++i) for (j=1;j<=n;++j) dist[i][j]=INF;
for (i=1;i<=m;++i){int u=read(),v=read(),w=read();
sq[u][v]=w;sq[v][u]=w;dist[u][v]=w;dist[v][u]=w;}
S=read();
for (i=1;i<=n;++i) {for (j=1;j<=S;++j) dp[i][j]=-1;dp[i][0]=0;}
for (i=1;i<=n;++i) for (j=1;j<=S;++j) scanf("%lf",&p[i][j]);
for (i=1;i<=n;++i) {p[i][0]=0;dist[i][i]=0;}
for (int k=1;k<=n;++k)
for (i=1;i<=n;++i)
for (j=1;j<=n;++j){
if ((dist[i][k]!=INF)&&(dist[k][j]!=INF))
dist[i][j]=Min(dist[i][j],dist[i][k]+dist[k][j]);
}
dfs(1);
double ans=0;
//for (i=1;i<=S;++i) ans=Max(ans,dp[i]);
//for (i=1;i<=n;++i) {for (j=0;j<=S;++j) printf("*%0.4lf ",dp[i][j]);puts("");}
for (i=1;i<=S;++i) ans=Max(ans,dp[1][S]);printf("%0.4lf",ans);
return 0;
}