上篇讲到了对偶的式子即:
但是什么是对偶?从哪里能体现到对偶的特性?上面的式子为什么是对求最大值?之前不是求最小问题吗?下面给大家讲解一下原因。
先给出最初的求最小值的表达式,存在约束条件:
受限于
为了容易数学计算,通过拉格朗日乘子法把约束项添加到求极值的式子中即:
其中要求
现在我们来分析一下,这个式子所代表的物理意义:
首先对求极大值即:
好,到这里我们先看看为什么是对
求极大值而不是极小值呢?(此时针对的是未知数
,w和b可以先默认为常数即梯度中提的控制变量)
主要原因是我们引入了约束条件,先分析一种情况即满足约束的情况:
如果,则
,又因为
,所以整个约束项
的,如果此时
对
求极大值,那么
应该最小才对,因
,被减数不变的情况下,减数越小,值就越大,所以此时
取0,即我们的式子为:
和最初的式子一样了,也就是说在满足条件的情况下,并不影响我们最初所求的式子,如果不满足约束条件呢?
如果时,同理可得:
,此时
对
的极大值为
即无穷大,此时的
为无穷大,这个时候我们最初的式子就被淹没了,即使w,b你取任意值都无法求得极小值,这就是加入约束项所导致的结果,这时候大家会不会想,是不是一旦类别分错了是不是就意味着无法求解,目前是这样的,但是后面会针对分错引入松弛变量或者是惩罚函数可以很好的解决这个分错就会无穷大的问题,后面会详细讲解。
好 到这里 我们再看看这个式子:
现在大家应该不难理解了,上式先针对求L的极大值,如果满足约束条件,则再去针对w,b的极小值这样就可以解决问题了,但是呢?这样求解并没有那么简单,怎么办呢?此时就引入了对偶的特性即:
大家能看到这个式子和上面的式子有什么不同呢?是的,求极值的顺序不同了,这里是先对w,b进行求极小值,然后在对求极大值,这就是对偶了即max和min对调,具有对偶特性(对偶是用字数相等、结构形式相同、意义对称) ,大家知道对偶的原因了吧,现在我们再看看这样做是否合理呢?
我们先从直观上来看一下,对偶之前所求的是最大值中的最小值,对偶之后所求的最小值中的最大值,从表面看最大值中的最小值也要比最小值中的最大值要大,可以说,对偶后的值是对偶前的值的一个下届,其实在某些条件下他们是等价的,数学中有证明,对偶的目的是什么呢?其实就是为了消去w、b,现在就可以对w、b求偏导,令其等于0,然后在带入上式就得到下面这个式子了:
这里就解释了为什么求最大值的原因的了,这个式子有什么特点呢?
我们先看看这样化简有什么好处?
第一个好处就是未知数的个数下降了, 把前面含有w和b的未知数消去了,现在的未知数只剩下和
,其他未知数都为已知量,只需要求出
就可以求出w和b了:
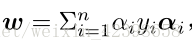
所以现在把问题转移到求拉格朗日因子上了,现在的问题是怎么求 ,
这个形式一般是通过MSO算法(Sequential minimal optimization),什么是SMO算法呢?在讲解之前还要先讲一下线性不可分情况(这里狭隘理解为线性不可分,因为这里的不可分属于离群值的处理),我们从开始到现在都是线性可分的分情况即:
数据没有相互重合交叉的,然而这是理想情况的数据,现实中更多的数据是线性不可分的,是如下情况:
这样的数据无法使用线性函数进行分离,如果使用上面的推到过程会面临一个问题,前面提到过,在引入拉格朗日乘子时,如果是不满足约束条件,结果就会是无穷大,无法分类,然而我们常见的数据就是这样的,怎么办才能使用支持向量进行处理呢?
解决方法为引入松弛变量和惩罚函数:
上图红线和蓝线就是边界线了,而绿线就是分离平面了(针对高维来说),我们最初的目标是希望边界空间越大越好,求倒数后就是越小越好,这是针对线性可分的情况,现在的问题是我们的数据并不是都在一侧或者你找不到一个线性可分的分离面,如上图中的紫线,在实点的分类中有两个空心点,而空心点中有一个实心点,基于此我们引入惩罚函数,如下式,其中
是数据点距离正确分类那边边界线的距离即是紫线所示,约束项1-
的意思就是针对错误数据进行偏移边界线,相当于平移边界线,怎么体现我们希望边界空间越大越好,分错的点越少越好的特性呢?在原理的基础上增加惩罚项,同时增加一个松弛因子,使其总和最小的意思就是希望边界空间尽量的大,同时希望分错的点尽量的小。
公式中蓝色的部分为在线性可分问题的基础上加上的惩罚函数部分,当xi在正确一边的时候,ε=0,R为全部的点的数目,C是一个由用户去指定的系数,表示对分错的点加入多少的惩罚,当C很大的时候,分错的点就会更少,但是过拟合的情况可能会比较严重,当C徆小的时候,分错的点可能会徆多,不过可能由此得到的模型也会不太正确,所以如何选择C是有徆多学问的,不过在大部分情况下就是通过经验尝试得到的。
现在我们来详细看看为什么是1-,松弛因子到底如何降低这种离群值分错的,先给出图:
上图画圆圈的数据就是支持向量了,开始分析,我们引入的松弛变量是针对每一个数据点的,对于位于正确边缘内部和边缘边界的点
,如上图的右下角的点此时ε=0,并不影响分类,然而对于其他点
,其中
是决策边界即值为1或者-1,而
是决策面了,强调一下,上图的红线为决策平面,两边是决策边界,对于位于决策面的点
,此时
,看上图,如
说明被分错了的点,此时
,这时整个决策平面就变为
,相当于
即红线向上左上方平移了,正好可以把离群值分类正确,同理其他可能也是这样分析的,很聪明的方法,他不是一个参数针对所有点,他是通过每一个数据点进行实时调整,同时也因为增加的松弛变量,整个支持向量变多了,这在后面引入核函数后去预测新数据的计算能看出来,因为参与计算的只是支持向量参与运算,这也是起名为支持向量的关键之处。
好,到这里我们加入了线性不可分的情况,然后在进行上面的那些分析,即加入拉格朗日乘子,在经过对偶变化得到了一个新的对偶后的式子,如下(数学公式不推了,和上面一样的):
我们发现和线性可分的情况相比,只有约束条件变化,其他和线性可分形式是一样的,,而且关键的变化的是拉格朗日乘子系数有了上界,我们从上面知道,一旦线性可分分错了,结果就为无穷大,无穷大的原因就是可以取到无穷大,有了这个条件后就避免了上面的问题,其实想想也是可以想通的,因为分错的原因也是线性不可分的一种情况,因此上面的式子更具有普遍性,更适合我们真实世界的数据。
好,分析到这里我们发现无论是线性可分和不可分问题,我们把问题都转化为其拉格朗日的因子上,因此只需求出这个参数,问题就解决了,同时该式还有更好的特点,那就是可以处理高维问题,这个到后面再说,下面就是如何求解这个
参数,上面我们知道可以利用SMO算法进行求解,那么什么是SMO呢?他有什么神奇的能力可解决这个问题?
到这里基本上支持向量机的原理就讲完了,后面就是计算上面的式子了,同时计算推广到高维的情况,通常使用SMO算法进行处理,高维情况使用核函数比较方便,后面会一一详细讲解,我们下节先对smo算法进行详解。










