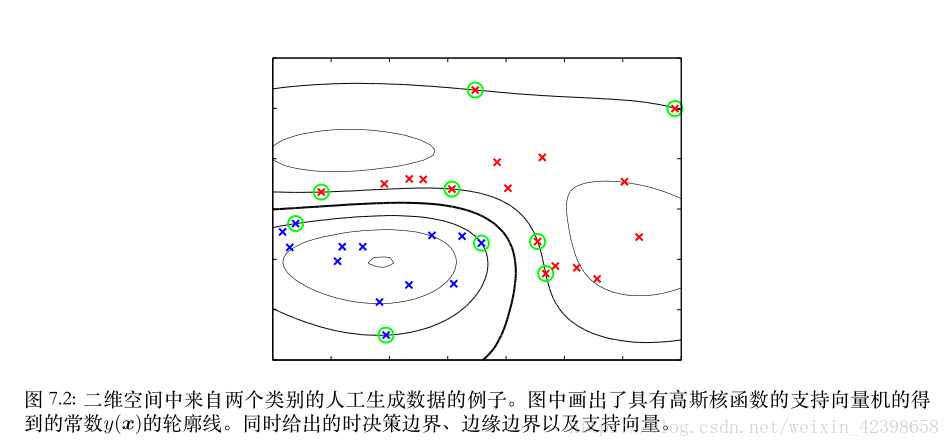
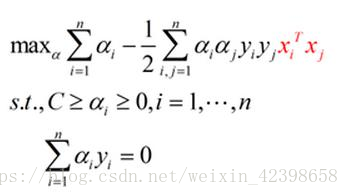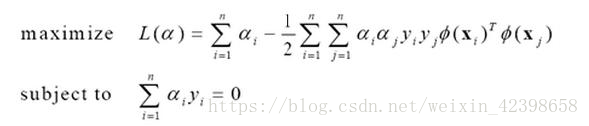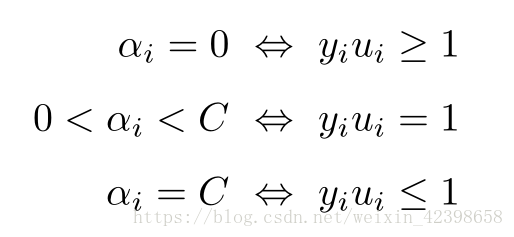前面我们曾经引入二维数据的非线性的情况,但是那种非线性(并不是真正意义上的非线性)是通过松弛因子进行优化的,如果数据比之前还复杂怎么办呢?
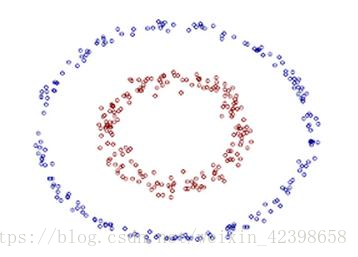
复杂到即使你怎么调节C你都无法进行分类,这个时候怎么办?如下例子:
这个无论你怎么调节参数都无法在二维平面内进行线性分离了,但是我们也可以观察到,分离的办法就是在两个数据中间画一个圆就可分了,但是这非线性了,我们就想通过线性分离怎么办呢?这个时候可以通过映射到高维空间即可,下面详解如何映射,我觉的这里的理解很重要,直接影响后面的核函数的理解,所以大家务必好好理解这个简单的例子,好废话不多说开始继续,怎么把这个线性不可分变为线性可分,然后在通过前面计算线性可分的方法进而求出分离超平面:
上图的数据在二维平面中就是两个圆,使用线性分离不可能实现,那么我们可以映射,什么映射呢?即我们把二维数据映射到更高维度中,我们的数据是二维的,但是我们可以映射到三维去看看数据,
如左图为二维的数据,黑色圆圈为一种数据,红色为另外一种数据,很明显红色的半径要大于黑色的半径,且此时在二维无法线性可分,那么我们就想到映射到更高维度进行分离,因此我们把二维数据映射到三维,映射规则是,所谓三维其实很简单就是在二维的基础上增加一维,这一维的怎么添加就是映射规则,在这里我们的映射规则为
,即第三维其实就是z轴,且这一维的值就是
即圆的半径r,那么就可以画出三维的数据图形了,简单来看,就是把二维数据沿着z轴进行平移,平移的大小和映射有关,这里我们映射规则是圆的半径,因为两圆的的半径不同,因此z值不同,也就是表现的高度不同,如上右图,我们可以清楚的看到,红色代表的数据要比黑色代表的数据高,同时二者在三维也就分离开了,此时使用一个平面就可以分离这两种数据,如上图铅笔画的分离平面,因此在这里,我们就可以使用前面的解决思路求出这个平面即可,同时我们可以以此类推,如果数据更复杂,维度更高,那么我们就可以映射到更高的维度,直到,他们可以通过线性分离实现,此时的线性就是超平面了,这个超平面就可以通过支持向量进行确定,即又回到前面的求线性分离超平面问题了,通过引入拉格朗日因子,松弛因子、在转换为对偶问题,最后通过smo算法即可求出超平面,当然这些是在知道如何映射的问题之上,所以,如果我们遇到了线性不可分问题就可以令其映射到更高维度就可以解决了。如下在二维的数据最后对偶问题是这样的:
现在呢把数据映射到更高维度,而这个映射函数使用,代入上式得到:
到这里我们呢基本上就可以解决各种非线性问题了,无论数据多复杂都没问题,因为可以通过n维映射进行分离,理论上是可以解决各种复杂的非线性问题,这就是支持向量机的牛叉之处,但是呢,这一切实现的前提是找到合适的映射函数,同时还有一个问题不可忽视那就是计算量,在这里先说一下计算量问题:
首先呢,我们知道在映射之前呢数据只需求內积就好即,假如是n维数据,那么时间复杂度为O(n),如果映射到
维,內积就变为
那么时间复杂度就是
维,计算量陡然增加,随着映射维度越高,那么计算量会陡然增加,这就是维度灾难了,同时呢?映射函数怎么找呢?如何找?
所以支持向量虽然从理论上可以解决任意的非线性分类问题,但是代价却是很大的,一是计算量、二是映射函数如何寻找问题
在很长时间里人们都在想办法解决这两个问题,终于找到了一个方法,那就是核函数,他的主要解决思路是本来我需要找到映射函数,把数据映射到高维在通过求解超平面进行分离,在求解超平面时会遇到维度灾难问题,但是呢我不需要这样做了,我能找到一种核函数把这个过程(把数据映射到高维在通过求解超平面进行分离)的计算结果直接通过核函数来代替,即数据映射到高维计算的结果,我可以通过低维的核函数进行计算出这个结果,这样就避免去找这个映射函数同时避免了维度灾难,这就是核函数的牛叉之处,也因此核函数的出现,支持向量机才得到广泛的使用,这里只是感性让大家认识一下核函数,下面通过数学方式进行详解什么是核函数。
核函数形式化定义,如果原始特征内积是,映射后为
,那么定义核函数(Kernel)为
从这个定义的式子我们可以看出,按照正常的处理方式是通过找到映射函数,然后在高维进行內积,现在呢,我可以通过核函数直接计算出这个结果,下面举个例子进行说明:
假设x和z都是n维的
![clip_image028[4]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103182034334920.png)
展开后
![clip_image030[4]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103182034348235.png)
这时候我们发现核函数计算內积的平方,时间复杂度还是O(n)而不是,因此核函数可以降低计算量
好到这里我们就解决了计算量和映射问题,那么我们我们如何去分类一个新来的数据呢?我们知道在线性可分的问题中,我们通过smo算法进行求解w、b,然后把通过 进行分类,然而我们映射后需要通过
进行求解吗?
理论上说应该这样,但是我们通过核函数计算就没有去找映射函数呀,这怎么办呢?其实根本用不到映射函数,如下图:
![clip_image055[4]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103182034444670.png)
其中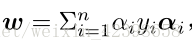
现在我们在细看这个式子其中:
我们发现最后我们预测数据x时只需和每一个训练数据进行內积 就可以了,然而高维进行內积计算量大且不易找到映射函数,因此通过核函数解决,根据前面我们引入拉格朗日乘子可知,只要训练数据点
分类正确,此时
=0,大家可以看到一旦
=0,此时的在预测中就不会参与运算,只有在分界线上的数据点才会参与运算,也就是说在预测的时候真正参与运算的只是那些支持向量,以及那些通过松弛变量引入的数据点,因此计算量会很少,下面给出图示:
此图是没有加入松弛条件的支持向量,圆圈你的就是支持向量,预测的时候也就是新数据和这些支持向量进行內积就可以了。
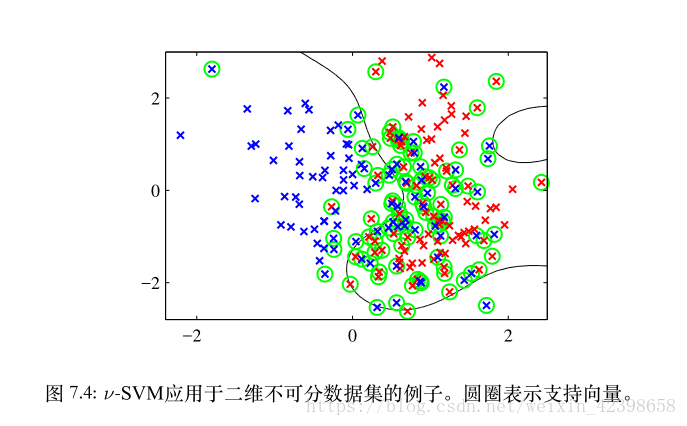
下图是加入松弛变量,我们发现加入松弛变量的支持向量变多了,说明了松弛变量的的有效性
好,到这里我们已经讲解了如何寻找映射函数和解决维度灾难问题,现在的问题是到底什么是核函数?为什么核函数具有这样的特性?这个核函数又是怎么确定的?是不是核函数是不是任意的还是有所约束呢?
核函数算式一种近似,和数学中的泰勒级数以及傅里叶变换性质差不多,就是一种近似,然后这种近似并不是无条件的的,他需要满足一定的条件,这个条件是Mercer定理,下面开始从核函数的有效性进行讲解。
核函数有效性判定:
问题:给定一个函数K,我们能否使用K来替代计算 ,也就说,是否能够找出一个
,使得对于所有的x和z,都有
![clip_image028[4]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103182034334920.png) ?
?
比如给出了![clip_image028[4]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103182034334920.png) ,是否能够认为K是一个有效的核函数。
,是否能够认为K是一个有效的核函数。
下面来解决这个问题,给定m个训练样本![]() ,每一个
,每一个![]() 对应一个特征向量。那么,我们可以将任意两个
对应一个特征向量。那么,我们可以将任意两个![]() 和
和![]() 带入K中,计算得到
带入K中,计算得到![]() 。I可以从1到m,j可以从1到m,这样可以计算出m*m的核函数矩阵(Kernel Matrix)。为了方便,我们将核函数矩阵和
。I可以从1到m,j可以从1到m,这样可以计算出m*m的核函数矩阵(Kernel Matrix)。为了方便,我们将核函数矩阵和![]() 都使用K来表示。
都使用K来表示。
如果假设K是有效地核函数,那么根据核函数定义
可见,矩阵K应该是个对称阵。让我们得出一个更强的结论,首先使用符号![]() 来表示映射函数
来表示映射函数![]() 的第k维属性值。那么对于任意向量z,得
的第k维属性值。那么对于任意向量z,得
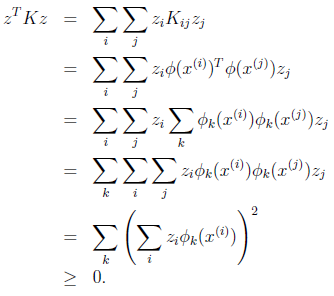
最后一步和前面计算![]() 时类似。从这个公式我们可以看出,如果K是个有效的核函数(即
时类似。从这个公式我们可以看出,如果K是个有效的核函数(即![]() 和
和![]() 等价),那么,在训练集上得到的核函数矩阵K应该是半正定的(
等价),那么,在训练集上得到的核函数矩阵K应该是半正定的(![]() )
)
这样我们得到一个核函数的必要条件:
K是有效的核函数 ==> 核函数矩阵K是对称半正定的。
可幸的是,这个条件也是充分的,由Mercer定理来表达。
Mercer定理:
如果函数K是![]() 上的映射(也就是从两个n维向量映射到实数域)。那么如果K是一个有效核函数(也称为Mercer核函数),那么当且仅当对于训练样例
上的映射(也就是从两个n维向量映射到实数域)。那么如果K是一个有效核函数(也称为Mercer核函数),那么当且仅当对于训练样例![]() ,其相应的核函数矩阵是对称半正定的。
,其相应的核函数矩阵是对称半正定的。
Mercer定理表明为了证明K是有效的核函数,那么我们不用去寻找![]() ,而只需要在训练集上求出各个
,而只需要在训练集上求出各个![]() ,然后判断矩阵K是否是半正定(使用左上角主子式大于等于零等方法)即可。
,然后判断矩阵K是否是半正定(使用左上角主子式大于等于零等方法)即可。
核函数不仅仅用在SVM上,但凡在一个模型后算法中出现了,我们都可以常使用
去替换,这可能能够很好地改善我们的算法。
到这里基本核函数就讲解完了,下一节将讲解几个重要的核函数,即
注:本篇的 核函数有效性判定来源这篇博客,本人感觉这里作者写的很详细了,就没再自己编写,在这里特此说明。