计算机视觉（二）：直方图均衡

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/eeeee123456/article/details/82911410

一、灰度空间的直方图均衡

1.直方图

      灰度级范围为[0,L-1]的数字图像的直方图是离散函数 $h(r_k)=n_k$，其中 $r_k$是第 $k$级灰度值， $n_k$是图像中灰度为 $r_k$的像素个数。在实践中，经常用乘积 $MN$表示的图像总像素除每个分量来归一化直方图，通常 $M$和 $N$是图像的行数和列数。因此，归一化后的直方图由
$p(r_k)={n_k\over{MN}}$给出，其中 $k=0,1,...,L-1$。归一化直方图的所有分量之和应等于1。
      直观上，可以得出这样的结论：若一幅图像的像素倾向于占据整个可能的灰度级并且分布均匀，则该图像会有高对比度的外观并展示灰色调的较大变换。最终效果将是一幅灰度细节丰富且动态范围较大的图像。为实现该效果，我们需要一个变换函数，将输入图像直方图信息进行变换，得到均匀分布的图像。

2.变换函数应满足条件

      考虑连续灰度值，并用变量 $r$表示待处理图像的灰度。通常，我们假设 $r$的取值区间为[0,L-1]，且 $r = 0$表示黑色， $r = L-1$表示白色。在 $r$满足这些条件的情况下，我们将注意力集中到变换函数
$s = T(r)\ \ \ \ \ \ \ \ \ \ 0≤r≤L-1$上，对于输入图像中每个具有 $r$值的像素产生一个输出灰度值 $s$。为了实现变换后的灰度值均匀分布的效果，变换函数需满足以下条件：
(a) $T(r)$在区间[0,L-1]上为单调递增函数
(b) 当 $0≤r≤L-1$时， $0≤T(r)≤L-1$，且 $T(r)$均匀分布
为了能用反函数
$r = T^{-1}(s)\ \ \ \ \ \ \ \ \ \ 0≤s≤L-1$计算原色图像，在这种情况下，条件(a)改为
(a`) $T(r)$在区间[0,L-1]上为严格单调递增函数

证明：
(a) 要求 $T(r)$单调递增，可保持原来输入值大小关系不变，即无论如何映射，较亮区域依然亮，较暗区域依然暗。
(b) 保证输出灰度值的范围与输入灰度值的范围相同，且变换后的灰度值需均匀分布。
(a`) 要求 $T(r)$严格单调递增，可保证从 $s$到 $r$的反映射是一对一的，防止出现二义性。

3.变换函数

      一幅图像的灰度级可视为区间[0,L-1]内的随机变量。随机变量的基本描述子是其概率密度函数(PDF)。令 $p_r(r)$和 $p_s(s)$分别表示随机变量 $r$和 $s$的概率密度函数，其中 $p$的下标用于指示 $p_r(r)$和 $p_s(s)$是不同的函数。
      在图像处理中，特别重要的变换函数有如下形式：
$s = T(r) = (L-1)\int_0^rp_r(w)dw\ \ \ \ \ \ \ \ \ \ (1)$式中， $w$是积分的假变量。该公式满足上述条件(a`)(b)。

证明：
公式右边是随机变量 $r$的累积分布函数(CDF)。因为PDF总为正，回忆可知一个函数的积分是该函数下方的面积，固该公式为严格递增函数，满足条件(a`)。
现证明该公式满足条件(b)：
用微积分换元法，可得：
$p_r(r)dr = p_{T(r)}(T(r)) d(T(r)) = p_s(s)ds$即
$p_s(s) = p_r(r)|{{dr}\over{ds}}|\ \ \ \ \ \ \ \ \ \ (2)$又因为
${{ds}\over{dr}} = {{dT(r)}\over{dr}} = (L-1){d\over{dr}}[\int_0^rp_r(w)dw] = (L-1)p_r(r)\ \ \ \ \ (3)$将(3)代入(2)可得
$p_s(s) = p_r(r)|{{dr}\over{ds}}| = p_r(r)|{1\over{(L-1)p_r(r)}}| = {1\over{L-1}}\ \ \ \ \ \ 0≤s≤L-1$从该式最后一行中的 $p_s(s)$可知，这是一个均匀概率密度函数。
得证。

4.直方图均衡

      对于离散值，我们处理其概率与求和来代替处理概率密度函数与积分。如前所述，一幅数字图像中灰度级 $r_k$出现的概率近似为
$p_r(r_k)={n_k\over{MN}}\ \ \ \ \ \ \ k=0,1,...,L-1$代入式(1)可得离散形式为
$s_k = T(r_k) = (L-1)\sum_{j=0}^kp_r(r_j) = {{L-1}\over{MN}}\sum_{j=0}^kn_j \ \ \ \ \ \ k=0,1,2,...,L-1\ \ \ \ \ \ (4)$通过计算上式，即可实现直方图均衡化。均衡后的图像的灰度级会跨越更宽的灰度级范围，最终结果是增强来对比度。
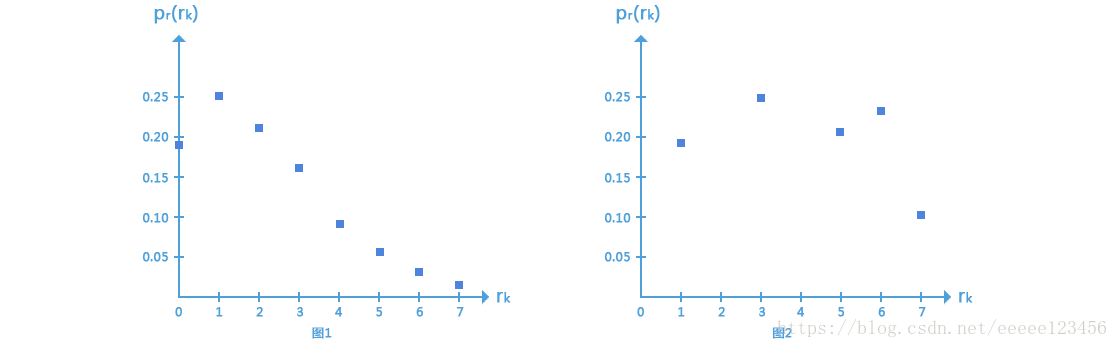
例1

$r_k$	$n_k$	$p_k(r_k) = n_k/MN$
$r_0 = 0$	790	0.19
$r_1 = 1$	1023	0.25
$r_2 = 2$	850	0.21
$r_3 = 3$	656	0.16
$r_4 = 4$	329	0.08
$r_5 = 5$	245	0.06
$r_6 = 6$	122	0.03
$r_7 = 7$	81	0.02

假设图像的直方图如图1所示，直方图均衡变换函数的值使用式(4)得到，即
$s_0 = T(r_0) =7\sum_{j=0}^0p_r(r_j) = 7p_r(r_0) = 1.33$ $s_1 = T(r_1) =7\sum_{j=0}^1p_r(r_j) = 7p_r(r_0) + 7p_r(r_1) = 3.08$及 $s_2=4.55$， $s_3=5.67$， $s_4=6.23$， $s_5=6.65$， $s_6=6.86$， $s_7=7.00$。在这一点上， $s$值一直是分数，因为它们是通过求概率值的和产生的，因此我们要把它们近似为最接近的整数：
$s_0 = 1.33 \rightarrow 1\ \ \ \ \ \ s_1 = 3.08 \rightarrow 3\ \ \ \ \ \ s_2 = 4.55 \rightarrow 5\ \ \ \ \ \ s_3 = 5.67 \rightarrow 6$ $s_4 = 6.23 \rightarrow 6\ \ \ \ \ \ s_5 = 6.65 \rightarrow 7\ \ \ \ \ \ s_6 = 6.86 \rightarrow 7\ \ \ \ \ \ s_7 = 7.00 \rightarrow 7$这是均衡后的直方图的值，如图2所示。

二、彩色空间的直方图均衡

      如果单独对RGB彩色空间的各个分量进行直方图均衡，将产生不正确的彩色。一种更合乎逻辑的方法是，均匀地展开这种彩色灰度，而保持彩色本身（即色调）不变。HSV彩色空间是适合这种方法的理想空间，即只对 $V$分量进行均衡化。

三、代码实现（Python+OpenCV)

OpenCV的equalizeHist()函数能支持对单向量直方图均衡。

1.灰度图像

import cv2

img = cv2.imread('gray.jpg',0) # 加载灰度图片
equal_img = cv2.equalizeHist(img) # 直方图均衡
cv2.imwrite('equal_gray.jpg',equal_img) # 保存图片

2.彩色图像

import cv2

img = cv2.imread('img.jpg')  # 加载BGR图片
img_hsv = cv2.cvtColor(img, cv2.COLOR_BGR2HSV) # BGR转HSV
img_v = img_hsv[:, :, 2] # 获取V分量
equal_img_v = cv2.equalizeHist(img_v) # 对V分量进行直方图均衡
img_hsv[:, :, 2] = equal_img_v # 将均衡后的V分量赋值给原图
equal_img = cv2.cvtColor(img_hsv, cv2.COLOR_HSV2BGR) # HSV转BGR
cv2.imwrite('equal_img.jpg',equal_img) # 保存图片

以上全部内容参考书籍如下：
冈萨雷斯《数字图像处理（第三版）》