计算机视觉（三）：空间域滤波基础

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/eeeee123456/article/details/82914373

一、背景知识

1.空间域

      术语空间域指图像平面本身，这类图像处理方法直接操作图像中的像素。

2.算子

      空间域处理可由下式表示：
$g(x,y) = T[f(x,y)]\ \ \ \ \ \ \ \ \ \ \ \ (1)$式中， $f(x,y)$是输入图像， $g(x,y)$是处理后的图像， $T$ 是在点 $(x,y)$的邻域上定义的关于 $f$的一种算子。算子可应用于单幅图像或图像集合。

3.变换函数

      上式(1)中的 $T$ 可写成一个灰度（也称为灰度级或映射）变换函数：
$s = T(r)$式中，为表达方便，令 $r$和 $s$分别表示变量，即 $g$和 $f$在任意点 $(x,y)$处的灰度。

二、一些基本的灰度变换函数

以下讨论图像灰度级范围为 $[0,L-1]$，其中 $L-1$归一化为1。

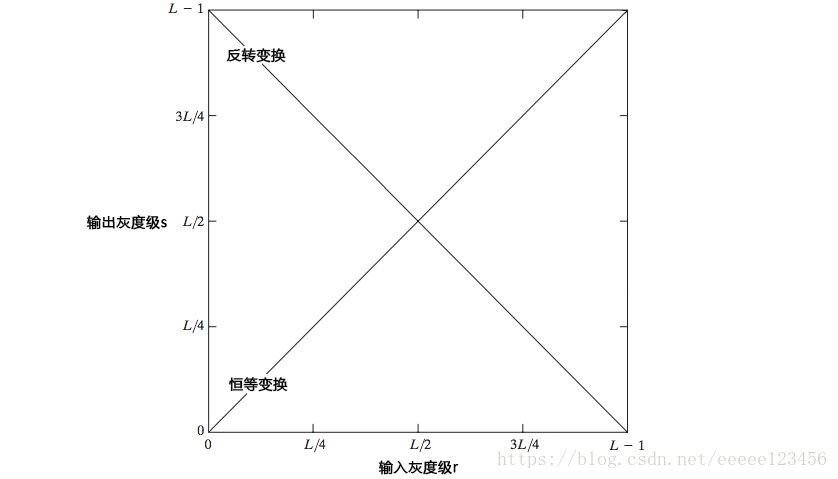
1.图像反转

      使用图1所示的反转变换，可得到灰度级范围为 $[0,L-1]$ 的一副图像的反转图像，该反转图像由下式给出：
$s = L-1-r$使用这种方式反转一副图像的灰度级，可得到等效的照片底片。

图1    图像反转

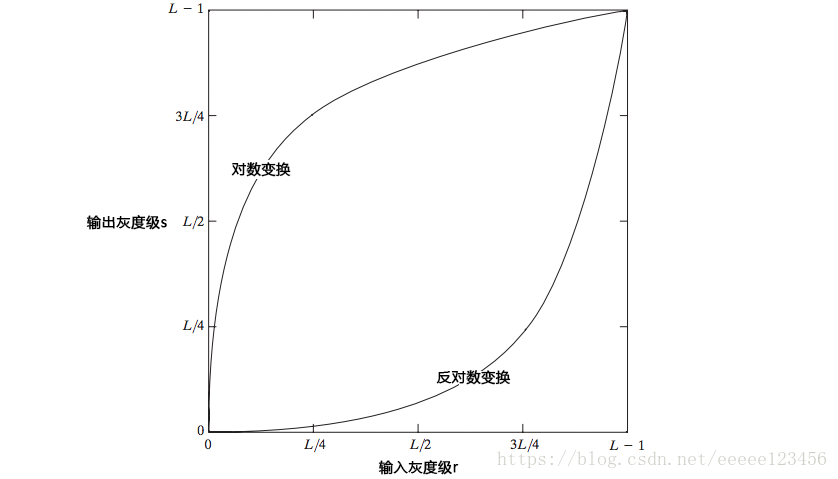
2.对数变换

对数变换的通用形式为
$s = c \log_{v+1}(1+vr)$反对数变换的形式为
$r = c \log_{v+1}(1+vs)$式中 $c$ 是常数，并假设 $r≥0$。图中对数曲线的形状表明，该变换将输入中范围较窄的低灰度值映射为输出中范围较宽的灰度值，或将输入中范围较宽的高灰度值映射为输出中范围较窄的灰度值。我们使用这种类型的变换来扩展图像中的暗像素值，同时压缩更高灰度级的值。

图2    对数变换

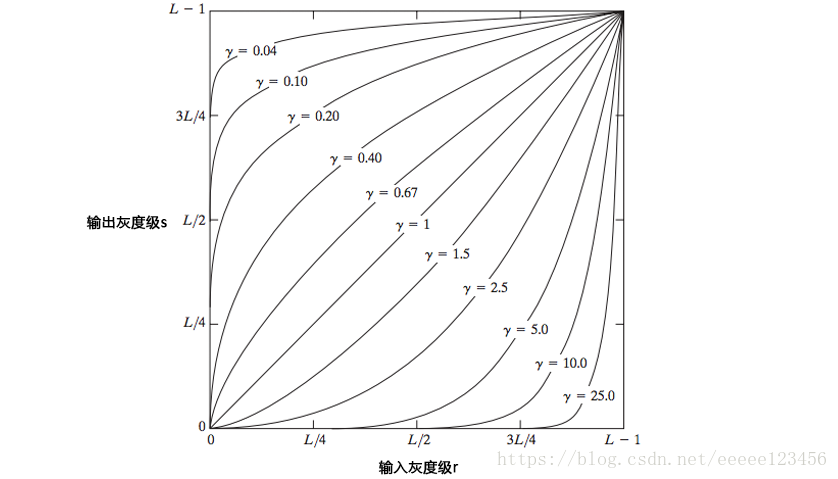
3.幂律（伽马）变换

      幂律变换的基本形式为
$s = cr^γ$式中 $c$ 和 $γ$ 为正常数。图像如图3所示。

图3    伽马变换

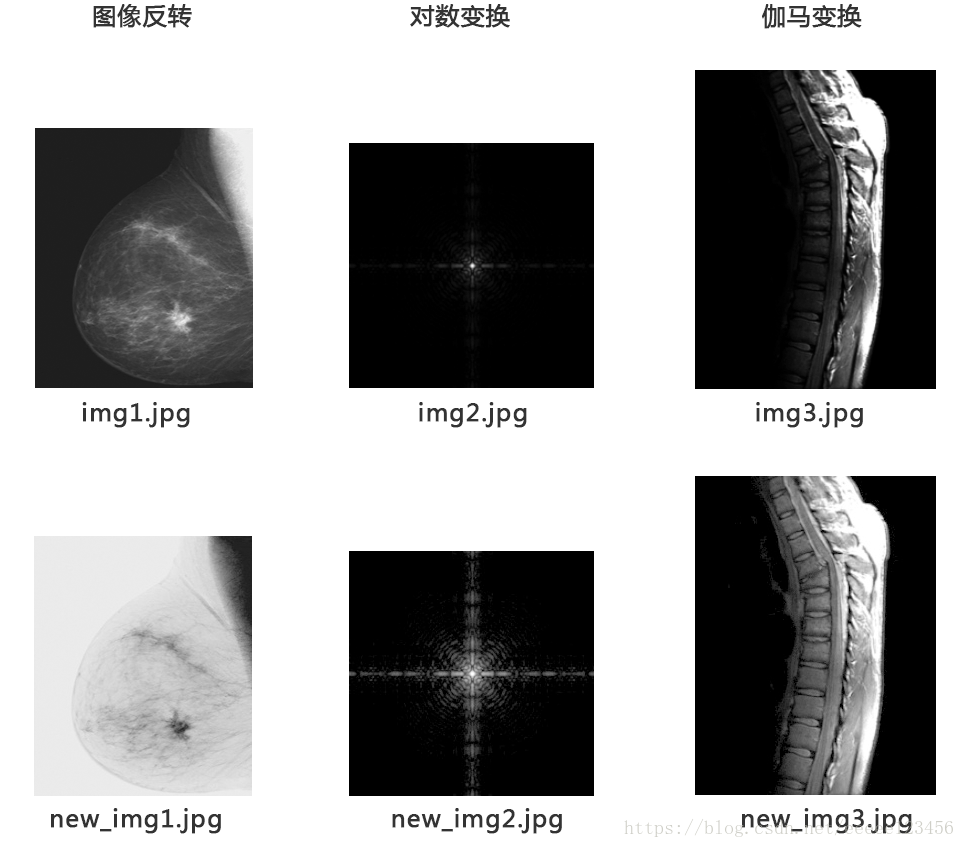
三、基本的灰度变换代码实现（Python+OpenCV)

import cv2
import numpy as np

# 图像反转
img1 = cv2.imread('img1.jpg', 0)
new_img1 = np.ones(img1.shape) * 255 - img1
cv2.imwrite('new_img1.jpg', new_img1)

# 对数变换（c = 1，v = 10）
img2 = cv2.imread('img2.jpg', 0)
img2 = img2 / 255 # 归一化为范围[0,1]
new_img2 = np.log10(1+10 * img2)
new_img2 = new_img2 * 255 # 转换为范围[0,255]
cv2.imwrite('new_img2.jpg', new_img2)

# 伽马变换（c = 1，γ = 0.6）
img3 = cv2.imread('img3.jpg', 0)
img3 = img3 / 255 # 归一化为范围[0,1]
new_img3 = np.power(img3, 0.6)
new_img3 = new_img3 * 255 # 转换为范围[0,255]
cv2.imwrite('new_img3.jpg', new_img3)

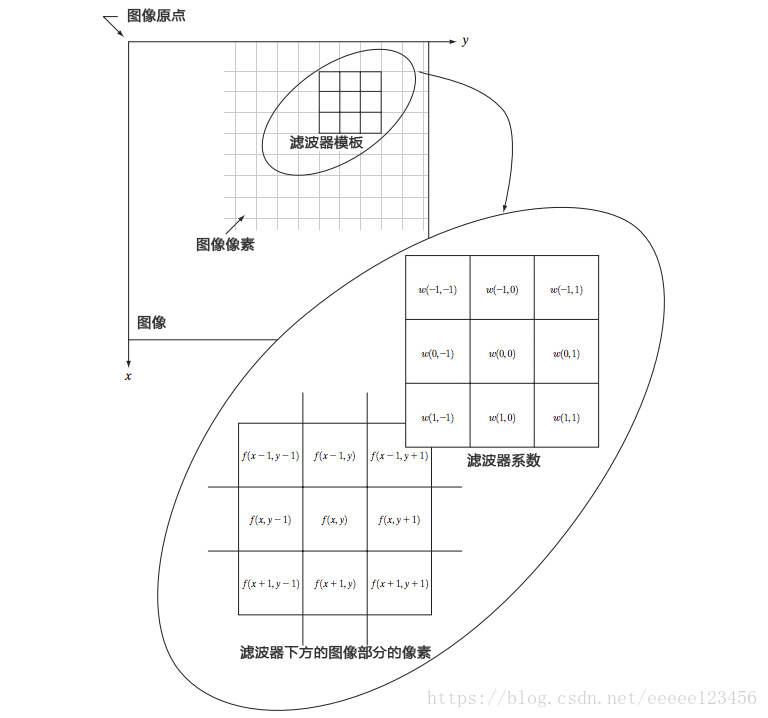
四、空间滤波机理

1.空间滤波器

      空间滤波器由一个邻域（通常是一个较小的矩形）和对该邻域所包围图像像素执行的预定义操作组成。
      滤波产生一个新像素，新像素的坐标等于邻域中心的坐标，像素的值是滤波操作的结果。滤波器的中心访问输入图像中的每个像素后，就生成了出了（滤波）后的图像。如果在图像像素上执行的是线性操作，则该滤波器称为线性空间滤波器，否则，滤波器就称为非线性空间滤波器。

2.线性空间滤波表达式

      一般来说，使用大小为 $m\times n$ 的滤波器对大小为 $M\times N$ 的图像进行线性空间滤波，可由下式表示：
$g(x,y) = \sum_{s=-a}^a\sum_{t=-b}^bw(s,t)f(x+s,y+t)$式中， $x$ 和 $y$ 是可变的，以便 $w$ 中的每个像素可访问 $f$ 中的每个像素。

图4    使用大小为3×3的滤波器模板的线性空间滤波的机理。表示滤波器模板系数的坐标所选择的形式简化了线性滤波的表达式。

五、空间相关与卷积

1.定义

      相关是滤波器模板移过图像并计算每个位置乘积之和的处理。卷积的机理相似，但滤波器首先要旋转180° 。

2.表达式

      一个大小为 $m\times n$ 的滤波器 $w(x,y)$ 与一副图像 $f(x,y)$ 做相关操作，可表示为 $w(x,y)☆f(x,y)$：
$w(x,y)☆f(x,y) = \sum_{s=-a}^a\sum_{t=-b}^bw(s,t)f(x+s,y+t)$这一等式对所有位移变量 $x$ 和 $y$ 求值，以便 $w$ 的所有元素访问 $f$ 的每个像素，其中我们假设 $f$ 已被适当地填充。
      类似地， $w(x,y)$ 和 $f(x,y)$ 的卷积表示为 $w(x,y)★f(x,y)$：
$w(x,y)★f(x,y) = \sum_{s=-a}^a\sum_{t=-b}^bw(s,t)f(x-s,y-t)$其中等式右侧的减号表示翻转 $f$（即旋转180° ）。为简化符号表示，我们遵循惯例，翻转和移位 $w$ 而非 $f$，结果是一样的。

3.一维空间例子

      图5显示了一个一维函数 $f$ 和一个滤波器 $w$ 执行相关和卷积操作的结果。我们注意到的第一件事情是存在未覆盖的部分函数，该问题的解决办法是在 $f$ 的任意一侧补上足够的 $0$。
      零填充并不是唯一的选择。例如，我们可在 $f$ 的两侧复制第一个元素和最后一个元素 $m-1$ 次，或镜像第一个元素和最后一个元素 $m-1$ 次，并为填充使用镜像后的值。

图5

4.多维空间例子

以上全部内容参考书籍如下：
冈萨雷斯《数字图像处理（第三版）》