学习深度学习看到卷积这个operation,为了理解它查了一些资料,有幸看到一个大佬的总结,再加上一些自己的想法,做一个总结。
一、卷积的定义
内涵:
在泛函分析中,卷积、旋积或摺积(英语:Convolution)是通过两个函数f 和g 生成第三个函数的一种数学算子,表征函数f 与g经过翻转和平移的重叠部分的面积。
设:f(x),g(x)是R1上的两个可积函数,作积分:
可以证明,关于几乎所有的实数x,上述积分是存在的。这样,随着x的不同取值,这个积分就定义了一个新函数h(x),称为函数f与g的卷积,记为。
定义:
卷积是两个变量在某范围内相乘后求和的结果。如果卷积的变量是序列和
,则卷积的结果
其中星号*表示卷积。当时序时,序列
是
的时序
取反的结果;时序取反使得
以纵轴为中心翻转180度,所以这种相乘后求和的计算法称为卷积和,简称卷积。另外,n是使
位移的量,不同的n对应不同的卷积结果。这句话解释了内涵中翻转和平移的重叠部分的面积。n=0时,
,函数
翻转180度,平移n(此时为0),然和乘积求和。
如果卷积的变量是函数和
,则卷积的计算变为
,
其中是积分变量,积分也是求和,
是使函数
位移的量,星号*表示卷积。
二、理解卷积
首先选取知乎上对卷积物理意义解答排名最靠前的回答。
不推荐用“反转/翻转/反褶/对称”等解释卷积(上边我们讲了使用翻转的 - -)。好好的信号为什么要翻转?导致学生难以理解卷积的物理意义。
这个其实非常简单的概念,国内的大多数教材却没有讲透。
直接看图,不信看不懂。以离散信号为例,连续信号同理。
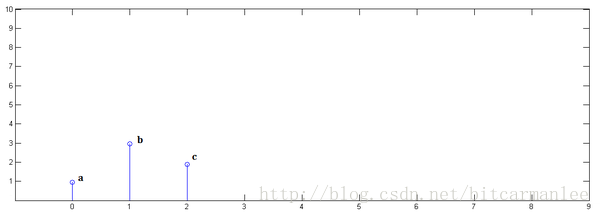
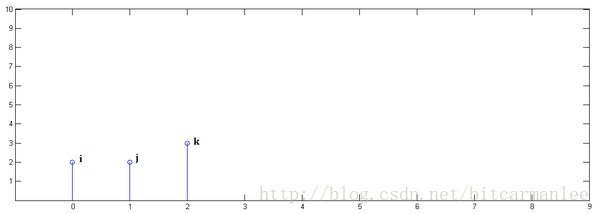
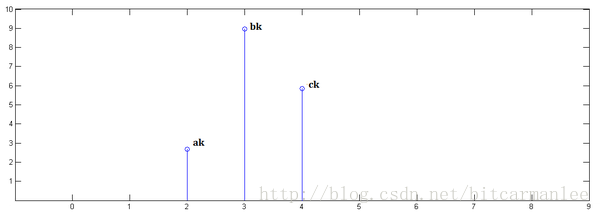
已知
已知
下面通过演示求的过程,揭示卷积的物理意义。
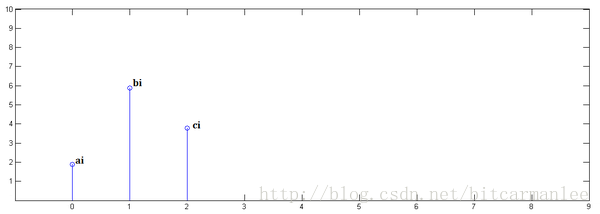
第一步,乘以
并平移到位置0:
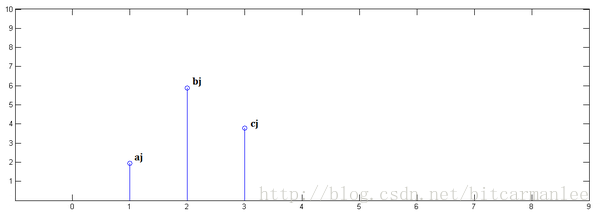
第二步,乘以
并平移到位置1 :
第三步,乘以
并平移到位置2:
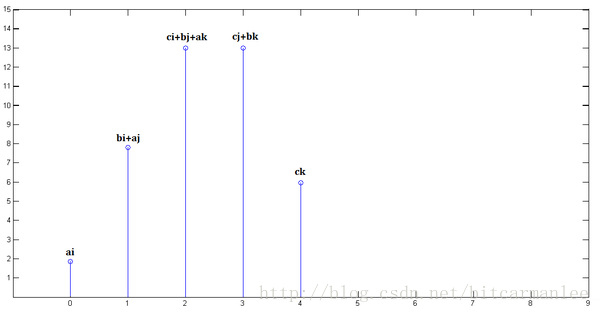
最后,把上面三个图叠加,就得到了:
无非是平移(没有反褶!)、叠加。
从这里,可以看到卷积的重要的物理意义是:一个函数(如:单位响应)在另一个函数(如:输入信号)上的加权叠加。
重复一遍,这就是卷积的意义:加权叠加
我们也可以根据公式来看,令
,
那么
,
,
,
,
。
三、卷积的应用
用一个模板和一幅图像进行卷积,对于图像上的一个点,让模板的原点和该点重合,然后模板上的点和图像上对应的点相乘,然后各点的积相加,就得到了该点的卷积值。对图像上的每个点都这样处理。由于大多数模板都是对称的,所以模板不旋转。卷积是一种积分运算,用来求两个曲线重叠区域面积。可以看作加权求和,可以用来消除噪声、特征增强。
把一个点的像素值用它周围的点的像素值的加权平均代替。
卷积是一种线性运算,图像处理中常见的mask运算都是卷积,广泛应用于图像滤波。
卷积关系最重要的一种情况,就是在信号与线性系统或数字信号处理中的卷积定理。利用该定理,可以将时间域或空间域中的卷积运算等价为频率域的相乘运算,从而利用FFT等快速算法,实现有效的计算,节省运算代价。
四、直观感受的例子
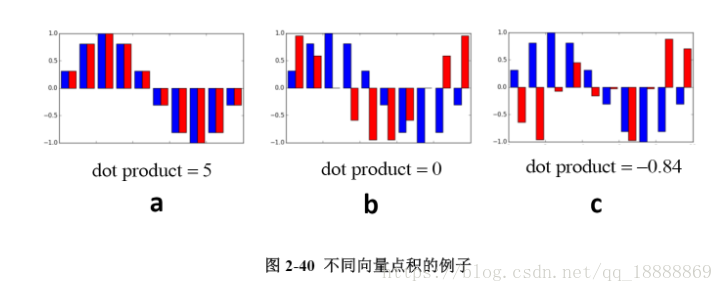
点积是计算两个向量相似性的一种重要度量。看以下例子
a中是一个形如sin的信号和本身求点积;b是sin信号和一个形如cos的信息求点积;c是该信号和一个随机产生的向量求点积。a两个信号相似程度最高,得到了最大值,c得到了负值,从视觉上看也是差异最高的。
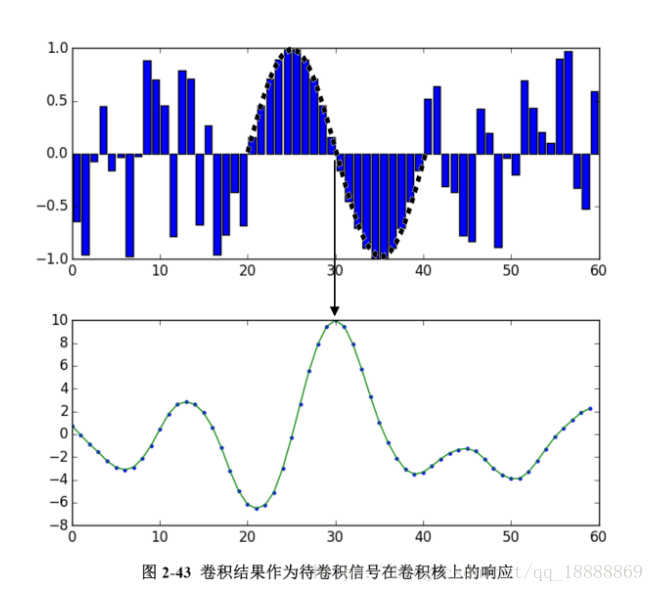
上面是一个长度为20的sin信号两边各接一个长度为20的随机信号作为一个新的带卷积信号,然后定义个倒序之后就是sin波形的信号作为卷积核。
上面是带卷积信号,下面是结果。在形如sin的信号划过被卷积信号的形如sin的区域时,卷积结果的值最大。从信号的角度,可以把卷积看做是卷积核作为一个滤波器,卷积的结果则是被卷积信号在这个滤波器上的响应。所以大体上越是和卷积核倒序之后相似的信号越是获得越大的响应。
这个例子中卷积核起到了纵向边缘查找的作用。
参考文献:
《深度学习》 Ian GoodFellow.
《深度学习与计算机视觉》 叶韵.