因研究兴趣不在图像处理,所以对图像中的『卷积』操作未做深入思考,直到某天,灵光一闪,我突然意识到
图像『卷积』应该可以和『信号处理』联系起来
更进一步
图像卷积的本质,是提取图像不同『频段』的特征
然而放眼望去,市面上大谈特谈『卷积』的文章,各种雷同,互相『借鉴』,都是在讲解卷积的不同方式、卷积的参数共享、卷积的具体操作、卷积在图像上的效果,竟鲜有一篇像样的文章,真正触及『卷积』的本质、探索『卷积』和『信号处理』的联系!
作为一个EE科班出生、当年『信号系统』『数字信号处理』课程接近满分的人,我决定剖析卷积本质,弥补市场空白!
所以本文的目的是
从信号系统角度,通俗讲解图像卷积的本质 ( 不涉及公式)
让你在面试时从容应对诸如『卷积层作用』之类的套路问题,甚至对弱鸡面试官实现反杀!
前言
因本文偏科普性质,会有失严谨性,所以在这里先补充一些信号处理的基本概念,后面章节为简化起见,将省略这些关键概念。有兴趣的读者可以深究,其他读者请直接跳过本节
一般来讲,我们涉及到的系统都是『时不变系统』(time invariant system),即 输入响应不随激励时间的改变而变化,并且是『线性系统』(linear system)。而我们所处理的时间信号一般分为四种情形:
- 连续非周期
- 连续周期
- 离散非周期
- 离散周期
这四种信号对应的频谱也是各有特点,时域的『周期』性质对应到频域是频谱『离散』,『非周期』对应『连续』,而时域的『连续』和『离散』对应到频域则是『非周期』和『周期』。图像可以看做是『离散非周期信号』(因为图像的像素点是离散的且大多没有周期性),更严谨地说,是『有限长离散非周期序列』,其频谱是连续周期性的,且z变换和傅里叶变换都存在。
说到『傅里叶变换』,其实傅里叶变换的本质是实频域分析,但对于某些信号(比如不稳定信号)并不存在这样的变换,所以更通用的做法是『z变换』,映射到复频域进行分析。更多内容,见参考资料[1]和[2]
一维信号
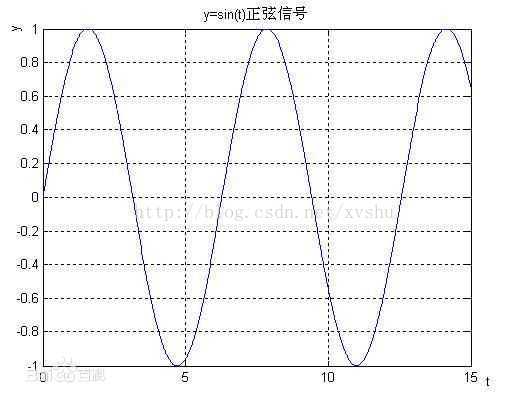
我们最常接触到的『信号』是一维时间信号,比如人的声音、乐曲、无线电波等,横坐标是时间t,纵坐标是信号的幅度,代表不同时刻的信号强度。而在教科书上,最常见的是如下正弦波
时域频域
以声音信号为例,女生的声音比男生『尖』,说白了就是『频率』更高,也就是声音信号在t轴上的『震荡』更快。而一个复杂的声音信号,通常包括很多『频段』,最直观的就是录音棚里调节各个分量的旋钮,把低频分量旋钮调高,声音更『浑厚』,有重低音的效果,而把高频分量旋钮调高,则变得尖细。
如果我们把一个信号各个频段的成分也画出来,横坐标是频段的『大小』,纵坐标是对应频段成分的『幅度』,这样一个坐标系,我们把它叫做『频域』。把信号从『时域』映射到『频域』的手段,就是大家耳熟能详的『傅里叶变换』。
不严谨地说,任意信号都可以由一组不同频率不同幅度的正弦信号叠加而成
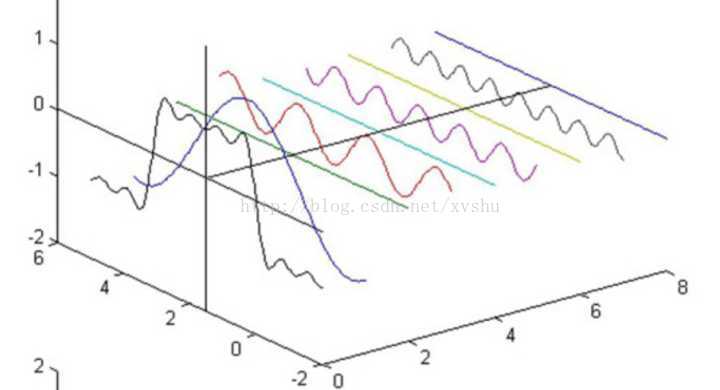
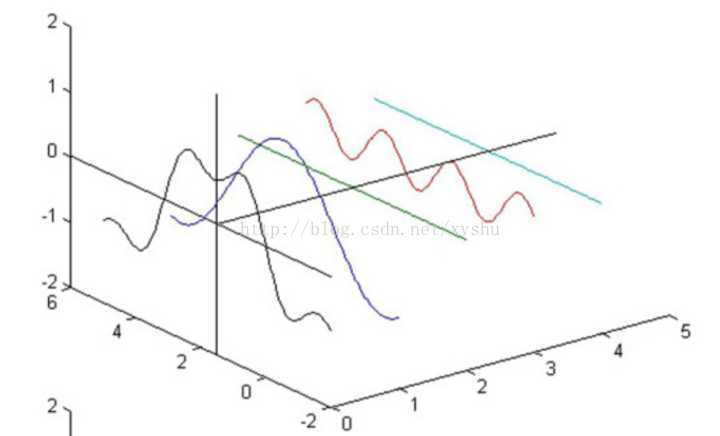
而这组正弦波,就是我们上面说的,一个信号不同『频段』的成分。更形象的图,如下所示(转载出处见水印)
给大家简单解释下这幅图,时域图像是一个典型的一维信号——一个近似的方形波,它是由一系列正弦信号叠加而成(余弦信号是正弦信号相移产生,所以是广泛意义上的正弦信号)。
卷积
卷积的概念我就不多说了,已有大把平庸的博文给大家做铺垫了。这里我只给大家提一个最最最核心的概念(也是这么多年过去了,我对信号系统留下的最最最深刻的概念)
时域卷积=频域相乘
重要的概念说三遍
时域卷积=频域相乘
时域卷积=频域相乘
这个概念的背后是一个严谨的推导过程,但这里我们略过(有兴趣的读者一定不要错过这个推导,可以阅读参考资料[1]),这里给大家通俗解释一下,假设两个时域信号f1和f2『卷积』的结果是f3,则f3的频谱,是f1的频谱函数和f2的频谱函数,对应频率『相乘』的结果
小小地拓展一下,与本文无关 这种频域相乘的特性可以用于快速求一些特定函数的积分,因为『卷积』的本质是积分,而很多特定函数存在傅里叶变换和反变换,所以与其直接求解积分函数,不如把他们变换到频域,直接进行频谱函数『相乘』,然后再反变换回来,就得到积分结果了
滤波器
滤波器这个名词想必大家也不陌生,比如带有『降噪』功能的麦克风,说白了就是把高频的噪音信号给过滤掉。更专业一点,滤波器是能过滤某些特定频段,留下需要信号的部件,比如低通滤波器(只留下低频分量)、高通滤波器(只留下高频分量)、带通滤波器(只留下特定范围内的分量)。这里就不展开讲了,免得大家回忆起那些年被『电子电路』『信号系统』等专业课所支配的恐惧。
那滤波跟卷积的有什么关系么?别忘了我们刚刚特别强调的概念
时域卷积=频域相乘
假设时域信号f1和f2做卷积,从f1的角度看,它的频谱函数要跟f2对应的频谱函数相乘,而如果f1的某些频率分量,在f2上是没有的,那么相乘之后的结果是0,所以得到的f3信号,在这些频率上值为0,于是对f1而言,f2把它的某些分量『过滤』掉了,所以f2是『滤波器』,f1是原始信号,f3是过滤之后的信号。
一个理想的低通滤波器如下所示

它的横坐标是频率,幅值为1,这是典型的『低通滤波器』,如果有信号跟它做卷积,那这个信号只会留下在0附近的低频信号,其他高频分量都被过滤掉了。
更形象一点,我们再回顾下刚刚的方波信号(注意,这里的方波信号横坐标是时间t,不是上面的低通滤波器)

它是由不同频率、相位、幅度的正弦信号组成。如果我们现在通过某种『低通滤波器』,过滤掉一些高频的正弦信号,则这个方波信号将变成下面的形状
我们发现,这个方形信号没那么『方』了,两边尖锐的『棱角』变缓和了,也没有棱角附近小幅度高频振动的波形了。我们继续加大滤波力度,将得到下面结果
我们可以看到,方形波的『棱角』基本被磨平了。所以
波形里的『棱角』其实是一种突变信号,它里面包含了很多高频分量
上面这个发现非常重要,将有助于我们后面理解图像的『卷积』和『滤波』。
二维空间
虽然我们一直在强调『时间信号』,但不知大家注意到没有,其实这里的时间t,完全可以换成其他符号比如x,从而所谓的时间信号f(t),可以写成f(x),进而,图像可以看成一个离散的二维函数f(x,y),x 和 y 决定了图像的像素点,f是像素点在该处的取值。更形象地理解,图像就仿佛是一个『水池』,像素点就是『水分子』,像素点的取值大小,从视觉上看代表图像亮度的强弱,而类比到水池里,就是不同位置水分子的运动幅度,在水池里泛起涟漪。
进而,我们很自然地想到,一维函数的『傅里叶变换』,能否扩展到二维呢?
答案是肯定的。不过二维空间的傅里叶变换公式我们就不贴出来了,大家有兴趣可以详细阅读参考资料[3]。一维函数f(x)的频谱函数F(w),是一维信号的不同频率分量,而二维函数f(x,y)的频谱函数,是一个二维函数F(w,v),也反应了二维函数的频率特性(不过理解起来不那么直观,这里略过,有兴趣的同学请阅读参考资料[2])。这里我们直接结合前面说的『滤波器』来理解卷积过程
卷积核本质上是一个二维函数,有对应的频谱函数,因而可以看成某种『滤波器』
下面是几种常见卷积核的频谱图像(摘自参考资料[4])

这是一个低通滤波器,频率接近原点附近的幅值很大(频率低的通过),越往两边越小(频率高的过滤)。下面这个高通滤波器恰恰相反
滤波器的概念有了,那么问题来了,我们该如何理解『图像卷积』和『滤波』的关系呢?
回顾下我们上节的发现——『波形里的「棱角」其实是一种突变信号,它里面包含了很多高频分量』。我们沿用上面『水池』的类比,图像像素值变化陡峭的地方,反映在图像上,就是那块区域明暗变化明显,而类比到『水池』里,就是水波在该区域快速振动,『棱角』分明。所以
当我们将图像跟『高通滤波器』做卷积时,明暗变化会被保留,而缓和的变化会被过滤
反映到图像上,就是『锐化』效果,即图像的边缘被加强,大色块的背景被过滤。同理,跟低通滤波器做卷积,效果相反。我们看看直观的效果(摘自参考资料[3])
当我们把图像跟多种卷积核作用时,就能得到不同频段的信号,这也就是卷积神经网络中,『卷积层』的本质作用。
至此,我们完美阐释了开篇提到的结论
图像卷积的本质,是提取图像不同『频段』的特征