一文搞懂交叉熵在机器学习中的使用

交叉熵（cross entropy）是深度学习中常用的一个概念，一般用来求目标与预测值之间的差距。以前做一些分类问题的时候，没有过多的注意，直接调用现成的库，用起来也比较方便。在使用交叉熵的时候，发现自己对交叉熵的理解有些模糊，不够深入。从头梳理了一下相关知识点，才算透彻的理解了，特地记录下来，以便日后查阅。

信息论

交叉熵是信息论中的一个概念，要想了解交叉熵的本质，需要先从最基本的概念讲起。

1 信息量

首先是信息量。假设我们听到了两件事，分别如下：
事件A：巴西队进入了2018世界杯决赛圈。
事件B：中国队进入了2018世界杯决赛圈。
仅凭直觉来说，显而易见事件B的信息量比事件A的信息量要大。究其原因，是因为事件A发生的概率很大，事件B发生的概率很小。所以当越不可能的事件发生了，我们获取到的信息量就越大。越可能发生的事件发生了，我们获取到的信息量就越小。那么信息量应该和事件发生的概率有关。

假设X是一个离散型随机变量，其取值集合为χ，概率分布函数 $p(x)= Pr(X=x),x∈χ$则定义事件的信息：

$I(x_0)= -log(p(x_0))$

由于是概率所以 ${p(x_0) }$ 的取值范围是[0,1],绘制为图形如下：

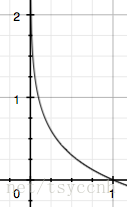
可见该函数符合我们对信息量的直觉

2 熵

考虑另一个问题，对于某个事件，有 $n$种可能性，每一种可能性都有一个概率 $p(x_i)$，这样就可以计算出某一种可能性的信息量。举一个例子，假设你拿出了你的电脑，按下开关，会有三种可能性，下表列出了每一种可能的概率及其对应的信息量

序号	事件	概率p	信息量I
A	电脑正常开机	0.7	-log(p(A))=0.36
B	电脑无法开机	0.2	-log(p(B))=1.61
C	电脑爆炸了	0.1	-log(p(C))=2.30

注：文中的对数均为自然对数

我们现在有了信息量的定义，而熵用来表示所有信息量的期望，即：
$H(X) = -\sum_{i=1}^np(x_i)log(p(x_i))$

其中n代表所有的n种可能性，所以上面的问题结果就是
$H(X) = -[p(A)log(p(A)) + p(B)log(p(B)) +p(C)log(p(C))]$
$\quad=0.7\times0.36+0.2\times1.61+0.1\times2.30 = 0.804$
然而有一类比较特殊的问题，比如投掷硬币只有两种可能，字朝上或花朝上。买彩票只有两种可能，中奖或不中奖。我们称之为0-1分布问题（二项分布的特例），对于这类问题，熵的计算方法可以简化为如下算式：
$H(X) = -\sum_{i=1}^np(x_i)log(p(x_i)) =-p(x)log(p(x))-(1-p(x)log(1-p(x)))$

3 相对熵（KL散度）

相对熵又称KL散度,如果我们对于同一个随机变量 x 有两个单独的概率分布 P(x) 和 Q(x)，我们可以使用 KL 散度（Kullback-Leibler (KL) divergence）来衡量这两个分布的差异

维基百科对相对熵的定义

In the context of machine learning, DKL(P‖Q) is often called the information gain achieved if P is used instead of Q.

即如果用P来描述目标问题，而不是用Q来描述目标问题，得到的信息增量。

在机器学习中，P往往用来表示样本的真实分布，比如[1,0,0]表示当前样本属于第一类。Q用来表示模型所预测的分布，比如[0.7,0.2,0.1]
直观的理解就是如果用P来描述样本，那么就非常完美。而用Q来描述样本，虽然可以大致描述，但是不是那么的完美，信息量不足，需要额外的一些“信息增量”才能达到和P一样完美的描述。如果我们的Q通过反复训练，也能完美的描述样本，那么就不再需要额外的“信息增量”，Q等价于P。

KL散度的计算公式：
$D_{KL}(p||q) = \sum_{i=1}^n p(x_i)log(\frac{p(x_i)}{q(x_i)})$
n为事件的所有可能性。的值越小， $D_{KL}$表示q分布和p分布越接近。

4 交叉熵

对式3.1变形可以得到：
$D_{KL}(p||q) = \sum_{i=1}^n p(x_i)log(p(x_i))-\sum_{i=1}^np(x_i)log(q(x_i))$
$\quad \quad \quad\quad=-H(p(x))+[-\sum_{i=1}^np(x_i)log(q(x_i))]$
等式的前一部分恰巧就是p的熵，等式的后一部分，就是交叉熵：
$H(p,q)= -\sum_{i=1}^np(x_i)log(q_i))$
在机器学习中，我们需要评估label和predicts之间的差距，使用KL散度刚刚好，即
$D_{KL}(y||y`)$不变，故在优化过程中，只需要关注交叉熵就可以了。所以一般在机器学习中直接用用交叉熵做loss，评估模型。

机器学习中交叉熵的应用

1 为什么要用交叉熵做loss函数？

在线性回归问题中，常常使用MSE（Mean Squared Error）作为loss函数，比如：
$loss=\frac{1}{2m}\sum_{i=1}^n(y_i-y`_i)^2$

这里的m表示m个样本的，loss为m个样本的loss均值。
MSE在线性回归问题中比较好用，那么在逻辑分类问题中还是如此么？

2 交叉熵在单分类问题中的使用

这里的单类别是指，每一张图像样本只能有一个类别，比如只能是狗或只能是猫。

交叉熵在单分类问题上基本是标配的方法

$loss = -\sum_{i=1}^ny_ilog(y`_i)$

上式为一张样本的loss计算方法，上式中n代表着n种类别。
举例说明,比如有如下样本

对应的标签和预测值

*	猫	青蛙	老鼠
Label	0	1	0
Pred	0.3	0.6	0.1

那么

$loss = -(0\times log(0.3)+1\times log(0.6)+0\times log(0.1))$
$=-log(0.6)$
对应一个batch的loss就是

$loss =-\frac{1}{m}\sum_{j=1}^m\sum_{i=1}^ny_{ji}log(y`_{ji})$

m为当前batch的样本数

3 交叉熵在多分类问题中的使用

这里的多类别是指，每一张图像样本可以有多个类别，比如同时包含一只猫和一只狗
和单分类问题的标签不同，多分类的标签是n-hot。
比如下面这张样本图，即有青蛙，又有老鼠，所以是一个多分类问题

对应的标签和预测值

*	猫	青蛙	老鼠
Label	0	1	1
Pred	0.1	0.7	0.8

值得注意的是，这里的Pred不再是通过softmax计算的了，这里采用的是sigmoid。将每一个节点的输出归一化到[0,1]之间。所有Pred值的和也不再为1。换句话说，就是每一个Label都是独立分布的，相互之间没有影响。所以交叉熵在这里是单独对每一个节点进行计算，每一个节点只有两种可能值，所以是一个二项分布。前面说过对于二项分布这种特殊的分布，熵的计算可以进行简化。

同样的，交叉熵的计算也可以简化，即

$loss=-ylog(y`)-(1-y)log(1-y`)$

注意，上式只是针对一个节点的计算公式。这一点一定要和单分类loss区分开来。

例子中可以计算为：

$loss_{猫}=-0\times log(0.1)-(1-0)log(1-0.1) = -log(0.9)$
$loss_{蛙}=-1\times log(0.7)-(1-1)log(1-0.7) = -log(0.7)$
$loss_{鼠}=-1\times log(0.8)-(1-1)log(1-0.8) = -log(0.8)$
单张样本的loss即为 $loss=loss_{猫}+loss_{蛙}+loss_{鼠}$
每一个batch的loss就是：
$loss = \sum_{j=1}^m\sum_{i=1}^n-y_{ji}log(y`_{ji})-(1-y_{ji})log(1-y`_{ji})$

式中m为当前batch中的样本量，n为类别数。

参考：

https://www.zhihu.com/question/65288314/answer/244557337
https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence
https://jamesmccaffrey.wordpress.com/2013/11/05/why-you-should-use-cross-entropy-error-instead-of-classification-error-or-mean-squared-error-for-neural-network-classifier-training/