Python金融系列第二篇：简单线性回归

作者：chen_h
微信号 & QQ：862251340
微信公众号：coderpai

第一篇：计算股票回报率，均值和方差

第二篇：简单线性回归

第三篇：多元线性回归和残差分析

第四篇：现代投资组合理论

第五篇：市场风险

第六篇：Fama-French 多因子模型

介绍

在金融和经济领域，大多数模型都是线性模型。从投资组合理论的基础到现在流行的 Fama-French 资产定价模型，我们可以看到到处都在使用线性回归。理解线性回归如何工作对理解这些理论是非常重要的。

如果我们持有股票，我们就必须对股票收益与市场回报之间的关系感到好奇。假设我们在今年的第一天购买了亚马逊股票。为了直接看到这种关系，我们在 y 轴上绘制我们的股票的每日回报，并且在 x 轴上绘制标普 500 的每日回报。

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import datetime

from pandas_datareader import data as pdr
import fix_yahoo_finance as yf

spy_table = pdr.get_data_yahoo("SPY")
amzn_table = pdr.get_data_yahoo("AMZN")

spy = spy_table.loc['2017':'2017-6',['Close']]
amzn = amzn_table.loc['2017':'2017-6',['Close']]
#calculate log return
spy_log = np.log(spy.Close).diff().dropna()
amzn_log = np.log(amzn.Close).diff().dropna()
df = pd.concat([spy_log,amzn_log],axis = 1).dropna()
df.columns = ['spy','amzn']
print(df.tail())

程序输出结果为：

                 spy      amzn
Date                          
2017-06-26  0.000658 -0.009771
2017-06-27 -0.008089 -0.017456
2017-06-28  0.008911  0.013777
2017-06-29 -0.008828 -0.014647
2017-06-30  0.001863 -0.008159

我们成功的创建了一个 DataFrame，其中包含亚马逊股票和标普 500 的每日对数回报，现在让我们来绘制这个图：

import matplotlib.pyplot as plt
plt.figure(figsize = (15,10))
plt.scatter(df.spy,df.amzn)
plt.show()

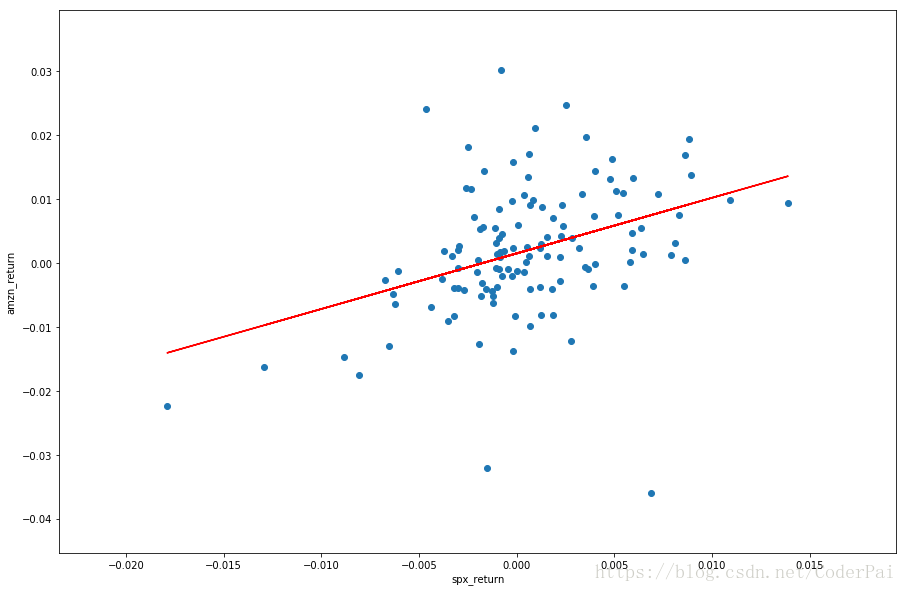
在这里插入图片描述

这是一个散点图，但是我们可以大致看到他们的相关性：通常 SPY 的每日回报越高，亚马逊股票的回报就越高。这被称为正相关。我们将在以下内容中介绍它。

斜率和截距

我们想要去模拟这两种收益之间的关系是非常自然的一件事。直观来说，我们可以使用直线来对其进行建模，这称为线性回归。为了找到最佳直线，我们很自然的认为数据集中的点和拟合线之间的垂直距离应该是最小的，那么这些垂直距离就称为残差。我们的目标是使残差平方和尽可能小。此方法称为普通最小二乘法或者 OLS 方法。我们使用 x 和 y 来表示两个变量，标普 500 每日回报和亚马逊股票每日回报。他们的线性关系如下：

$Y = \alpha + \beta * X + \varepsilon$

其中， $\alpha$ 称为截距， $\beta$ 称为斜率。更一般的来说，如果一个散点图可以表示成 ${ (x_1,y_1),(x_2, y_2),(x_3,y_3)...(x_n,y_n) }$ ，那么截距跟斜率可以如下计算：

$\beta = \frac{\sum_{i=1}^{n}(x-\bar{x})(y-\bar{y})}{\sum_{i=1}^{n}(x-\bar{x})^2}$

$\alpha = \bar{y}-\hat{\beta}\bar{x}$

其中， $\bar{x}$ 是 X 的均值， $\bar{y}$ 是 Y 的均值

在 Python 中，我们不需要手动执行上述计算，因为我们可以利用很多的开源包。但是如何理解 $\beta$ 的过程还是非常重要的，因为深入理解 $\beta$ 可以帮助我们很好的理解现代投资组合理论和CAPM，这些我们在后面的章节中都会用到。

Python 实现

在 Python 中，我们可以利用一个非常强大的数学模型包，名为 statsmodels 。

import statsmodels.formula.api as sm
model = sm.ols(formula = 'amzn~spy',data = df).fit()
print(model.summary())

程序输出结果为：

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                   amzn   R-squared:                       0.149
Model:                            OLS   Adj. R-squared:                  0.142
Method:                 Least Squares   F-statistic:                     21.43
Date:                Sat, 29 Sep 2018   Prob (F-statistic):           9.24e-06
Time:                        11:00:34   Log-Likelihood:                 403.39
No. Observations:                 124   AIC:                            -802.8
Df Residuals:                     122   BIC:                            -797.1
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept      0.0015      0.001      1.782      0.077      -0.000       0.003
spy            0.8699      0.188      4.629      0.000       0.498       1.242
==============================================================================
Omnibus:                       24.014   Durbin-Watson:                   1.960
Prob(Omnibus):                  0.000   Jarque-Bera (JB):              104.250
Skew:                          -0.472   Prob(JB):                     2.30e-23
Kurtosis:                       7.392   Cond. No.                         222.
==============================================================================

我们使用 statsmodels 中的 OLS() 函数构造了一个简单的线性回归模型。model 实例有非常多的属性。最常用的是参数，斜率和截距。我们可以通过以下方式访问他们：

print("parameters: ", model.params)
[out]:
parameters:  Intercept    0.001521
spy          0.869893
dtype: float64

print("residual: ", model.resid.tail())
[out]:
residual:  Date
2017-06-26   -0.011864
2017-06-27   -0.011940
2017-06-28    0.004505
2017-06-29   -0.008489
2017-06-30   -0.011300
dtype: float64

print("fitted values: ", model.predict())
[out]:
fitted values:  [ 6.68050054e-03  8.29306401e-04  4.62741717e-03 -1.35551546e-03
  1.52067302e-03  3.97561282e-03 -6.65450265e-04  3.51524155e-03
 -1.54977769e-03  3.44096707e-03 -1.70783245e-03  4.71083520e-03
 -7.45869239e-04  7.08038453e-03  9.01766774e-03  6.10762024e-04
  1.54048450e-04 -3.89092003e-03  1.44419603e-03  1.86467905e-03
  2.09377255e-03  7.49617233e-03 -3.58738146e-05  1.55870750e-03
  2.65983467e-03  6.66619420e-03  4.94666869e-03  6.24229007e-03
  4.98925643e-03  6.05002623e-03  7.79782437e-04  2.89082766e-03
  6.68569923e-03  7.47851776e-04  2.10954612e-03  2.62372277e-03
  2.87914582e-03 -8.30487212e-04  1.36125978e-02 -3.97472616e-03
  2.06810897e-03 -1.07364762e-03 -1.08146394e-03 -9.58279135e-05
  2.62316360e-03  4.56361219e-03  1.95971780e-03 -1.81444385e-03
  9.01586717e-03 -1.92042314e-04 -3.78456096e-03  5.65977433e-04
 -9.72063837e-03  3.56526159e-03  5.91915424e-04  8.88557784e-04
  6.27462258e-04  7.82781226e-03  2.33350159e-03  4.28616147e-03
 -5.06446730e-04  6.42104156e-06  2.07494597e-03 -1.06905521e-03
  3.96264845e-03  6.33459517e-04  2.03831009e-03  4.85090670e-04
 -2.29944688e-03 -4.14763216e-03  9.19388548e-03 -1.07917356e-03
 -8.01815000e-05  8.57216909e-03 -1.25599671e-03  1.10354583e-02
  6.56759032e-03  9.73479825e-04  2.25018748e-03 -3.77238249e-04
  3.71015212e-03  1.84866735e-03  4.63464465e-04  2.54141298e-03
  4.93873293e-03  1.37552168e-03  7.21768822e-04  3.08144854e-03
 -2.58102781e-04  6.58474249e-05  6.31230982e-03  7.23897547e-04
 -1.40533454e-02  5.01798209e-03  7.16028672e-03  5.92633377e-03
  3.44340518e-03  3.54762800e-03  5.66841594e-03  1.34078999e-03
  7.64548981e-04  1.30453252e-03  8.41094284e-03  4.41120996e-03
  8.79185196e-04 -1.26469613e-03  3.12869665e-03  1.94896326e-03
  1.99397262e-04  1.34195495e-03  5.76398290e-03  4.17276093e-04
 -1.54910762e-04 -2.52112272e-03  8.73264647e-03 -4.36583488e-03
  1.30587572e-03  1.12672194e-03  2.55891155e-03  2.09290596e-03
 -5.51573435e-03  9.27193803e-03 -6.15848801e-03  3.14107759e-03]

现在让我们来看看我们的拟合线：

在这里插入图片描述

红线是拟合的线性回归直线。我们可以看到汇总表中有很多统计结果。现在让我们谈谈一些重要的统计参数。

模型意义

平方误差之和（SSE）用于测量拟合值与实际值之间的差异，具体公式如下：

$SSE=\sum_{i=1}^{n}(y_i-\hat{y_i})^2=\sum_{i=1}^{n}\hat{\epsilon _{i} ^{2} }$

如果线性模型完全符合样本，那么 SSE 的值将是零。我们在这里使用平方误差的原因是，如果我们简单的将他们相加，则正负误差将互相抵消。对样本的另一种测量称为总平方和，或者 SS，它的公式如下：

$SS=\sum_{i=1}^{n}(y_i-\bar{y_i})^2$

如果你熟悉方差，那么我们可以看到 SS 除以样本数 n 就是样本方差。从 SSE 和 SS，我们可以计算确定系数，或者称为 r 平方。r 平方是指由 X 和 Y 之间的线性关系的变化比例，它的计算公式如下：

$r^2=1-\frac{SSE}{SS}=1-\frac{\sum_{i=1}^{n}(y_i-\hat{y_i})^2}{\sum_{i=1}^{n}(y_i-\bar{y_i})^2}$

让我们假设模型完美的拟合了样本，这也就意味着样本点都是位于直线谁给你，然后 SSE 将变为零，并且 r 平方将变为 1，这意味着完美的适应性。r 平方越高，表示样本点的拟合程度越高，这也可以看出模型的重要性水平。