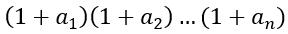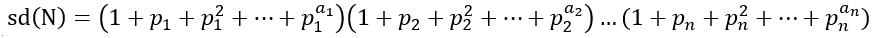线性筛

线性筛可以筛出一堆积性函数,逐一复习一下.

莫比乌斯函数

定义: $\mu(1)=1,若n可以分解为k个互异素数的乘积,则\mu(n)=(-1)^k,其他情况,\mu(n)=0$
在线性筛中,每个数都只会被它最小的质因数所筛到.
质数的莫比乌斯函数显然为-1
所以当 i%prime[j]==0 时,n已经有两个prime[j]的质因子,所以 $\mu(i*prime[j])=0$ .
另一种情况i%prime[j]!=0,相当于对在当前i的基础上又多了一个质因子,所以 $\mu(i*prime[j])=-\mu(i)$

欧拉函数

定义: $\phi(n)为小于n的,与n互质的数的个数$
当p为质数时, $\phi(p)=p-1$
当i%prime[j]==0, $\phi(i*prime[j])=\phi(i)*prime[j]$
当i%prime[j]!=0, $\phi(i*prime[j])=\phi(i)*\phi(prime[j])=\phi(i)*(prime[j]-1)$

约数个数

筛约数个数时,需要要个辅助数组,储存最小质因子的个数.

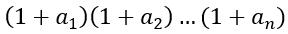
当i为质数时, $d[i]=2,num[i]=1$
当i%prime[j]==0, $d[i*prime[j]]=d[i]/(num[i]+1)*(num[i]+2),num[i*prime[j]]=num[i]+1$
当i%prime[j]!=0, $d[i*prime[j]]=d[i]*(prime[j]+1),num[i*prime[j]]=1$

约数和

约数和
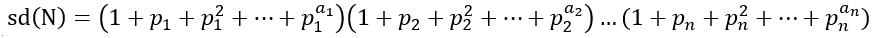
则需要的辅助数组为最小质因子对答案的贡献.
当i为质数时, $sd[i]=i+1,f[i]=i+1$
当i%prime[j]==0, $sd[i*prime[j]]=sd[i]/f[i]*(f[i]*prime[j]+1),f[i*prime[j]]=f[i]*prime[j]+1$
当i%prime[j]!=0, $sd[i*prime[j]]=sd[i]*sd[prime[j]],f[i*prime[j]]=prime[j]+1$

整体实现代码

拓展欧几里得及裴蜀定理

欧几里得算法

略

拓展欧几里得

求解不定方程: $ax+by=gcd(a,b)=1$
首先通过拓欧求得一组特解 $(x0,y0)$
这里写图片描述
然后可得通解 $x=x0+(b/d)*k,y=y0-(a/d)*k$

void exgcd(int a,int b,int &d,int &x,int &y){
    if(!b){
        d=a,x=1,y=0;
        return;
    }
    int xx,yy;
    exgcd(b,a%b,d,xx,yy);
    x=yy;
    y=xx-a/b*yy;
}

如果上述方程中的a,b不互质,则我们尽可能地将它们转为互质的.
这里写图片描述

扫描二维码关注公众号，回复： 3545469 查看本文章

拓欧的主要应用在(一)不定方程(二)模线性方程
例题:BZOJ-1407
枚举答案m进行验证.
对于每两个野人,它们不冲突当且仅当 $c[i]+x*p[i] \equiv c[j]+x*p[j](mod m)$ 无解,或者最小整数解大于min(l[i],l[j])
Code
习题:HDU-1211

裴蜀定理

裴蜀定理的内容:

设 a,b是不全为零的整数, 则存在整数 x,y 使得 $ax+by=gcd(a,b)$
另一种说法不定方程 $ax+by=m$ 有整数解,当且仅当 $m是gcd(a,b)的倍数$

感觉这个东西应该在拓欧的时候说,但还是有些关于裴蜀定理的题

例题1:BZOJ-2257
题中的第三个操作得到的容量相当于 $ax+by$ ,因为x,y都是整数,由裴蜀定理,所以容量都是 $gcd(a,b)$ 的倍数,又因为火星人会操作到尽可能小,最终的答案就是最大公约数.
那么问题也就转换为了在n个数中选k个,使得这k个数的最大公约数最大.
Code

例题2:CodeForces - 510D
假设我们只有两种卡片,那么想要使得每一个格子都到达则可以看作满足 $ax+by=1$ ,由裴蜀定理可得,当且仅当a,b互质的时候满足条件.那么相当于我们要找一条从0开始,到1结束的最短路.边为卡片上的数和当前的数取最大公约数,费用为卡片的费用.用优先队列优化的dj即可.
Code

例题3:BZOJ-2299
如果我们将这种操作进行分类,则可以看为若干次 $x\pm2*a和x\pm2*b$ 以及若干次 $y\pm2*a和y\pm2*b$ 和最多各一次的 $x\pm a,y\pm b$ .
因此我们只需要枚举后面两种操作的出现情况,然后利用裴蜀定理判断.
即 $2*a*p+2*b*q=x,2*a*q+2*b*p=y(注意这里的x,y是枚举后两种操作之后得到的)$ 是否有解即可.
Code

总结
裴蜀定理虽然听上去是个新名词,可是我们已经将它运用过很多次了,不需要重点关照,按照平时的思路直接做即可.

2018NOIP知识梳理(二)——数论相关(一)

线性筛