本博客中 PGM 系列笔记以 Stanford 教授 Daphne Koller 的公开课 Probabilistic Graphical Model 为主线,并参阅 Koller著作及其翻译版对笔记加以补充。博文的章节编号与课程视频编号一致。
博文持续更新(点击这里见系列笔记目录页),文中提到的资源以及更多见 PGM 资源分享和课程简介。
本文围绕马尔可夫网(MNs),讨论三方面内容:
1)MNs 的模型:成对马尔可夫网,吉布斯分布,条件随机场,对数线性(Log-Linear)模型,伊辛(Ising)模型,度量马尔可夫随机场。作为模板的共同特征提取。
2)MNs 的结构:独立关系,因子分解,以及两者等价性。BNs 和 MNs 的相互转化,概率图统一的双重对偶视角,I-map,P-map 的存在唯一性,通过图完美捕捉分布中的所有独立性。
3)MNs 的应用:详解 CRFs 应用的建模思路和方法分析:图像去噪,图像分割,三维重建,自然语言处理。
1 成对马尔可夫网
1.1 形式化表示
- 成对马尔可夫网 ( Pairwise Markov Networks ) : 一个以随机变量
Xi 为节点无向图网络,每一条边代表一个因子ϕij(Xi,Xj) .
它是马尔可夫网中最简单的一种,是因子定义在成对变量上的分布。
1.2 简单例子
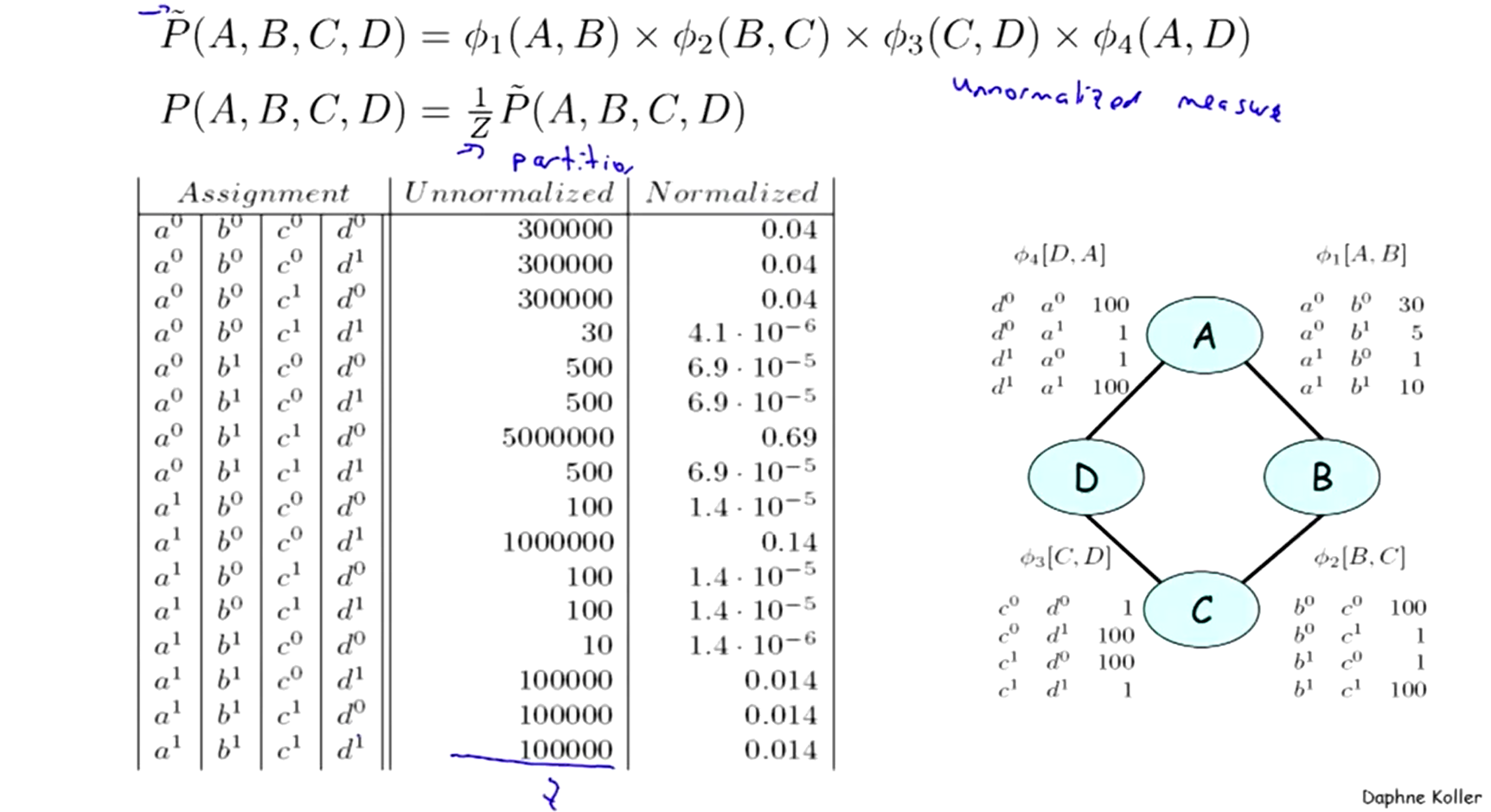
右下图表示了一个由四个随机变量
1.2.1 联合分布
左上图是由所有(四个)因子相乘计算得到的右上图例子的联合分布表。表中“unnormalized”列的因子积是未经过归一化的,所以这些值只是因子积,还不算是严格意义上的一个分布表示。
1.2.2 配分函数
为了进行归一化,计算上图例子中的配分函数(partition function)
1.3 如何理解因子
1.3.1 因子和什么有关
在成对马尔可夫网中,从因子能否看出其分布的独立性?能否尝试将因子理解为变量在其辖域上的边缘分布?
如果这样,我们通过观察任何一个因子,都有可能相信由马尔可夫网定义的整体联合分布与因子定义的分布有相似的特性(比如某两变量间边上的因子很小,那么这两个变量倾向于边缘独立)。
然而答案是否定的:

答案是和以上三个都无关,所以因子的特殊含义就是本文马尔可夫网要讲的内容。
1.3.2 从因子到联合分布
下面我们继续上文的例子,来解释:为何难以将边缘独立性和因子关联起来?
- 边缘分布:划掉某些因子后考虑剩余因子上的联合分布,即为剩余因子的边缘分布,如左下表1。
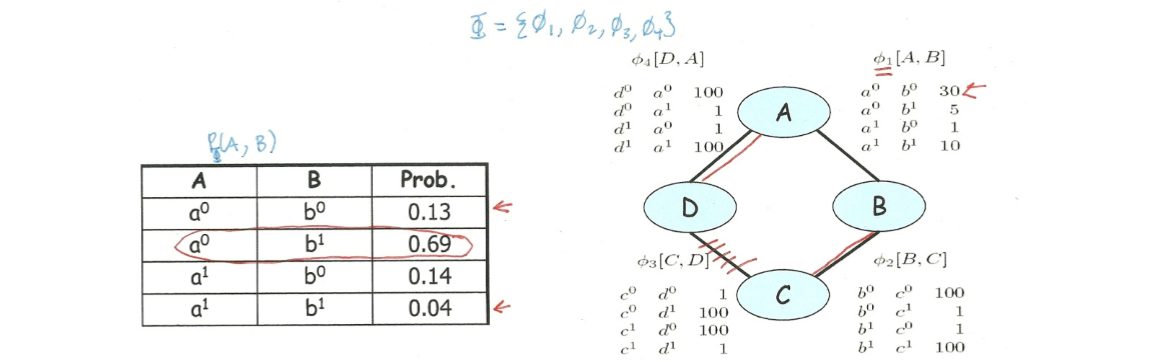
如上左图为计算得
通过这个例子需要明确,一个因子仅仅是影响联合分布的一个因素,而作为网络整体的联合分布必需将所有因子的影响考虑进去。网络的联合分布是所有因子共同作用产生的结果。
1.4 更大的网络例子
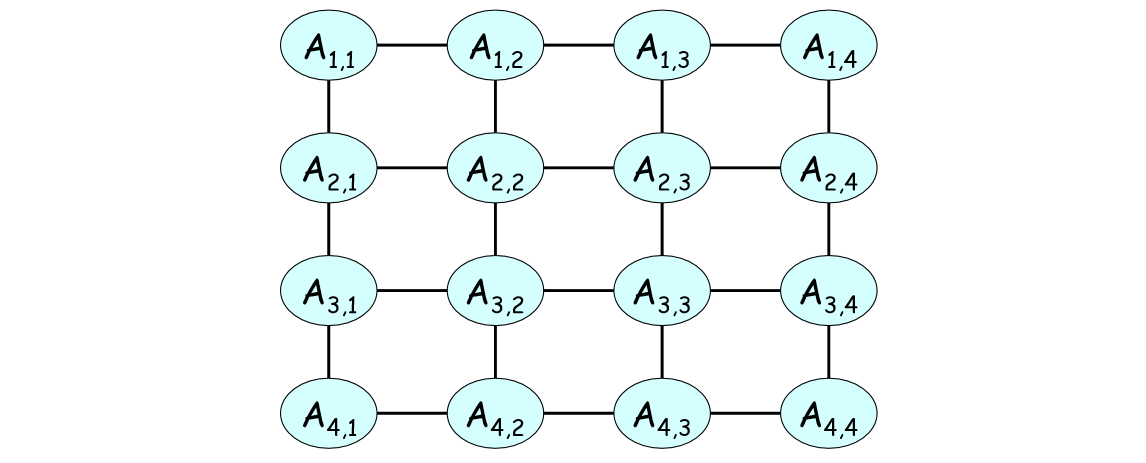
值得一提的是,是否是成对马尔可夫网由因子的选取决定。比如下图,只要我们将因子选取在成对变量上,它就是一个更大的成对马尔可夫网例子。
2 吉布斯分布
2.1 成对马尔可夫网的局限
成对马尔可夫网不能表示变量的所有组合:表示一个
所以不是每一个分布都可以表示为成对马尔可夫网。
2.2 形式化表示
这里给出马尔可夫网的形式化描述,可以先不详细看。对于一个以随机变量
- 变量集:网络中的随机变量被划分为多个变量集,记作
Dk={Xk1,...,Xklk} . - 因子 ( factor ):因子
ϕ 是定义在随机变量集合D 上值域为实数的函数,通常我们关心非负因子; - 辖域 ( Scope ):变量集
D 称为因子ϕ 的辖域。记作Scope[ϕ] ; - 因子乘积: 将两个有公变量的变量集按其公共变量的统一属性对应的因子做乘积,如
ψ(X,Y,Z)=ϕX,Y(X,Y)ϕY,Z(Y,Z) . - 因子的联合分布:因子的联合分布由其辖域上的因决定,即
ϕk(Dk)=∏l=1lkϕl(Xl) . - 网络的联合分布:马尔可夫网的联合分布由其所有因子的联合分布
ϕk(Dk) 之积决定,即PΦ(X1,...,Xn)=∏k=1mϕk(Dk) .
可以看到,上述我们得到的网络联合分布概率的表示,在严格意义上还不是一个分布,因为这个概率之和不一定为 1,所以这里需要对网络进行归一化。我们定义
- 配分函数 ( partition function ):用于联合分布表示中的归一化参数,即
Z=∑X1,...XnP˜Φ(X1,...Xn)
现在我们可以给出上述马尔可夫的网联合分布一个严格表示
2.3 吉布斯分布
式 (1) 所表示的分布被称作一个被因子集
与成对马尔可夫网这种因子定义在成对变量上的马尔可夫网相比,可以将吉布斯分布直观理解为
- 吉布斯分布 :是马尔可夫网中因子定义在变量集的分布。
并且吉布斯分布将分布表示为了因子的乘积,提出了一种对于分布的分解表示方式。
2.4 由因子导出图
既然网络联合分布由因子决定,而吉布斯分布是因子定义在变量集上的分布。那么,是否可以由吉布斯分布的因子来推出其相应图的结构呢?
如图,给出两个因子,其导出的马尔可夫网络(Induced Markov Network)如右图。
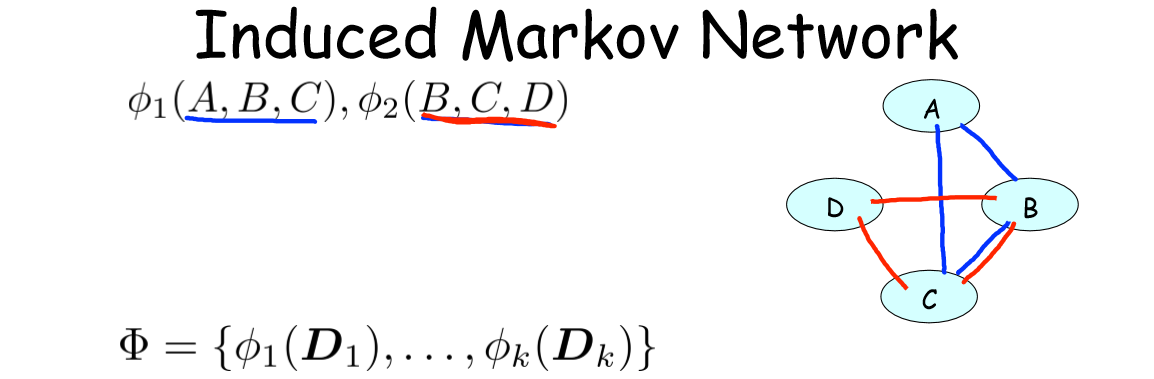
一般地,给出如上因子集,和其对应的一组随机变量
2.5 因子分解
对于给定的一个分布
- 因子分解:如果存在一个因子集
Φ=ϕ1(D1),...,ϕK(DK) 使得PΦ=P ,则称分布P 可以由马尔可夫网H 因子分解。
2.6 从图到因子分解
现在反过来考虑,给定一个吉布斯分布对应的图,是否可以推出其因子集(因子分解)?

答案是“All of above”,即从图读不出因子分解,即马尔科夫网的结构不能完全地刻画(fully specify)出分布的特性。
我们看到,不同的吉布斯分布(和其对应的因子分解)可能导出相同马尔可夫网络(Induced MN)图,且这些图性质无差别。即吉布斯分布的表达能力(expressive power)要强于图结构的表达能力。
这很好理解,前文 2.1 部分已经阐述了成对马尔可夫网的所能表达的分布个数远小于实际网络可能的分布个数,而这里的成对马尔可夫网实际上和导出图的结构一一对应(成对 MN 的因子与导出图的边一一对应)。
注:“图的结构”怎么理解?由于马尔可夫网是无向图,所以图的结构就完全有图中的边来决定。两个节点相同的图(随机变量一定),边一一对应则两图结构相同。
2.7 影响的流动 ( Flow of Influence )
同贝叶斯网一样,马尔可夫网中也存在节点间影响的流动,而且这里的 Flow 似乎更自由。
由于是无向图,故当所有节点均未被观测时,影响的流动与节点类型无关(即不区分有向图中的父子节点),只要两节点间存在路径(迹),影响就可以流动。当有部分节点被观测时,只要两个节点间某一条迹上节点均未被观测,该迹上仍可以有影响力流动,并称该迹是激活(active)的。
- 若节点均未被观测,影响可以在任何迹中流动。
- 若有节点被观测了,影响可在激活的迹中流动。
即马尔可夫网中影响沿着任何无向迹流动,仅当我们对迹中某些节点取条件时,流动才会受到阻碍。
2.8 重点总结
- 吉布斯分布将分布表示为了因子的乘积;
- 由因子导出的马尔可夫网中,属于同一辖域的变量两两之间有边连接;
- 马尔可夫网的结构不能完全地刻画出分布的特性;
- 马尔可夫网中影响沿着任何无向迹流动,仅当我们对迹中某些节点取条件时,流动才会受到阻碍。
3 条件随机场
条件随机场(CRF, Conditional Random Fields)与马尔可夫网(MN, Markov Network)结构类似,但目的不同,它采取与吉布斯分布不同的配分函数去归一化分布。
3.1 朴素贝叶斯网的不足
当一个问题的 features 为
为了弥补这点,条件随机场(CRF)将所有 feature(已知或未知)整体看作是马尔可夫网(MN)的变量,两两之间都可以相关。对问题的求解转化为求解这个网络分布在
3.2 形式化表示
条件随机场即为观察到了一些(已知)变量的马尔科夫网,该马尔科夫网剩下(未知)变量的条件概率的公式化表示即为条件随机场的公式化表示。该模型可以忽视观察变量之间的相关性,因为它们已经被观察到了。其与吉布斯分布的区别在于归一化方式不一样,这是由于 CRF 的归一化因子中的观察变量是常量2。
具体来说, CRF 的形式化表述为(符号同吉布斯分布,故不赘述):
对于一个有因子集
3.3 CRFs and Sigmoid Model
模型中有二值证据变量
-
Y 为 1 时Φ(Xi,Y=1)=exp(wiXi) -
Y 为 0 时Φ(Xi,Y=0)=1
从而可以判断
-
P˜Φ(Xi,Y=1)=exp∑i(wiXi) -
P˜Φ(Xi,Y=0)=1
从而其配分函数为
从而得到条件分布为 Sigmoid 函数
3.4 CRF 的应用3
(1) 图像分割:用于超级像素分类,而不论其采用了何种特征、特征之间是否有关系。
(2) 自然语言处理:给句子中的词打标签,其特征可以是:首字母是否大写,词语的位置,前后词等。
4 马尔可夫网中的独立性
因子分解将分布被表示为因子之积,这与该分布蕴含的独立关系之间有着复杂联系,这是概率图模型最优美的性质之一。
这部分讨论马尔可夫网中的独立性( Independencies in MNs ),类似贝叶斯网中的讨论(点击这里),给出考察图结构的两等价观点(双重对偶视角):因子分解和独立性关系。
4.1 分离
前文这里定义激活的迹(active trial)为:迹中所有节点均未被观测。现在在马尔可夫网
- 分离:节点
X 与Y 之间没有激活的迹,则它们是分离的。记作sepH(X,Y|Z) 。
注:分离概念的英文陈述:
4.2 独立性
分离的性质是否可以给出一个分布中的独立性信息呢?具体地,当分布
- 定理(独立性): 节点
X 与Y 是分离的,则它们是独立的。
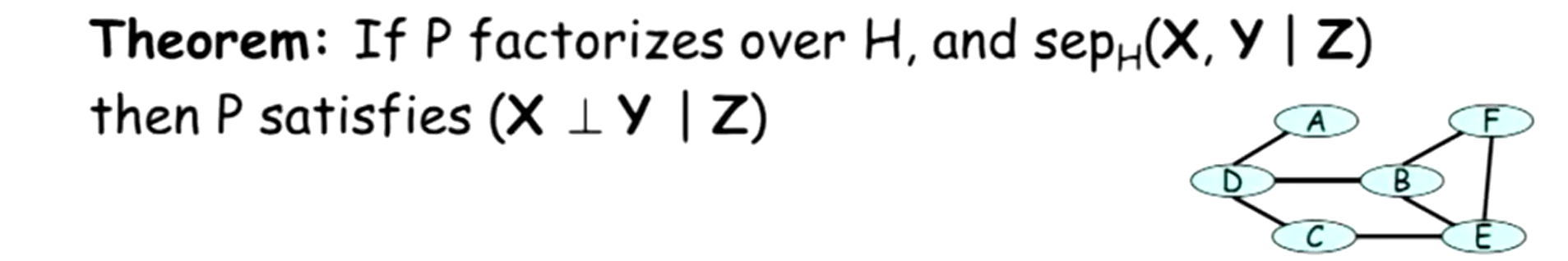
如图为独立性的形式化表述。右上图的例子中,以下几种情况下都满足
1)
4.3 图结构的两等价观点
类似博文(点击这里)中贝叶斯网中的讨论,对于马尔可夫网
-
H 导出的独立性集合:I(H)={(X⊥Y|Z):sepH(X,Y|Z)} - I-map:如果分布
P 满足I(H) ,即I(H)⊆I(P) ,称H 为分布P 的 I-map(Idpendence Map)。
一个分布的 I-map 体现了该分布中蕴含的独立性。以下介绍两个关于 I-map 的可靠性定理。
设P是一个分布,H是一个马尔科夫网结构,则:
1)如果
2)如果
注1:这两个定理的英文陈述如下
1)If
2)Hammersley Clifford th:For a positive distribution
注2:正分布即因子均为正数的分布。
至此,类似贝叶斯网络中的讨论,我们得到了描述图结构的两种等价性观点:
至此,我们得到一个分布的因子分解对应于该分布蕴含的独立性关系。
5 I-maps and Perfect Maps
5.1 从图中捕捉分布的独立性?
同贝叶斯网中的讨论(点击这里)一样,前文我们在马尔可夫网中得到了相同的等价观点。结合起来就是概率图的双重对偶视角:
-
P 在图G 上因子分解⟺ G 是P 的一个 I-Map
而
-
G 中蕴含的所有独立性关系都包含在P 中
但反之未必(not always vice verse),即分布
5.2 稀疏图
若从图中读不出分布的所有独立性,这有什么不利的影响呢?
事实上,包含独立性信息越少的图通常包含更多边,使得建模的过程不必要地冗杂。一般地,如果一个图
- 越稀疏(sparser,fewer parameters,fewer edges)
- 传递了更多的信息量(more informative)
所以对于一个分布
5.3 最小 I-map
如何寻找上述的体现分布中更多独立性的稀疏图?
我们知道,冗余边通常导致着更少的独立性,所以如下定义最小 I-map ( Minimal I-map),试图捕获分布中更多的独立性。
- 最小 I-map:没有冗余边的 I-map,即去掉任何一条边,则图无法满足分布的某些独立性关系。
但最小 I-map 的定义不是完美的(may still not capture

左图显然;我们来考察右图,首先由于
- 去掉
D→G :则有(D⊥G) ; - 去掉
G→I :则有(G⊥I|D) ; - 去掉
D→I :则有(D⊥I|G) 。
这三个独立性断言都这不属于
5.4 完美图
5.4.1 P-map 的定义
是否有图可以完美捕捉分布中的独立性呢?(对于贝叶斯网 BN 和马尔可夫网 MN)我们定义:
- 完美图(Perfect Map): 图
G 导出的独立性集合与分布P 对应的独立性相等,即I(G)=I(P) ,称G 为P 的完美图。
这样的图
- 经常会不存在 P-map;
- 有时存在多个 P-map 。
接下来举例说明有些分布不存在作为 MN 或 BN 的 P-map,并讨论 P-map 不唯一的例子。
5.4.2 BN 不存在 P-map 的例子
- 例1:分布是
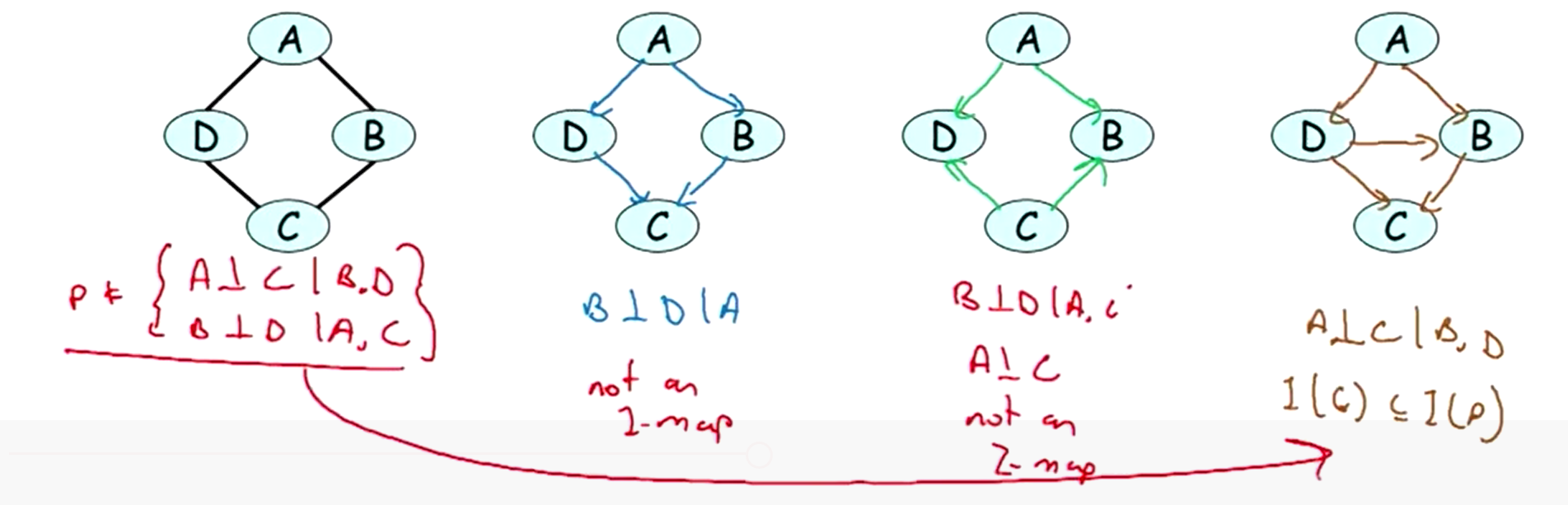
I(P)={(A⊥C|B,D),(B⊥D|A,C)} 。
记上图分别图1, 2, 3, 4。图1是
- 例2:分布如下图右表所示,
Y 是关于X1,X2 的异或函数(XOR)。
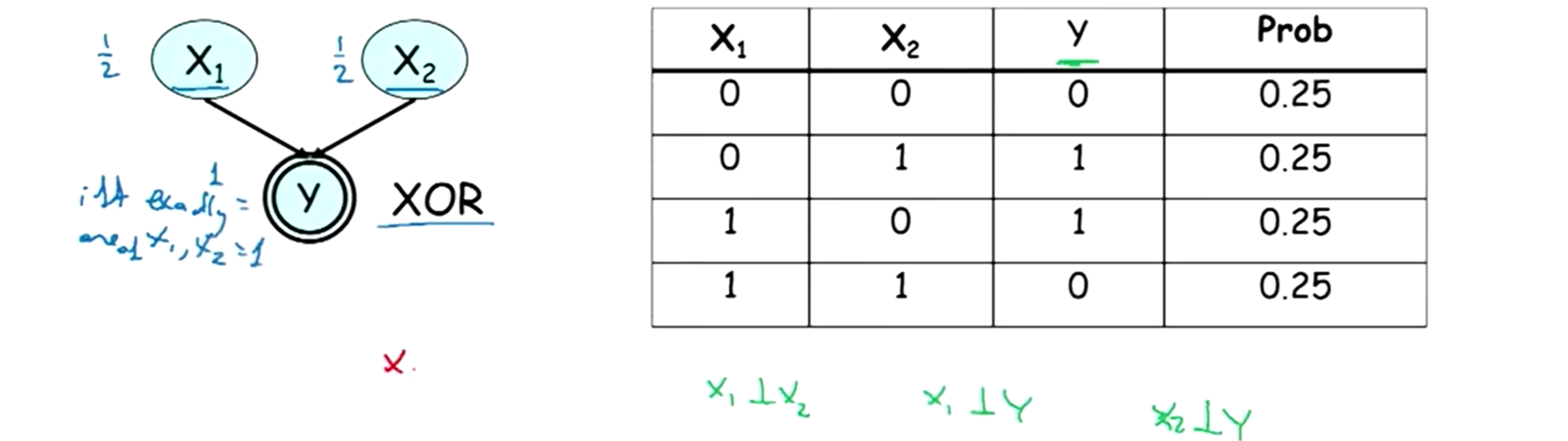
从联合分布表中可以读出
以上两个例子均不存在作为 BN 的P-map。
5.4.3 MN 不存在 P-map 的例子
左图是
故这个例子均不存在作为 MN 的P-map。
5.4.4 P-map 的不唯一性
现在举例说明 P-map 的不唯一性。分布

5.5 I-等价
如何理解
- I-等价(I-equivalence): 如果两个图的独立性集合完全相同,即
I(G1)=I(G2) ,则称这两个图是 I-等价的。
可以看到,前一例中的三种结构彼此 I-等价,它们分别是为贝叶斯网络的因果迹、证据迹与共同原因迹。 注意大多数图都有很多与其 I-等价的图。
5.6 重点总结
1)捕捉分布中独立性的方法
这部分我们一直在努力对给定分布寻找一个图,使得该图可以捕捉到该分布中的所有独立性。讨论到了两种尝试,分布是 I-map 和 P-map,两者各有优劣,且都没能完美地解决问题我们的问题。
- I-map:虽然 I-map 一定存在,但 I-map 无法捕捉分布中的所有独立性;
- P-map:虽然 P-map 捕捉了分布中的所有独立性,但 P-map 经常不存在。
2) 从分布构建图
通过分布构建网络图时候,我们可以把每个节点写成因子的形式,然后根据因子关系构建相应网络。即借助节点与其父节点,子节点的关系构建网络的结构。比如 BN 有由父节点指向子节点的有向边,比如 MN 中有边连接的两节点是不独立的。
3)MN 和 BN 的转换
前文例子涉及到了很多贝叶斯网和马尔可夫网之间的转化。但事实上,在 MN 和 BN 的转换过程中,很多独立性关系流失掉了。
(1)BN 转 MN:会损失 V-结构中的独立性关系;
(2)MN 转 BN:需要在环状结构中添加边以构成三角形。
6 对数线性模型
局部结构(local sturcture), 即课程第 05 部分(点击这里)所讨论的条件概率分布(CPD),可以通过条件概率表格(CPT, Conditional Probability Table)来表示,而不需要列出整个联合分布表(full table)。CPDs 在概率图(MNs 和 BNs)模型中十分重要。在 MNs 中,可以选择对数线性模型来体现网络的局部结构。
6.1 形式化表示基于特征的模型
对数线性模型中(Log-Linear Model),对于一个分布
- 特征集:
F={f1(D1),...,fk(Dk)} - 系数:
ω1,...,ωn
吉布斯分布中,整体分布的概率由因子之积
6.2 表格因子的表示
给定一个吉布斯分布中的因子,它定义在二值随机变量
6.3 语言处理中的特征选取
以语言处理为例,建立对数线性条件随机场模型,目的是辨别句子中单词的类型标签(地名,人名,其他)。
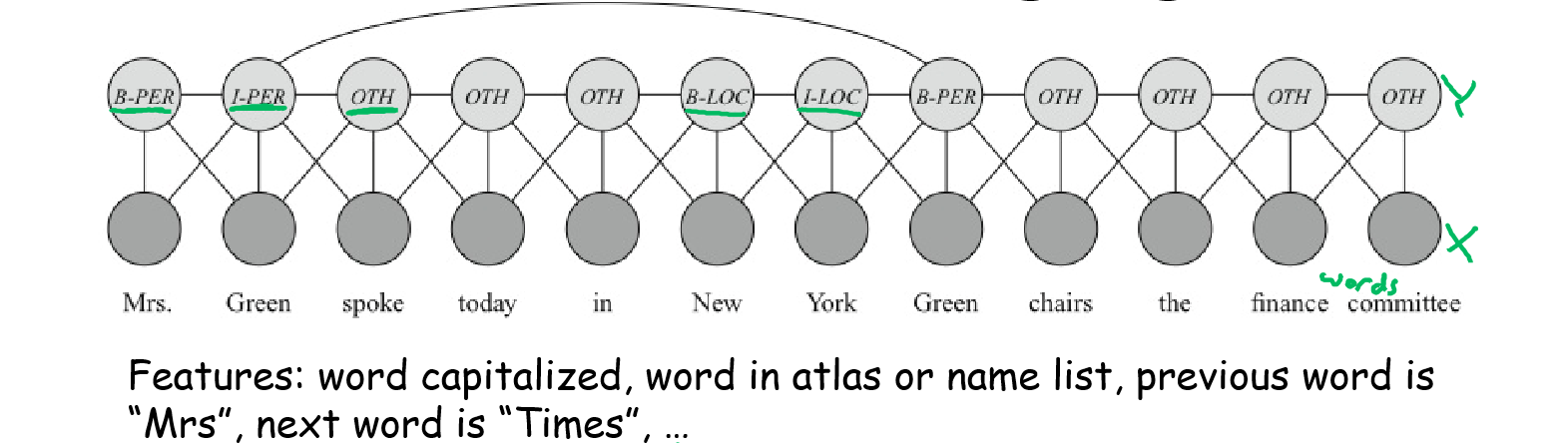
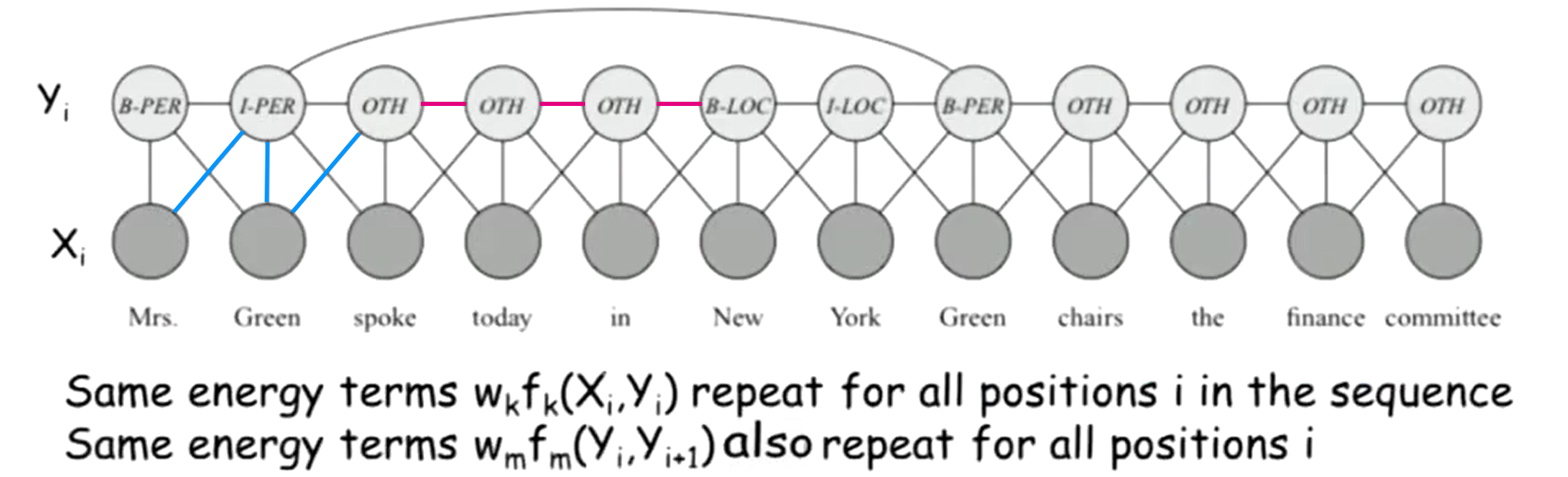
一句话被划分为单个词, 两组随机变量
- B-PER:人名的开始(Beginning of a person’s name)
- I-PER:人名的持续(Continuatoin of a person’s name)
- B-LOC:地名的开始(Beginning of a location)
- I-LOC:地名的持续(Continuatoin of a location)
- OTH:其他(Other)
用 Log-Linera Model 建模,需要在辖域
1)
2)
3)
通过系数
模型通过选取一组丰富的特征函数,分别考察单词某个特定方面的特征,并给不同特征分配权重,综合作为分类依据。而不需要列举每个单词,分别估算其作为人名,地名,或其他的概率有多大。
6.4 伊辛模型
伊辛模型(Ising Model)是一个 pairwise 马尔科夫模型,出现于统计物理学,作为原子相互作用的物理系统的能量模型。
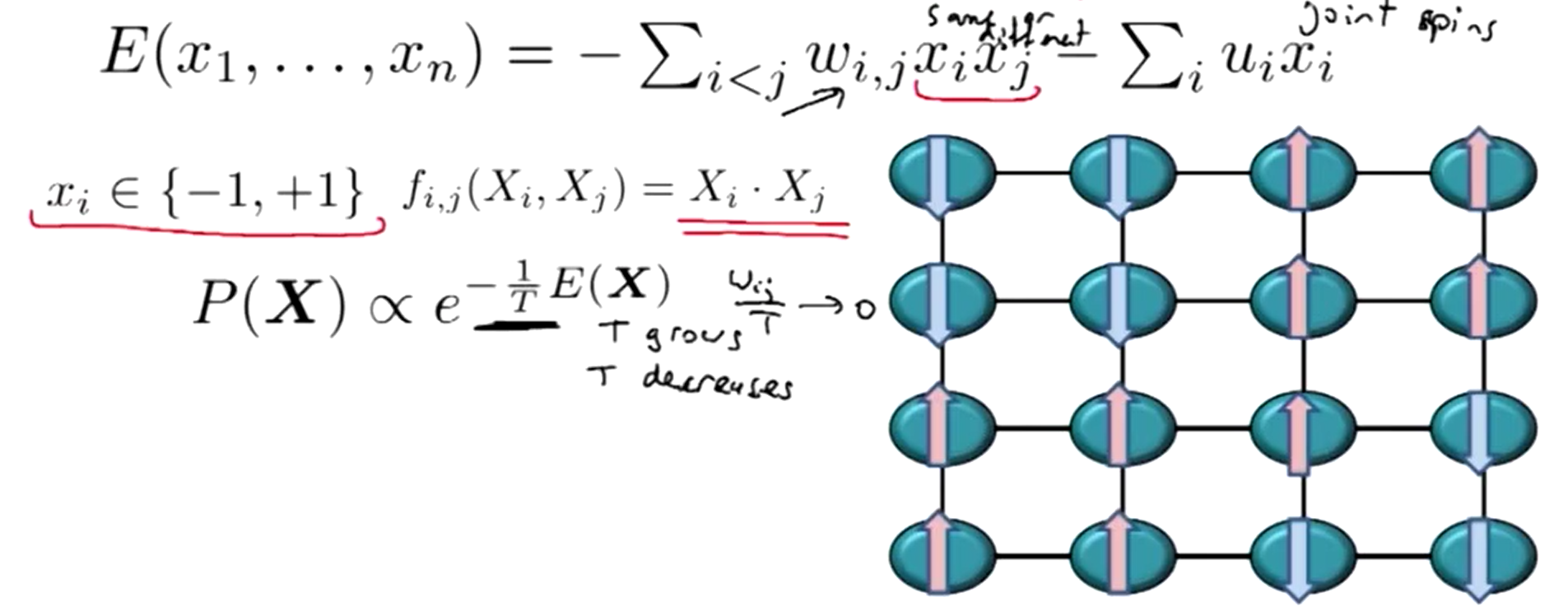
当
记系统温度参数为
6.5 度量马尔科夫随机场
度量马尔科夫随机场(Metric MRFs)中定义了度量空间和距离函数的概念。
- 假设:所有的变量的在同一空间 V 中取值(all
Xi take values in label space V) - 目标:使变量间取值尽可能相近(want
Xi,Xj to take similar values)
故特征选择为两个变量之间的距离函数(distance fuction),距离函数
1)自反性(Reflexivity):
2)对称性(Symmetry):
3)三角不等式(Triangle inequality):
满足条件 1, 2 称为半度量(semimetric)空间,均满足则称为度量(metric)空间。
特征函数取为
这里列举三种距离函数:
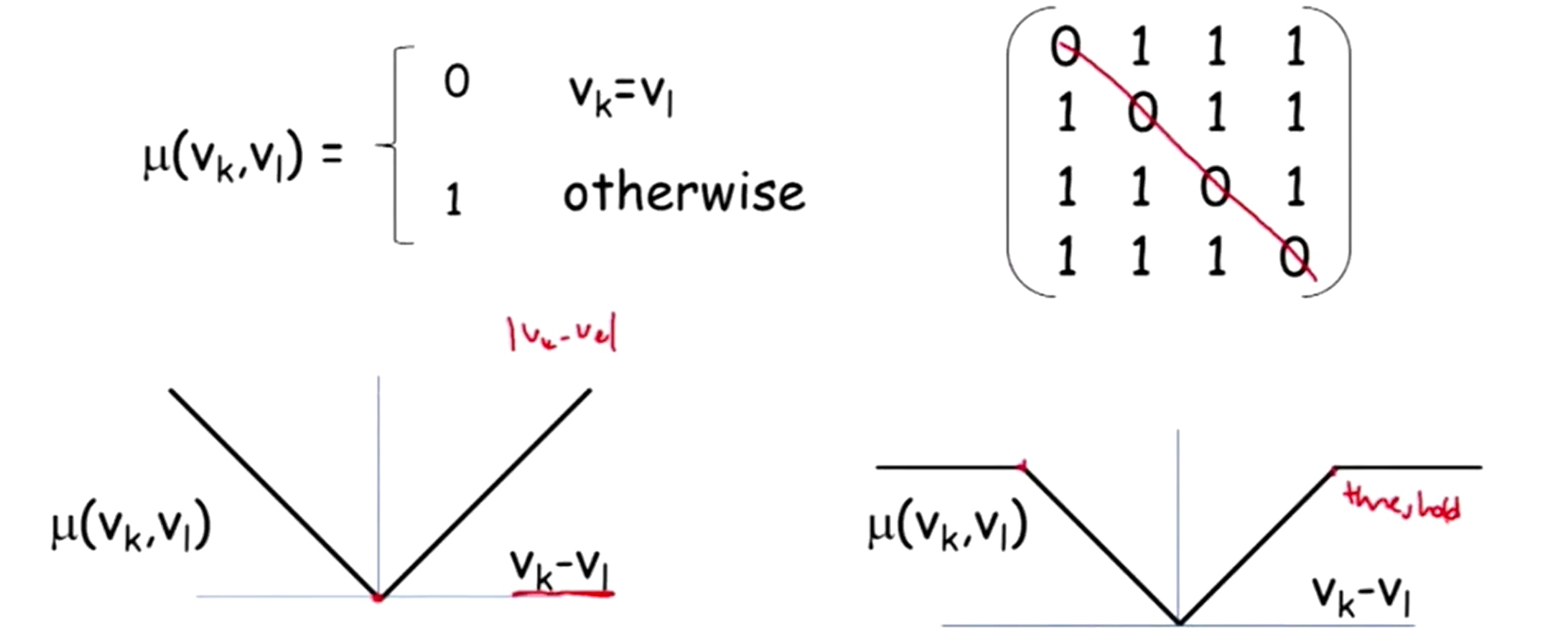
1)阶梯函数(step function): 到自身距离为 0,到其他节点的距离为 1;
2)线性函数(linear function): 距离定义为两个节点数值之差的绝对值;
3)截断范式(truncated linear penalty): 在 2)的基础上设限(threshold),当超过此上限距离函数的值为常数。
6.6 Metric MRFs 在计算机视觉的应用
马尔可夫网(MNs)的在计算机视觉领域(the context of of computer vision)的应用通常以成对马尔可夫随机场(pairwise MRFs)的形式出现。并在 pairwise MRFs 结构下选取距离函数作为特征函数,即为 Metric MRFs 。
这里举例 Metric MRFs 在三处应用中特征函数的选取(翻译版书 Page 111 中有相关介绍)。
注:由于计算代价昂贵,故常将图像先分成一些超级像素(superpixels),即一些连贯的小区域,然后对这些超级像素分类。属于一个超级像素内的所有像素被划分为同一类。
- 图像分割(Image Segementation)
目标:将图像中的像素按其对应场景分类(比如天空,草地,楼房);
分析:倾向于相邻超级像素被分为同一类,故当相邻两超级像素属于不同类时给予惩罚(penalty);
模型:变量对应于超级像素,在原图中每一对相邻的超级像素间存在一条边;
特征:以每一对有边相连的两变量为一个辖域,定义其上特征函数为 step function,权重刻画对相邻像素间应分为一类的偏好程度。
说明:1)这个特征是定义在像素值上,用来刻画图像中相邻超级像素之间的相似程度。实际中,特征函数还可以定义在像素的纹理,地点上来提取特征;
2)模型实际上在每个超级像素的分类标签上定义了一个条件随机场。
- 图像去噪(Image Denoising)
目标:还原赋值可能是噪声值的所有像素的真实值;
模型:同上;
特征:选择 truncated linear penalty。截断可以避免过度惩罚真实的不一致性比如物体边缘,以免图像过度光滑。
- 三维重建(Stereo Reconstruction)
目标:重建图像中每个像素的深度差异;
模型:同上;但变量取值不再是像素值,而是像素离散化程度所体现的深度维度 ( 离相机越近,像素更精细;反之离散化程度越高 );
特征:选择 truncated linear penalty。截断可以避免过度惩罚相邻像素之间的深度差异。
7 作为模板的共同特征
大部分 MRFs 中,相同的特征函数和权重系数被应用于许多不同的辖域上。这类比于贝叶斯网中的模板模型。这部分介绍 Shared Features in Log Linear Models。
7.1 应用举例
- 伊辛模型
每一对相邻节点上特征都选取为
- 自然语言处理
每一对词汇标签
每一对相邻标签(红边)组成的辖域上也定义相同的特征函数
- 图像分割:每一对相邻超级像素之间选取相同的距离函数,相同的权重。
7.2 选取与使用方法
Step 1:选定准备反复使用的一组(或一个)特征函数
Step 2:为每一个
Step 3:为每一个
Step 4:对每一个
7.3 总结
这里的 Shared features 类似于贝叶斯网的模板模型中的模板,它为 MNs 提供一个可以应用与多个 MNs 中的简单的模板。比如不同的图像,不同的句子。
可选取多个共同特征,每个特征都可应用于一组辖域
Scopes[fk] 。比如图中所有相邻的相邻像素,所有成对原子,句中所有的词。
注:实际应用中,常将同一辖域上提取出的多个特征函数做以聚类来实现降维。
至此本文详细介绍了 MNs 结构,模型和应用。回顾博文重点请点击这里返回开篇摘要。
- 王飞跃, 韩素青译. 概率图模型 - 原理与技术, 清华大学出版社, 2015: page 108. ↩
- 概率图模型笔记(6)——Markov Network Fundamentals. ↩
- 概率图模型笔记(6)——Markov Network Fundamentals. ↩