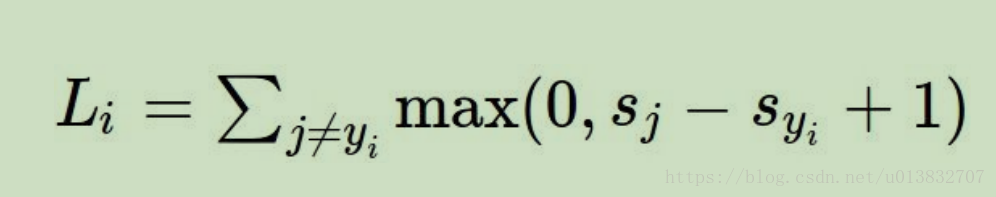版权声明:本文为博主原创文章,转载请联系作者 https://blog.csdn.net/u013832707/article/details/82862332
前言
本次作业需要完成:
- 实现SVM损失函数,并且是完全向量化的
- 实现相关的梯度计算,也是向量化的
- 使用数值梯度验证梯度是否正确
- 使用验证集来选择一组好的学习率以及正则化系数
- 使用SGD方法优化loss
- 可视化最终的权重
代码实现
使用for循环计算SVM的loss以及grad
其中W为权重矩阵,形状为(D,C);X为测试数据,形状为(N,D);y为X对应的标签值,形状为(N,);reg为正则化系数。
函数需要返回float型的loss以及W对应的梯度矩阵
svm的损失函数如下:
其中si是f(w,x)的计算结果S(N,)的第i项。表示样本属于第i类的概率,syi表示样本被分为正确类别的概率。
实现svm_loss_naive(W, X, y, reg)函数
def svm_loss_naive(W, X, y, reg):
"""
Structured SVM loss function, naive implementation (with loops).
Inputs have dimension D, there are C classes, and we operate on minibatches
of N examples.
Inputs:
- W: A numpy array of shape (D, C) containing weights.
- X: A numpy array of shape (N, D) containing a minibatch of data.
- y: A numpy array of shape (N,) containing training labels; y[i] = c means
that X[i] has label c, where 0 <= c < C.
- reg: (float) regularization strength
Returns a tuple of:
- loss as single float
- gradient with respect to weights W; an array of same shape as W
"""
dW = np.zeros(W.shape) # initialize the gradient as zero
# compute the loss and the gradient
num_classes = W.shape[1]
num_train = X.shape[0]
loss = 0.0
for i in range(num_train):
scores = X[i].dot(W) # X点乘W,获得S
correct_class_score = scores[y[i]] # 获得Syi
ds_w = np.repeat(X[i], num_classes).reshape(-1, num_classes) # 计算偏S偏W
dm_s = np.zeros(W.shape)
for j in range(num_classes):
if j == y[i]:
continue
margin = scores[j] - correct_class_score + 1 # note delta = 1
if margin > 0:
dm_s[:, j] = 1 #这两步计算偏margin偏S
dm_s[:, y[i]] -= 1
loss += margin
dW_i = ds_w * dm_s #计算偏margin偏w,单个输入
dW += dW_i # 求得总的梯度
# Right now the loss is a sum over all training examples, but we want it
# to be an average instead so we divide by num_train.
loss /= num_train
dW /= num_train
# Add regularization to the loss.
loss += reg * np.sum(W * W) # 加上正则化项
dW += W*2 # 加上正则化项的梯度
#############################################################################
# TODO: #
# Compute the gradient of the loss function and store it dW. #
# Rather that first computing the loss and then computing the derivative, #
# it may be simpler to compute the derivative at the same time that the #
# loss is being computed. As a result you may need to modify some of the #
# code above to compute the gradient. #
#############################################################################
return loss, dW
实现svm_loss_vectorized(W, X, y, reg)函数
这里实现的不是很好,需要进一步优化
def svm_loss_vectorized(W, X, y, reg):
"""
Structured SVM loss function, vectorized implementation.
Inputs and outputs are the same as svm_loss_naive.
"""
loss = 0.0
dW = np.zeros(W.shape) # initialize the gradient as zero
#############################################################################
# TODO: #
# Implement a vectorized version of the structured SVM loss, storing the #
# result in loss. #
#############################################################################
num_train = X.shape[0]
num_classes = W.shape[1]
scores = X.dot(W)
correct_class_scores = [ [1 - scores[i, y[i]]] * num_classes for i in range(num_train) ]
margins = scores + correct_class_scores
for i in range(num_train):
margins[i, y[i]] = 0
margins = np.maximum(margins, 0)
loss = np.sum(margins)
loss /= num_train
loss += reg * np.sum(W * W)
#############################################################################
# END OF YOUR CODE #
#############################################################################
#############################################################################
# TODO: #
# Implement a vectorized version of the gradient for the structured SVM #
# loss, storing the result in dW. #
# #
# Hint: Instead of computing the gradient from scratch, it may be easier #
# to reuse some of the intermediate values that you used to compute the #
# loss. #
#############################################################################
D = W.shape[0]
ds_w = np.repeat(X, num_classes).reshape(-1, num_classes)
dm_s = margins
dm_s[dm_s > 0] = 1
for i in range(num_train):
dm_s[i, y[i]] = -np.sum(dm_s[i])
dm_s = np.repeat(dm_s, D, 0)
dws = ds_w * dm_s
dws = np.vsplit(dws, num_train)
for i in range(num_train):
dW += dws[i]
dW /= num_train
dW += W*2
#############################################################################
# END OF YOUR CODE #
#############################################################################
return loss, dW
实现SGD
在实现了loss和gradient计算之后,实现SGD是很简单的事情,所以就不贴代码了