上一篇综述文章 里我们简单介绍了L2R三种方法的一个概要,接下来将对这三种方法做详细介绍。本篇文章介绍第一种L2R方法–pointwise方法
pointwise方法非常简单,考虑的是文档 (doc) 和查询 (query) 的绝对相关度,基于此,我们可以将排序问题转化为分类或者回归问题。我们以分类问题为例,一般来说,会根据相关度设置五个类别 {perfect ,excellent,good,fair,bad},对应数字 { 5,4,3,2,1 },然后根据查询和返回文档可以标注样本,得到这样的形式 (query, doc, label)。
因此我们准备的样本格式如下,其中
q
i
q_i
q i
i
i
i
x
j
(
i
)
x^{(i)}_{j}
x j ( i )
i
i
i
j
j
j
C
k
C_{k}
C k
Pointwise方法主要包括以下算法:Pranking (NIPS 2002), OAP-BPM (EMCL 2003), Ranking with Large Margin Principles (NIPS 2002), Constraint Ordinal Regression (ICML 2005)。
我们详细介绍一下Pranking算法,原文地址:https://pdfs.semanticscholar.org/906f/50f545890ca81231be7cec7c59555c679dba.pdf
对于给定的样本集合
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
.
.
.
,
(
x
t
,
y
t
)
}
\{(x^{1}, y^{1}),(x^{2}, y^{2}),...,(x^{t}, y^{t})\}
{ ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x t , y t ) }
x
i
∈
R
n
x^{i} \in \mathbb{R^{n}}
x i ∈ R n
y
∈
Y
y\in \mathcal{Y}
y ∈ Y
Y
=
{
1
,
2
,
3
,
.
.
.
,
k
}
\mathcal{Y}=\{1,2,3,...,k\}
Y = { 1 , 2 , 3 , . . . , k }
>
\gt
>
y
s
>
y
t
y^{s}\gt y^{t}
y s > y t
x
s
x^{s}
x s
x
t
x^{t}
x t
y
s
=
y
t
y^{s} = y^{t}
y s = y t
x
s
x^{s}
x s
x
t
x^{t}
x t
假设有一个排序规则
H
:
R
n
⟶
y
\mathcal{H}: \mathbb{R^n}\longrightarrow y
H : R n ⟶ y
w
w
w
b
1
≤
b
2
≤
.
.
.
≤
b
k
=
∞
b_1\leq b_2\leq ... \leq b_k=\infty
b 1 ≤ b 2 ≤ . . . ≤ b k = ∞
b
=
(
b
1
,
b
2
,
.
.
.
,
b
k
−
1
)
b=(b_1,b_2,...,b_{k-1})
b = ( b 1 , b 2 , . . . , b k − 1 )
w
⋅
x
<
b
r
w\cdot x \lt b_r
w ⋅ x < b r
b
r
b_r
b r
b
r
−
1
<
w
⋅
x
<
b
r
b_{r-1}\lt w\cdot x \lt b_{r}
b r − 1 < w ⋅ x < b r
r
r
r
w
w
w
b
b
b
x
x
x
H
(
x
)
=
min
r
∈
{
1
,
2
,
.
.
.
,
k
}
{
r
:
w
⋅
x
−
b
r
<
0
}
H(x)=\min_{r\in \{1,2,...,k\}}\{r:w\cdot x -b_r\lt 0\}
H ( x ) = r ∈ { 1 , 2 , . . . , k } min { r : w ⋅ x − b r < 0 }
具体算法如下:
Initialize: Set
w
1
=
0
,
b
1
1
,
.
.
.
,
b
k
−
1
1
=
0
,
b
k
1
=
+
∞
w^{1}=0,b_{1}^{1},...,b_{k-1}^{1}=0,b_{k}^{1}=+\infty
w 1 = 0 , b 1 1 , . . . , b k − 1 1 = 0 , b k 1 = + ∞ Loop: For
t
=
1
,
2
,
.
.
.
,
T
t=1,2,...,T
t = 1 , 2 , . . . , T
Get a new rank-value
x
t
∈
R
n
x^{t}\in \mathbb{R^n}
x t ∈ R n Predict
y
^
t
=
min
r
∈
{
1
,
2
,
.
.
.
,
k
}
{
r
:
w
⋅
x
−
b
r
<
0
}
\hat{y}^{t}=\min_{r\in \{1,2,...,k\}}\{r:w\cdot x -b_r\lt 0\}
y ^ t = min r ∈ { 1 , 2 , . . . , k } { r : w ⋅ x − b r < 0 } Get a new label
y
t
y^{t}
y t If
y
^
t
≠
y
t
\hat{y}^{t} \neq y^{t}
y ^ t ̸ = y t
w
t
w^{t}
w t (otherwise set
w
t
+
1
=
w
t
,
∀
r
:
b
r
t
+
1
=
b
r
t
w^{t+1}=w^{t}, \forall r:b_{r}^{t+1}=b_{r}^{t}
w t + 1 = w t , ∀ r : b r t + 1 = b r t
r
=
1
,
2
,
.
.
.
,
k
−
1
r=1,2,...,k-1
r = 1 , 2 , . . . , k − 1
y
t
<
r
y^{t}<r
y t < r
y
r
t
=
−
1
y_{r}^{t}=-1
y r t = − 1
y
r
t
=
1
y_{r}^{t}=1
y r t = 1
r
=
1
,
2
,
.
.
.
,
k
−
1
r=1,2,...,k-1
r = 1 , 2 , . . . , k − 1
(
w
t
⋅
x
t
−
b
r
t
)
−
y
r
t
≤
0
(w^{t}\cdot x^{t}-b_{r}^{t}) - y_{r}^{t}\le 0
( w t ⋅ x t − b r t ) − y r t ≤ 0
τ
r
t
=
y
r
t
\tau_{r}^{t}= y_{r}^{t}
τ r t = y r t
τ
r
t
=
1
\tau_{r}^{t}=1
τ r t = 1
w
t
+
1
⟵
w
t
+
(
∑
r
τ
r
t
)
x
t
w^{t+1}\longleftarrow w^{t}+(\sum_{r}\tau_{r}^{t})x^t
w t + 1 ⟵ w t + ( ∑ r τ r t ) x t
r
=
1
,
2
,
.
.
.
,
k
−
1
r=1,2,...,k-1
r = 1 , 2 , . . . , k − 1
b
r
t
+
1
⟵
b
r
t
−
τ
r
t
b_{r}^{t+1}\longleftarrow b_{r}^{t}-\tau_{r}^{t}
b r t + 1 ⟵ b r t − τ r t
Output:
H
(
x
)
=
min
r
∈
{
1
,
2
,
.
.
.
,
k
}
{
r
:
w
⋅
x
−
b
r
<
0
}
H(x)=\min_{r\in \{1,2,...,k\}}\{r:w\cdot x -b_r\lt 0\}
H ( x ) = min r ∈ { 1 , 2 , . . . , k } { r : w ⋅ x − b r < 0 }
我们希望预测的排序尽可能接近真实的排序值,因此学习算法的目标就是最小化真实排序值和预测排序值的差。经过
T
T
T
∑
t
=
1
T
∣
y
^
t
−
y
t
∣
\sum_{t=1}^{T}\lvert \hat y^{t}- y^{t} \rvert
∑ t = 1 T ∣ y ^ t − y t ∣
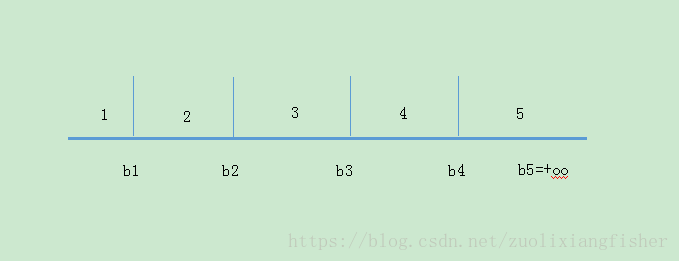
这个算法的更新规则灵感来源于对分类的感知算法,因此我们称为Prank (Perceptron Ranking),举个例子来说明这个算法的过程。假设rank集合
Y
\mathcal{Y}
Y
{
1
,
2
,
3
,
4
,
5
}
\{1,2,3,4,5\}
{ 1 , 2 , 3 , 4 , 5 }
b
5
=
∞
b_5= \infty
b 5 = ∞
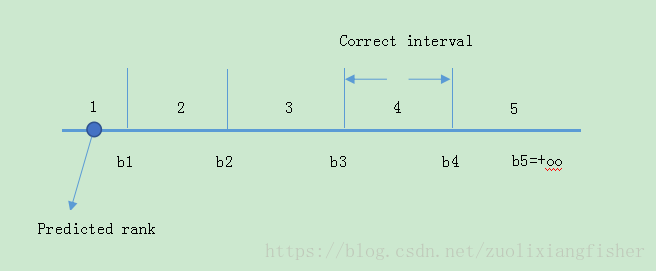
假设样本1的
y
y
y
w
T
⋅
x
w^{T}\cdot x
w T ⋅ x
b
3
b_3
b 3
b
4
b_4
b 4
y
^
\hat{y}
y ^
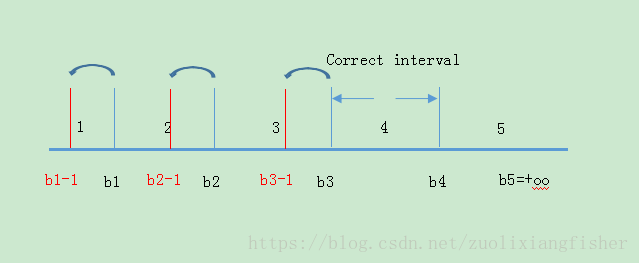
因此就产生了一个误差,为了修正这个误差,我们把
b
1
,
b
2
,
b
3
b_1,b_2,b_3
b 1 , b 2 , b 3
b
1
=
b
1
−
1
,
b
2
=
b
2
−
1
,
b
3
=
b
3
−
1
b_1=b_1-1,b_2=b_2-1,b_3=b_3-1
b 1 = b 1 − 1 , b 2 = b 2 − 1 , b 3 = b 3 − 1
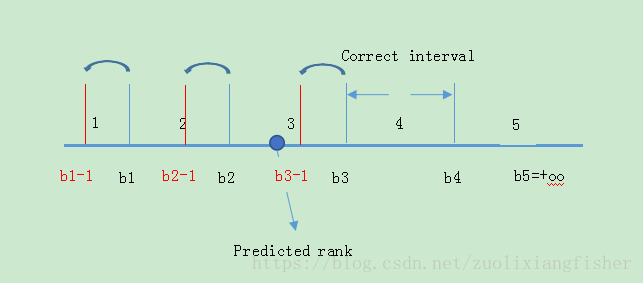
同时更新
w
=
w
+
(
1
+
1
+
1
)
x
w=w+(1+1+1)x
w = w + ( 1 + 1 + 1 ) x
w
⋅
x
w\cdot x
w ⋅ x
3
∣
∣
x
∣
∣
2
3|\lvert x\rvert|^{2}
3 ∣ ∣ x ∣ ∣ 2
以上基本就是prank算法的过程了,细心的同学可能会发现一个问题,就是一开始的时候我们假设
b
1
≤
b
2
≤
.
.
.
≤
b
k
=
∞
b_1\leq b_2\leq ... \leq b_k=\infty
b 1 ≤ b 2 ≤ . . . ≤ b k = ∞
b
i
b_i
b i
b
i
≥
b
j
b_i\geq b_j
b i ≥ b j
i
<
j
i<j
i < j
在证明保序引理之前,先回顾一下prank算法里提到的
τ
r
t
\tau_{r}^{t}
τ r t
(
w
t
⋅
x
t
−
b
r
t
)
−
y
r
t
≤
0
(w^{t}\cdot x^{t}-b_{r}^{t}) - y_{r}^{t}\le 0
( w t ⋅ x t − b r t ) − y r t ≤ 0
τ
r
t
=
y
r
t
\tau_{r}^{t}= y_{r}^{t}
τ r t = y r t
τ
r
t
=
1
\tau_{r}^{t}=1
τ r t = 1
⌊
π
⌋
\lfloor \pi\rfloor
⌊ π ⌋
π
\pi
π
⌊
π
⌋
\lfloor \pi\rfloor
⌊ π ⌋
τ
r
t
=
y
r
t
⌊
(
w
t
⋅
x
t
−
b
r
t
)
−
y
r
t
≤
0
⌋
\tau_{r}^{t}=y_{r}^{t} \lfloor(w^{t}\cdot x^{t}-b_{r}^{t}) - y_{r}^{t}\le 0\rfloor
τ r t = y r t ⌊ ( w t ⋅ x t − b r t ) − y r t ≤ 0 ⌋
b
r
t
∈
Z
,
b
r
1
=
0
b_{r}^{t}\in \mathbb{Z},b_{r}^{1}=0
b r t ∈ Z , b r 1 = 0
b
r
t
+
1
−
b
r
t
∈
{
−
1
,
0
,
+
1
}
b_{r}^{t+1}-b_{r}^{t}\in\{-1,0,+1\}
b r t + 1 − b r t ∈ { − 1 , 0 , + 1 }
w
t
,
b
t
w^{t},b^{t}
w t , b t
b
1
t
≤
b
2
t
≤
.
.
.
≤
b
k
−
1
t
b_{1}^{t}\leq b_{2}^{t}\leq ... \leq b_{k-1}^{t}
b 1 t ≤ b 2 t ≤ . . . ≤ b k − 1 t
(
x
t
,
y
t
)
(x^{t},y^{t})
( x t , y t )
t
t
t
w
t
+
1
,
b
t
+
1
w^{t+1},b^{t+1}
w t + 1 , b t + 1
b
1
t
+
1
≤
b
2
t
+
1
≤
.
.
.
≤
b
k
−
1
t
+
1
b_{1}^{t+1}\leq b_{2}^{t+1}\leq ... \leq b_{k-1}^{t+1}
b 1 t + 1 ≤ b 2 t + 1 ≤ . . . ≤ b k − 1 t + 1 证明:要证明prank算法对阈值保序,为方便起见我们沿用prank算法里对
y
r
t
y_{r}^{t}
y r t
r
<
y
t
r\lt y^{t}
r < y t
y
r
t
=
+
1
y_{r}^{t}=+1
y r t = + 1
r
≥
y
t
r\geq y^{t}
r ≥ y t
y
r
t
=
−
1
y_{r}^{t}=-1
y r t = − 1
r
r
r
b
r
+
1
t
+
1
≥
b
r
t
+
1
b_{r+1}^{t+1}\geq b_{r}^{t+1}
b r + 1 t + 1 ≥ b r t + 1
b
r
+
1
t
−
b
r
t
≥
y
r
+
1
t
⌊
(
w
t
⋅
x
t
−
b
r
+
1
t
)
−
y
r
+
1
t
≤
0
⌋
−
y
r
t
⌊
(
w
t
⋅
x
t
−
b
r
t
)
−
y
r
t
≤
0
⌋
(
∗
)
b_{r+1}^{t}-b_{r}^{t}\geq y_{r+1}^{t} \lfloor(w^{t}\cdot x^{t}-b_{r+1}^{t}) - y_{r+1}^{t}\le 0\rfloor-y_{r}^{t} \lfloor(w^{t}\cdot x^{t}-b_{r}^{t}) - y_{r}^{t}\le 0\rfloor (*)
b r + 1 t − b r t ≥ y r + 1 t ⌊ ( w t ⋅ x t − b r + 1 t ) − y r + 1 t ≤ 0 ⌋ − y r t ⌊ ( w t ⋅ x t − b r t ) − y r t ≤ 0 ⌋ ( ∗ )
r
r
r
t
t
t
t
+
1
t+1
t + 1
b
r
+
1
t
+
1
,
b
r
+
1
t
b_{r+1}^{t+1},b_{r+1}^{t}
b r + 1 t + 1 , b r + 1 t
t
t
t
b
r
+
1
t
−
b
r
t
>
0
b_{r+1}^{t}-b_{r}^{t}\gt 0
b r + 1 t − b r t > 0
b
r
+
1
t
,
b
r
t
∈
Z
b_{r+1}^{t},b_{r}^{t}\in \mathbb{Z}
b r + 1 t , b r t ∈ Z
b
r
+
1
t
−
b
r
t
≥
1
b_{r+1}^{t}-b_{r}^{t}\ge 1
b r + 1 t − b r t ≥ 1
b
r
+
1
t
+
1
−
b
r
t
+
1
≥
0
b_{r+1}^{t+1}-b_{r}^{t+1}\ge 0
b r + 1 t + 1 − b r t + 1 ≥ 0
b
r
+
1
t
−
b
r
t
=
0
b_{r+1}^{t}-b_{r}^{t}=0
b r + 1 t − b r t = 0
b
r
+
1
t
+
1
−
b
r
t
+
1
=
0
b_{r+1}^{t+1}-b_{r}^{t+1}=0
b r + 1 t + 1 − b r t + 1 = 0
b
r
+
1
t
+
1
−
b
r
t
+
1
≥
0
b_{r+1}^{t+1}-b_{r}^{t+1}\ge0
b r + 1 t + 1 − b r t + 1 ≥ 0
y
t
>
r
y^{t}\gt r
y t > r
y
r
t
=
1
y_{r}^{t}=1
y r t = 1
y
r
t
=
−
1
y_{r}^{t}=-1
y r t = − 1
y
r
+
1
t
≤
y
r
t
y_{r+1}^{t}\leq y_{r}^{t}
y r + 1 t ≤ y r t
y
r
+
1
t
≠
y
r
t
y_{r+1}^{t}\neq y_{r}^{t}
y r + 1 t ̸ = y r t
y
r
+
1
t
=
−
1
,
y
r
t
=
1
y_{r+1}^{t}=-1,y_{r}^{t}=1
y r + 1 t = − 1 , y r t = 1
(
∗
)
(*)
( ∗ )
(
∗
)
(*)
( ∗ )
(
∗
)
(*)
( ∗ )
y
r
+
1
t
=
y
r
t
y_{r+1}^{t}= y_{r}^{t}
y r + 1 t = y r t
(
∗
)
(*)
( ∗ )
b
r
+
1
t
=
b
r
t
b_{r+1}^{t}=b_{r}^{t}
b r + 1 t = b r t
(
∗
)
(*)
( ∗ )
(
∗
)
(*)
( ∗ )
b
r
+
1
t
≠
b
r
t
b_{r+1}^{t}\neq b_{r}^{t}
b r + 1 t ̸ = b r t
b
r
+
1
t
−
b
r
t
≥
1
b_{r+1}^{t}-b_{r}^{t}\geq 1
b r + 1 t − b r t ≥ 1
(
∗
)
(*)
( ∗ )
(
∗
)
(*)
( ∗ )
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
.
.
.
,
(
x
T
,
y
T
)
(x^{1},y^{1}),(x^{2},y^{2}),...,(x^{T},y^{T})
( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x T , y T )
x
t
∈
R
n
,
y
∈
{
1
,
2
,
.
.
,
k
}
x^{t} \in\mathbb{R^{n}},y\in\{1,2,..,k\}
x t ∈ R n , y ∈ { 1 , 2 , . . , k }
R
2
=
max
t
∣
∣
x
t
∣
∣
2
R^{2}=\max_{t}||x^{t}||^{2}
R 2 = max t ∣ ∣ x t ∣ ∣ 2
v
∗
=
(
w
∗
,
b
∗
)
,
b
1
∗
≤
b
2
∗
≤
.
.
.
≤
b
k
−
1
∗
v^{*}=(w^{*},b^{*}),b_{1}^{*}\leq b_{2}^{*}\leq ... \leq b_{k-1}^{*}
v ∗ = ( w ∗ , b ∗ ) , b 1 ∗ ≤ b 2 ∗ ≤ . . . ≤ b k − 1 ∗
γ
=
min
r
,
t
{
(
w
∗
⋅
x
t
−
b
r
∗
)
y
r
t
>
0
}
\gamma=\min_{r,t}\{(w^{*}\cdot x^{t}-b_{r}^{*})y_{r}^{t}\gt 0\}
γ = min r , t { ( w ∗ ⋅ x t − b r ∗ ) y r t > 0 }
∑
t
=
1
T
∣
y
^
t
−
y
t
∣
\sum_{t=1}^{T}|\hat y^{t}-y^{t}|
∑ t = 1 T ∣ y ^ t − y t ∣
(
k
−
1
)
(
R
2
+
1
)
/
γ
2
(k-1)(R^2+1)/{\gamma^{2}}
( k − 1 ) ( R 2 + 1 ) / γ 2 证明思路是利用数学归纳法和柯西-施瓦尔兹方法进行放缩来推导,具体过程不再赘述,可以直接参考论文证明过程,也可以后续留言交流。