[BZOJ2007][Noi2010]海拔（平面图最小割转对偶图最短路）

Address

https://www.lydsy.com/JudgeOnline/problem.php?id=2007

Solution

首先得 (cai) 出两个性质：
（1）存在一种最优方案使得任意点的海拔为 $0$ 或 $1$ 。
证明：如果一个点，周围点的海拔都是 $0$ 或 $1$ ，而该点的海拔为 $a$ ，那么这个点向上、下、左、右的边产生的代价可以写成 $xa+y(1-a)=(x-y)a+y$ 的形式，故最优情况下 $a$ 取 $0$ 或 $1$ 。
（2）海拔为 $0$ 的点构成一个连通块，海拔为 $1$ 的点构成一个连通块。
证明：如果一个点的海拔为 $0$ ，不在边界并且四周的海拔都为 $1$ ，那么显然这个点的海拔为 $1$ 时更优。其他情况同理。
于是我们得出：答案为左上角到右下角的最小割。
但图的规模较大，跑网络流会比较悬。
但这是一个网格图，也是一个平面图，故考虑最小割转最短路。
新建虚拟源汇 $S,T$ 。
下面 $right[i][j],down[i][j],left[i][j],up[i][j]$ 分别表示由 $(i,j)$ 向东、南、西、北的人流量。
对于每个 $1\le i\le n$ ：
（1）连边 $(S,(i,1),down[i][1])$ 。
（2）连边 $(S,(n,i),right[n+1][i])$ 。
（3）连边 $((1,i),T,right[1][i])$ 。
（4）连边 $((i,n),T,down[i][n+1])$ 。
对于每个 $1\le i,j\le n$ ：
（1）如果 $j>1$ 则连边 $((i,j),(i,j-1),up[i+1][j])$ 。
（2）如果 $j<n$ 则连边 $((i,j),(i,j+1),down[i][j+1])$ 。
（3）如果 $i>1$ 则连边 $((i,j),(i-1,j),right[i][j])$ 。
（4）如果 $i<n$ 则连边 $((i,j),(i+1,j),left[i+1][j+1])$ 。
画个图长这样：

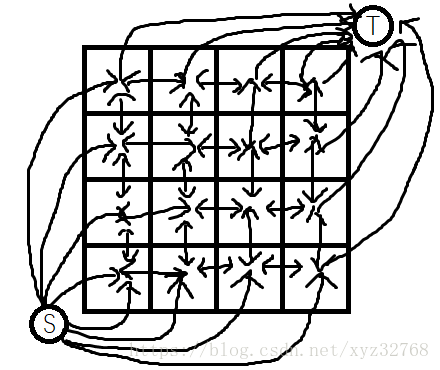
跑 Dijkstra 求 $S$ 到 $T$ 最短路即可。

Code

#include <cmath>
#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define For(i, a, b) for (i = a; i <= b; i++)
#define Edge(u) for (int e = adj[u], v = go[e]; e; e = nxt[e], v = go[e])
using namespace std;

inline int read()
{
    int res = 0; bool bo = 0; char c;
    while (((c = getchar()) < '0' || c > '9') && c != '-');
    if (c == '-') bo = 1; else res = c - 48;
    while ((c = getchar()) >= '0' && c <= '9')
        res = (res << 3) + (res << 1) + (c - 48);
    return bo ? ~res + 1 : res;
}

typedef long long ll;
const int N = 505, M = 25e4 + 16, L = 1e6 + 2005;
const ll INF = 1ll << 60;
int n, ri[N][N], dw[N][N], le[N][N], up[N][N], S, T, ecnt, nxt[L],
adj[M], go[L], val[L];
ll dis[M];
bool vis[M];

void add_edge(int u, int v, int w)
{
    nxt[++ecnt] = adj[u]; adj[u] = ecnt; go[ecnt] = v; val[ecnt] = w;
}

struct node
{
    int u; ll dis;
    friend inline bool operator < (node a, node b)
    {
        return a.dis > b.dis;
    }
};

priority_queue<node> pq;

int which(int i, int j)
{
    return (i - 1) * n + j;
}

int main()
{
    int i, j;
    n = read();
    For (i, 1, n + 1) For (j, 1, n)
        ri[i][j] = read();
    For (i, 1, n) For (j, 1, n + 1)
        dw[i][j] = read();
    For (i, 1, n + 1) For (j, 2, n + 1)
        le[i][j] = read();
    For (i, 2, n + 1) For (j, 1, n + 1)
        up[i][j] = read();
    S = n * n + 1; T = S + 1;
    For (i, 1, n) add_edge(S, which(i, 1), dw[i][1]);
    For (i, 1, n) add_edge(S, which(n, i), ri[n + 1][i]);
    For (i, 1, n) add_edge(which(1, i), T, ri[1][i]);
    For (i, 1, n) add_edge(which(i, n), T, dw[i][n + 1]);
    For (i, 1, n) For (j, 1, n)
    {
        if (j > 1) add_edge(which(i, j), which(i, j - 1), up[i + 1][j]);
        if (j < n) add_edge(which(i, j), which(i, j + 1), dw[i][j + 1]);
        if (i > 1) add_edge(which(i, j), which(i - 1, j), ri[i][j]);
        if (i < n) add_edge(which(i, j), which(i + 1, j), le[i + 1][j + 1]);
    }
    For (i, 1, T) dis[i] = INF;
    dis[S] = 0;
    pq.push((node) {S, 0});
    while (!pq.empty())
    {
        node x = pq.top(); pq.pop();
        if (vis[x.u]) continue;
        int u = x.u; vis[u] = 1;
        Edge(u) if (dis[u] + val[e] < dis[v])
            dis[v] = dis[u] + val[e], pq.push((node) {v, dis[v]});
    }
    cout << dis[T] << endl;
    return 0;
}