什么是约瑟夫环问题?
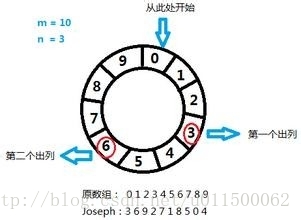
约瑟夫问题是个著名的问题:N个人围成一圈,第一个人从1开始报数,报M的将被杀掉,下一个人接着从1开始报。如此反复,最后剩下一个,求最后的胜利者。
例如只有三个人,把他们叫做A、B、C,他们围成一圈,从A开始报数,假设报2的人被杀掉。
- 首先A开始报数,他报1。侥幸逃过一劫。
- 然后轮到B报数,他报2。非常惨,他被杀了
- C接着从1开始报数
- 接着轮到A报数,他报2。也被杀死了。
- 最终胜利者是C
解决约瑟夫环问题,我们首先来分析一下!
刚学数据结构的时候,我们可能用链表的方法去模拟这个过程,N个人看作是N个链表节点,节点1指向节点2,节点2指向节点3,……,节点N-1指向节点N,节点N指向节点1,这样就形成了一个环。然后从节点1开始1、2、3……往下报数,每报到M,就把那个节点从环上删除。下一个节点接着从1开始报数。最终链表仅剩一个节点。它就是最终的胜利者。
缺点:
要模拟整个游戏过程,时间复杂度高达O(nm),当n,m非常大(例如上百万,上千万)的时候,几乎是没有办法在短时间内出结果的。
约瑟夫环是一个经典的数学问题,我们不难发现这样的依次报数,似乎有规律可循。为了方便导出递推式,我们重新定义一下题目。
问题: N个人编号为1,2,……,N,依次报数,每报到M时,杀掉那个人,求最后胜利者的编号。
这边我们先把结论抛出了。之后带领大家一步一步的理解这个公式是什么来的。
递推公式:
f(N,M)=(f(N−1,M)+M)%N f(N,M)=(f(N−1,M)+M)%N
- f(N,M) f(N,M) 表示,N个人报数,每报到M时杀掉那个人,最终胜利者的编号
- f(N−1,M) f(N−1,M) 表示,N-1个人报数,每报到M时杀掉那个人,最终胜利者的编号
下面我们不用字母表示每一个人,而用数字。
1、2、3、4、5、6、7、8、9、10、11 1、2、3、4、5、6、7、8、9、10、11
表示11个人,他们先排成一排,假设每报到3的人被杀掉。
- 刚开始时,头一个人编号是1,从他开始报数,第一轮被杀掉的是编号3的人。
- 编号4的人从1开始重新报数,这时候我们可以认为编号4这个人是队伍的头。第二轮被杀掉的是编号6的人。
- 编号7的人开始重新报数,这时候我们可以认为编号7这个人是队伍的头。第三轮被杀掉的是编号9的人。
- ……
- 第九轮时,编号2的人开始重新报数,这时候我们可以认为编号2这个人是队伍的头。这轮被杀掉的是编号8的人。
- 下一个人还是编号为2的人,他从1开始报数,不幸的是他在这轮被杀掉了。
- 最后的胜利者是编号为7的人。
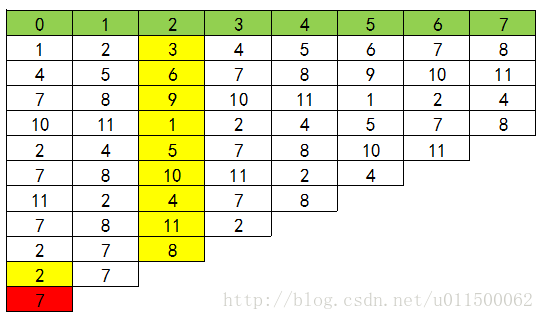
下图表示这一过程(先忽视绿色的一行)
现在再来看我们递推公式是怎么得到的!
将上面表格的每一行看成数组,这个公式描述的是:幸存者在这一轮的下标位置
- f(1,3) f(1,3) :只有1个人了,那个人就是获胜者,他的下标位置是0
- f(2,3)=(f(1,3)+3)%2=3%2=1 f(2,3)=(f(1,3)+3)%2=3%2=1 :在有2个人的时候,胜利者的下标位置为1
- f(3,3)=(f(2,3)+3)%3=4%3=1 f(3,3)=(f(2,3)+3)%3=4%3=1 :在有3个人的时候,胜利者的下标位置为1
- f(4,3)=(f(3,3)+3)%4=4%4=0 f(4,3)=(f(3,3)+3)%4=4%4=0 :在有4个人的时候,胜利者的下标位置为0
- ……
- f(11,3)=6 f(11,3)=6
很神奇吧!现在你还怀疑这个公式的正确性吗?上面这个例子验证了这个递推公式的确可以计算出胜利者的下标,下面将讲解怎么推导这个公式。
问题1:假设我们已经知道11个人时,胜利者的下标位置为6。那下一轮10个人时,胜利者的下标位置为多少?
答:其实吧,第一轮删掉编号为3的人后,之后的人都往前面移动了3位,胜利这也往前移动了3位,所以他的下标位置由6变成3。
问题2:假设我们已经知道10个人时,胜利者的下标位置为3。那下一轮11个人时,胜利者的下标位置为多少?
答:这可以看错是上一个问题的逆过程,大家都往后移动3位,所以f(11,3)=f(10,3)+3 f(11,3)=f(10,3)+3 。不过有可能数组会越界,所以最后模上当前人数的个数,f(11,3)=(f(10,3)+3)%11 f(11,3)=(f(10,3)+3)%11
问题3:现在改为人数改为N,报到M时,把那个人杀掉,那么数组是怎么移动的?
答:每杀掉一个人,下一个人成为头,相当于把数组向前移动M位。若已知N-1个人时,胜利者的下标位置位f(N−1,M) f(N−1,M) ,则N个人的时候,就是往后移动M为,(因为有可能数组越界,超过的部分会被接到头上,所以还要模N),既f(N,M)=(f(N−1,M)+M)%n f(N,M)=(f(N−1,M)+M)%n
注:理解这个递推式的核心在于关注胜利者的下标位置是怎么变的。每杀掉一个人,其实就是把这个数组向前移动了M位。然后逆过来,就可以得到这个递推式。
因为求出的结果是数组中的下标,最终的编号还要加1。
剑指offer题目:每年六一儿童节,牛客都会准备一些小礼物去看望孤儿院的小朋友,今年亦是如此。HF作为牛客的资深元老,自然也准备了一些小游戏。其中,有个游戏是这样的:首先,让小朋友们围成一个大圈。然后,他随机指定一个数m,让编号为0的小朋友开始报数。每次喊到m-1的那个小朋友要出列唱首歌,然后可以在礼品箱中任意的挑选礼物,并且不再回到圈中,从他的下一个小朋友开始,继续0...m-1报数....这样下去....直到剩下最后一个小朋友,可以不用表演,并且拿到牛客名贵的“名侦探柯南”典藏版(名额有限哦!!^_^)。请你试着想下,哪个小朋友会得到这份礼品呢? (注:小朋友的编号是从0到n-1)
拿到这一题,对比上面的两种思路:
1)使用数组模仿一个环。
2)使用公式递归求解。
首先看第一种思路:
class Solution {
public:
int LastRemaining_Solution(unsigned int n, unsigned int m)
{
/*
每轮被select的数被设置成-1;
超出数组范围的,回到数组起点,模仿一个环;
每次再次走到之前select的数的时候,就continue;
*/
//if(n<1||m<1) return -1;
int* array = new int[n];
int i = -1, step = 0, count = n;
while(count>0){
i++;
if(i>=n) i = 0;//模仿一个环
if(array[i]==-1) continue;//每次再走到之前select的数时,就continue;
step++;
if(step == m){
array[i] = -1; //每轮被select的数被设置成-1;
step = 0;
count--;
}
}
return i; //此题小朋友的编号是从0到n-1
}
};
再看第二种思路:
class Solution {
public:
int LastRemaining_Solution(unsigned int n, unsigned int m)
{
if(n==0)
return -1;
if(n==1)
return 0;
else
return (LastRemaining_Solution(n-1,m)+m)%n;
}
};