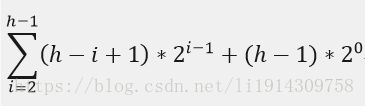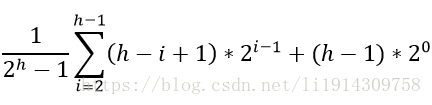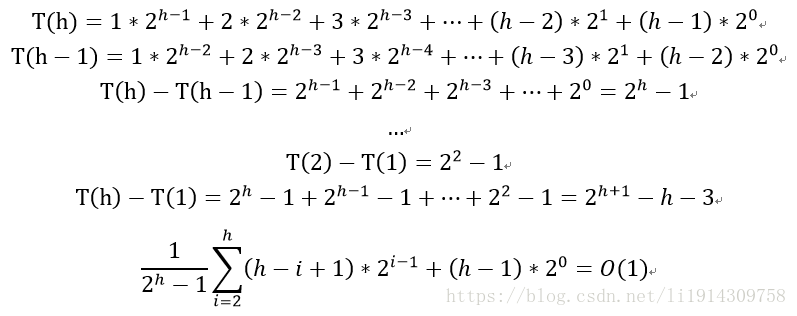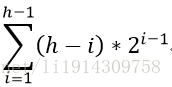大小堆介绍部分转载自:二叉堆之图文解析
复杂度分析和代码是自己写的~
堆和二叉堆的介绍
堆的定义
堆(heap),这里所说的堆是数据结构中的堆,而不是内存模型中的堆。堆通常是一个可以被看做一棵树,它满足下列性质:
[性质一] 堆中任意节点的值总是不大于(不小于)其子节点的值;
[性质二] 堆总是一棵完全树。
将任意节点不大于其子节点的堆叫做最小堆或小根堆,而将任意节点不小于其子节点的堆叫做最大堆或大根堆。常见的堆有二叉堆、左倾堆、斜堆、二项堆、斐波那契堆等等。
二叉堆的定义
二叉堆是完全二元树或者是近似完全二元树,它分为两种:最大堆和最小堆。
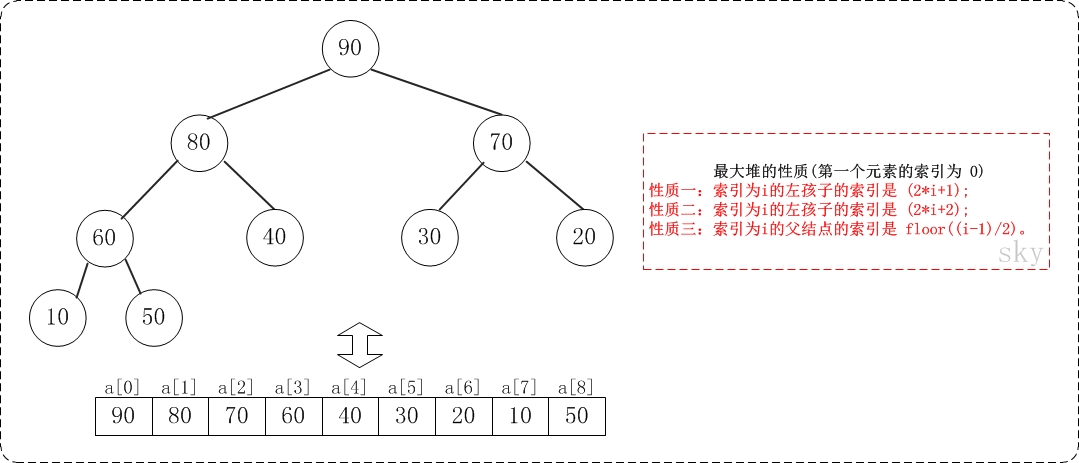
最大堆:父结点的键值总是大于或等于任何一个子节点的键值;最小堆:父结点的键值总是小于或等于任何一个子节点的键值。示意图如下:
二叉堆一般都通过"数组"来实现。数组实现的二叉堆,父节点和子节点的位置存在一定的关系。有时候,我们将"二叉堆的第一个元素"放在数组索引0的位置,有时候放在1的位置。当然,它们的本质一样(都是二叉堆),只是实现上稍微有一丁点区别。
假设"第一个元素"在数组中的索引为 0 的话,则父节点和子节点的位置关系如下:
(01) 索引为i的左孩子的索引是 (2*i+1);
(02) 索引为i的右孩子的索引是 (2*i+2);(图中性质二有错,应该改为右孩子)
(03) 索引为i的父结点的索引是 floor((i-1)/2);

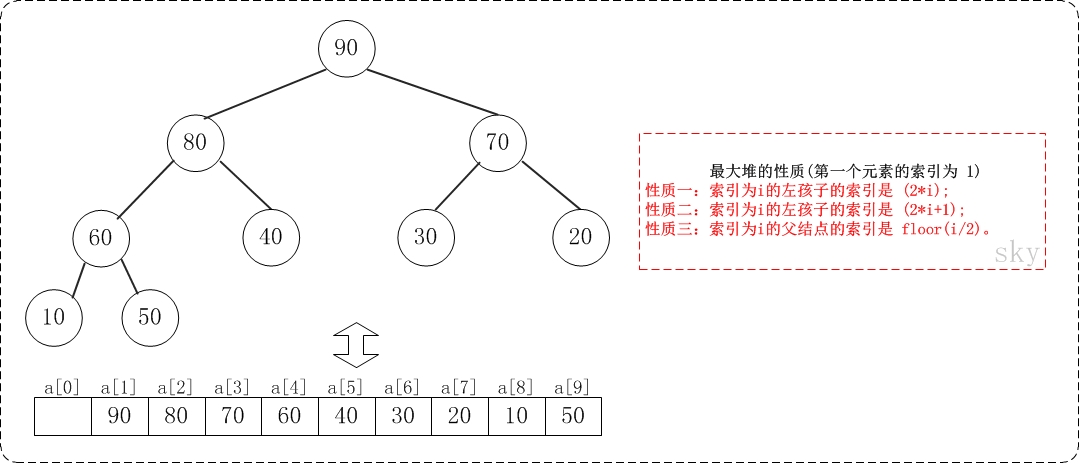
假设"第一个元素"在数组中的索引为 1 的话,则父节点和子节点的位置关系如下:
(01) 索引为i的左孩子的索引是 (2*i);
(02) 索引为i的右孩子的索引是 (2*i+1);(图中性质二有错,应该改为右孩子)
(03) 索引为i的父结点的索引是 floor(i/2);
注意:本文二叉堆的实现统统都是采用"二叉堆第一个元素在数组索引为0"的方式!
二叉堆的图文解析
在前面,我们已经了解到:"最大堆"和"最小堆"是对称关系。这也意味着,了解其中之一即可。本节的图文解析是以"最大堆"来进行介绍的。
二叉堆的核心是"添加节点"和"删除节点",理解这两个算法,二叉堆也就基本掌握了。下面对它们进行介绍。
1. 添加
假设在最大堆[90,80,70,60,40,30,20,10,50]种添加85,需要执行的步骤如下:
如上图所示,当向最大堆中添加数据时:先将数据加入到最大堆的最后,然后尽可能把这个元素往上挪,直到挪不动为止!
将85添加到[90,80,70,60,40,30,20,10,50]中后,最大堆变成了[90,85,70,60,80,30,20,10,50,40]。
void insertMaxHeap(int a, vector<int>& heap) {
heap.push_back(a);
int insertPos=heap.size()-1, parentPos=(insertPos-1)/2;
while(parentPos>=0 && heap[parentPos]<heap[insertPos]) {
swap(heap, insertPos, parentPos);
insertPos=parentPos;
parentPos=(insertPos-1)/2;
}
}
void insertMinHeap(int a, vector<int>& heap) {
heap.push_back(a);
int insertPos=heap.size()-1, parentPos=(insertPos-1)/2;
while(parentPos>=0 && heap[parentPos]>heap[insertPos]) {
swap(heap, parentPos, insertPos);
insertPos=parentPos;
parentPos=(insertPos-1)/2;
}
}2. 删除
假设从最大堆[90,85,70,60,80,30,20,10,50,40]中删除90,需要执行的步骤如下:
从[90,85,70,60,80,30,20,10,50,40]删除90之后,最大堆变成了[85,80,70,60,40,30,20,10,50]。
如上图所示,当从最大堆中删除数据时:先删除该数据,然后用最大堆中最后一个的元素插入这个空位;接着,把这个“空位”尽量往上挪,直到剩余的数据变成一个最大堆。
注意:考虑从最大堆[90,85,70,60,80,30,20,10,50,40]中删除60,执行的步骤不能单纯的用它的子节点来替换;而必须考虑到"替换后的树仍然要是最大堆"!
void deleteMaxHeap(int a, vector<int>& heap) {
auto it=find(heap.begin(), heap.end(), a);
if(it==heap.end()) {
cout << "The value is not stored in the max-heap." << endl;
return;
}
*it=heap[heap.size()-1];
heap.erase(heap.end()-1);
int deletePos=it-heap.begin(), leftChildPos=2*deletePos+1, rightChildPos=2*deletePos+2;
int maxPos=deletePos;
while(deletePos<(int)heap.size()) {
maxPos=deletePos;
if(rightChildPos<(int)heap.size() && heap[rightChildPos]>heap[maxPos]) {
maxPos=rightChildPos;
}
if(leftChildPos<(int)heap.size() && heap[leftChildPos]>heap[maxPos]) {
maxPos=leftChildPos;
}
if(maxPos!=deletePos) {
swap(heap, deletePos, maxPos);
deletePos=maxPos;
leftChildPos=2*deletePos+1;
rightChildPos=2*deletePos+2;
}
else {
break;
}
}
}
void deleteMinHeap(int a, vector<int>& heap) {
auto it=find(heap.begin(), heap.end(), a);
if(it==heap.end()) {
cout << "The value is not stored in the min-heap." << endl;
return;
}
*it=heap[heap.size()-1];
heap.erase(heap.end()-1);
int deletePos=it-heap.begin(), leftChildPos=2*deletePos+1, rightChildPos=leftChildPos+1;
int minPos=deletePos;
while(deletePos<(int)heap.size()) {
minPos=deletePos;
if(rightChildPos<(int)heap.size() && heap[rightChildPos]<heap[minPos]) {
minPos=rightChildPos;
}
if(leftChildPos<(int)heap.size() && heap[leftChildPos]<heap[minPos]) {
minPos=leftChildPos;
}
if(minPos!=deletePos) {
swap(heap, deletePos, minPos);
deletePos=minPos;
leftChildPos=deletePos*2+1;
rightChildPos=leftChildPos+1;
}
else {
break;
}
}
}
void swap(vector<int>& heap, int p1, int p2) {
int t=heap[p1];
heap[p1]=heap[p2];
heap[p2]=t;
}
二叉堆的插入、删除以及构造时间复杂度分析(最大堆为例)
二叉堆的插入
最好情况下,需要插入的节点只需要一次比较,比它的父节点小即可。因此时间复杂度为O(1)
最差情况下,需要插入的节点要一直从倒数第二层比较到第一层的根节点,共比较(h-1)次,h为高度。由于高为h的完全二叉树的节点数最多为2^h-1,所以有h=log(n+1),n为节点数。故最差情况下插入的时间复杂度为O(logn)
平均情况下,需要插入的节点最终位于二叉堆的各个位置的概率均为1/(2^h-1),而第i层的节点个数为2^(i-1),如果该插入的节点最终位于第i层,则完成该插入操作需要比较(i-1)次。所以平均情况下的比较操作共:
故平均情况下,插入的时间复杂度为
求解得:
因此平均情况下插入的复杂度为O(1)
二叉堆的删除
最好情况下,二叉堆的删除只需要直接将被删除节点与数组最后的节点交换一次,并和子节点比较一次即可,复杂度为O(1)
最坏情况下,二叉堆的删除在交换后,需要将替换的节点与他的两个子节点进行比较,比较次数最多为(h-1)次,复杂度为O(logn)
二叉堆的构造
二叉堆的构造方法有两种,分别采用的是插入和删除的思想。
采用二叉堆插入思想进行二叉堆构造
可以想象刚开始是一个空堆,不停地将将元素插入这个堆。总共n个元素,每次插入时间复杂度为O(logn),因此总的复杂度为O(nlogn)。
/* Apply insertion to construct heap.
* Complexity is O(nlogn).
*/
void constructMaxHeap(const vector<int>& nums, vector<int>& heap) {
for(const auto i:nums) {
heap.push_back(i);
int insertPos=heap.size()-1, parentPos=(insertPos-1)/2;
while(parentPos>=0 && heap[parentPos]<heap[insertPos]) {
swap(heap, parentPos, insertPos);
insertPos=parentPos;
parentPos=(insertPos-1)/2;
}
}
}
void constructMinHeap(const vector<int>& nums, vector<int>& heap) {
for(auto num:nums) {
heap.push_back(num);
int insertPos=heap.size()-1, parentPos=(insertPos-1)/2;
while(parentPos>=0 && heap[parentPos]>heap[insertPos]) {
swap(heap, parentPos, insertPos);
insertPos=parentPos;
parentPos=(insertPos-1)/2;
}
}
}采用二叉堆删除的思想构造二叉堆
可以直接将输入的数组看成一个二叉堆,只不过这个二叉堆现在不是最大堆,我们需要对它进行调整。调整直接从倒数第二层靠右边第一个有孩子的节点开始(倒数第一层都是叶子节点,不需要调整)一直到根节点止。调整的过程就是不断将待调整的节点与它的孩子比较,直到该节点的值比它的孩子都大或者该节点成为叶子节点。当需要调整的节点位于第i层,则该层共有2^(i-1)个节点,每次调整需要比较(h-i)次,因此总共的比较次数为
与之前的分析类似,此时构造二叉堆的复杂度为2^k -k -1=O(n)
void constructMaxHeap(vector<int> &num) {
int pos=(num.size()-2)/2;
for(; pos>=0; --pos) {
maxifyHeap(num, pos);
}
}
void maxifyHeap(vector<int> &num, int pos) {
int maxPos=pos, leftChildPos=2*pos+1, rightChildPos=leftChildPos+1;
while(pos<num.size()) {
maxPos=pos;
if(leftChildPos<num.size() && num[leftChildPos]>num[maxPos]) {
maxPos=leftChildPos;
}
if(rightChildPos<num.size() && num[rightChildPos]>num[maxPos]) {
maxPos=rightChildPos;
}
if(maxPos!=pos) {
swap(num, maxPos, pos);
pos=maxPos;
leftChildPos=2*pos+1;
rightChildPos=leftChildPos+1;
}
else {
break;
}
}
}
void constructMinHeap(vector<int> &num) {
int pos=(num.size()-2)/2;
for(; pos>=0; --pos) {
minifyHeap(num, pos);
}
}
void minifyHeap(vector<int> &num, int pos) {
int minPos=pos, leftChildPos=2*pos+1, rightChildPos=2*pos+2;
while(pos<num.size()) {
minPos=pos;
if(leftChildPos<num.size() && num[leftChildPos]<num[minPos]) {
minPos=leftChildPos;
}
if(rightChildPos<num.size() && num[rightChildPos]<num[minPos]) {
minPos=rightChildPos;
}
if(minPos!=pos) {
swap(num, pos, minPos);
pos=minPos;
leftChildPos=2*pos+1;
rightChildPos=leftChildPos+1;
}
else {
break;
}
}
}