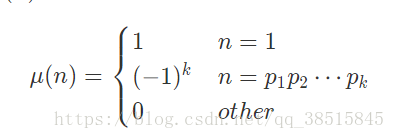题意是给出莫比乌斯函数和n、m,求。
今天看了很久tls的博客,才算对积性函数和杜教筛稍微有了一点了解。链接:点击此处查看原文。
首先,这道题的n和m的范围都很大,所以线性的做法肯定是解决不了问题的。其次,杜教筛有一道求莫比乌斯函数前缀和的模板题(可惜此前我并没有学过杜教筛...据说预处理个值的前缀和的情况下,可以在O(
)的时间复杂度下求出到n的前缀和...),因此
很容易就会往杜教筛上联想,所以需要想办法将问题转化为求莫比乌斯函数的前缀和。
首先,当n含有平方因子时,答案为0;
否则,因为莫比乌斯函数为积性函数,若i与n的任意一个因子d互质,则有,则可得
,后面加上的那部分代表d的所有在m以内的倍数乘以n/d的莫比乌斯函数的和,
。为什么要加上它呢?因为当i与d不互质时,i和n/d可能互质,也就是说可能出现
但是
的情况,如果只含有前面那部分的话相当于多减掉了这部分的
,因此需要加上这部分。当然,加上的这部分中肯定也包括了两者都为0的情况,但是都为0对结果没有影响,算上也没关系,方便计算。
由上面的式子可以看出,可以通过递归计算,当出现m=0的情况时,返回0;当出现n=1的情况时,返回前缀和(通过杜教筛计算)。
代码如下:
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define db double
#define ldb long double
#define m_p make_pair
#define p_b push_back
#define fbo friend bool operator <
const int N = 1000010;
const int mod=1e9+7;
bool notprime[N];
ll prime[N/10],cnt,mu[N];
vector<ll> fac;
inline bool Prime(ll x){
notprime[1]=mu[1]=1;
For(i,2,N-1){
if(!notprime[i]) prime[cnt++]=i,mu[i]=-1;
for(int j=0;j<cnt&&prime[j]*i<N;j++){
notprime[prime[j]*i]=true;
if(i%prime[j]==0) break;
mu[prime[j]*i]=-mu[i];
}
}
For(i,2,N-1) mu[i]+=mu[i-1];
for(int i=0;i<cnt&&prime[i]<=x;i++){
if(x%prime[i]==0){
fac.p_b(prime[i]);
x/=prime[i];
if(x%prime[i]==0) return false;
}
}
if(x>1) fac.p_b(x);
return true;
}
unordered_map<ll,ll> S;
inline ll Sum(ll x){
if (x<N) return mu[x];
if (S.find(x)!=S.end()) return S[x];
ll tem=1;
ll l,r;
for (l=2;l*l<=x;l++) tem-=Sum(x/l);
for (ll t=x/l;l<=x;l=r+1,t--){
r=x/t;
tem-=(r-l+1)*Sum(t);
}
return S[x]=tem;
}
inline ll cal(ll x,ll y){
if(x==0) return 0;
if(y==1) return Sum(x);
For(i,0,(int)fac.size()-1){
if(y%fac[i]==0){
return cal(x/fac[i],y)-cal(x,y/fac[i]);
}
}
}
ll n,m;
int main(){
// freopen("1.txt","r",stdin);
cin>>m>>n;
if(Prime(n)){
printf("%lld\n",cal(m,n));
}
else printf("0\n");
return 0;
}