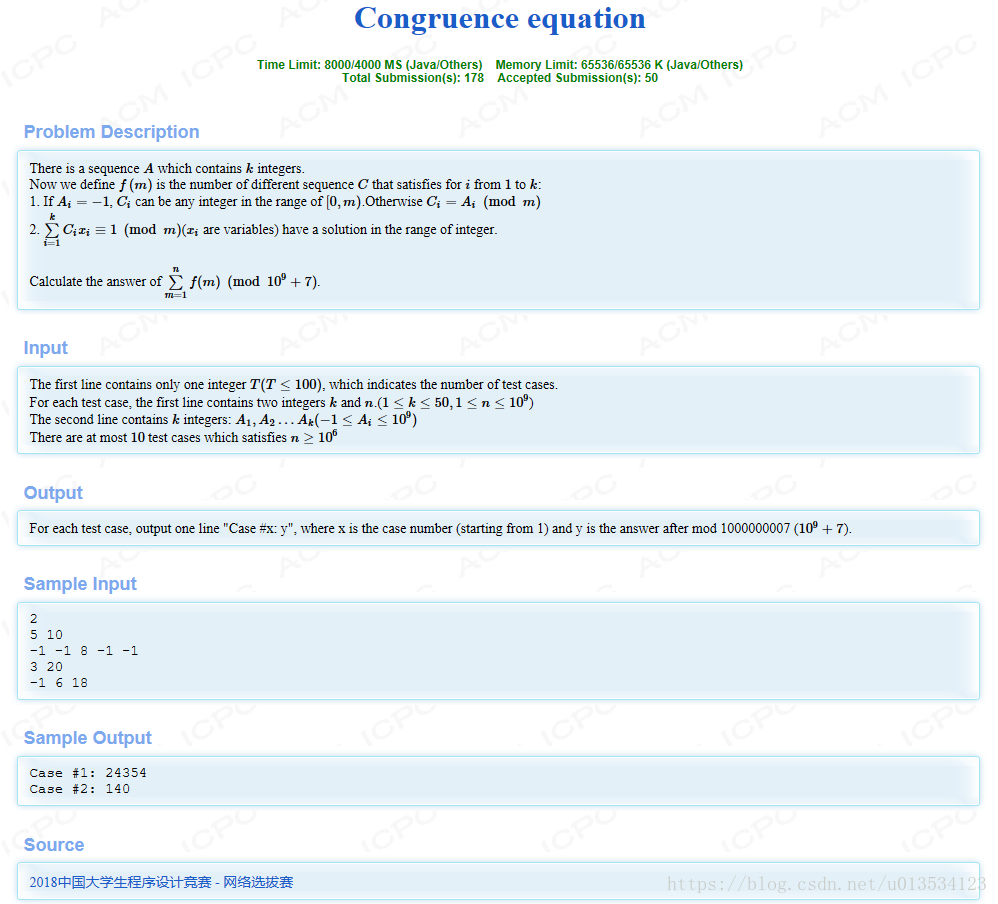
HDU 6439 2018CCPC网络赛 Congruence equationI（杜教筛 + 莫比乌斯反演 + 伯努利数）

大致题意：给你一个长度为k的序列a。对于序列c，当 $\large a_i\neq-1$ 时， $\large c_i=a_i\ mod\ m$ ；当 $\large a_i=-1$ 时， $\large c_i$ 取[0,m)中任意一个数字。令 $\large f(m)$ 表示满足 $\sum c_ix_i\equiv1(mod\ m)$ 的序列c的方案数。现在让你求 $\sum_{m=1}^{n}f(m)$ 。

首先，根据裴蜀定理，满足 $\sum c_ix_i\equiv1(mod\ m)$ 的条件是 $\large gcd(c_1,c_2,...,c_k,m)=1$ ，那么我们不妨分为两种情况处理。对于 $\large a_i\neq-1$ 的数字，假设他们的gcd为g，那么剩下的数字与g的gcd就要是1。设 $\large a_i=-1$ 的项有k个，加上这个m，设这k+1个数字的gcd为d，那么gcd(d,g)要等于1。由于这k+1个数字里面有一个定值m，所以这个d一定是m的因子。我们令f(d)表示这k+1个数字的gcd为d的方案数。那么开始第一次莫比乌斯反演，有：

$\large \begin{align*}F(d)&=\sum_{d|i,i|m}f(i)=(\frac{m}{d})^k \\ f(d)&=\sum_{d|i,i|m}\mu(\frac{i}{d})F(i)\\&= \sum_{d|i,i|m}\mu(\frac{i}{d})(\frac{m}{i})^k\\&=\sum_{i|\frac{m}{d}}\mu(i)(\frac{m}{id})^k\end{align*}$

令 $h(d)=\sum_{i|d}\mu(i)(\frac{m}{id})^k$ ，那么最后的答案就是:

$\large \begin{align*}ans&=\sum_{m=1}^{n}\sum_{d|m}h(d)[gcd(d,g)==1]\\ &=\sum_{d=1}^{n}h(d)\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}[gcd(i,g)==1]\end{align*}$

令 $g(m,d)=\sum_{i=1}^{m}[gcd(i,g)==d]$ ，于是我们开始第二次莫比乌斯反演：

$\large \begin{align*}G(m,d)&=\sum_{d|i,i|g}^{m}f(i)=\lfloor\frac{m}{d}\rfloor \\ g(m,d)&=\sum_{d|i,i|g}^{m}\mu(\frac{i}{d})G(i)\\ &=\sum_{d|i,i|g}^{m}\mu(\frac{i}{d})\lfloor\frac{m}{i}\rfloor\\g(m,1)&=\sum_{i|g}^{m}\mu(i)\lfloor\frac{m}{i}\rfloor\end{align*}$

这样，对于g，我们只需要用到gcd为1的，所以我们不妨把第二个参数去掉。整理一下，最后的答案就是：

$\large ans=\sum_{d=1}^{n}h(d)g(\lfloor\frac{n}{d}\rfloor)$

对于这个g(x)，根据莫比乌斯函数的性质，有效的i肯定不会是任意一个质因子的2次幂及以上，所以i一定是x的质因子的线性组合，因此我们可以把这个预处理出来。然后 $\lfloor\frac{n}{d}\rfloor$ 最多只有 $2\sqrt{\lfloor\frac{n}{d}\rfloor}$ 个，可以分块求和。假设 $\lfloor\frac{n}{d}\rfloor$ 的质因子数为cnt，那么计算g部分的开销就是 $O(2^{cnt}\sqrt{n})$ ，本题cnt最大为9，完全可以接受。那么问题的关键就是如何求h(d)的前缀和了。

我们发现，如果令 $H(d)=(\frac{m}{d})^k$ ，那么h(d)就是H(d)和 $\mu(d)$ 的迪利克雷卷积，而H(d)和 $\mu(d)$ 是显然具有积性的。所以说我们可以用积性函数的性质，构造线性筛来求解h(d)的前缀和。但是注意到，本题的数据范围是 $10^9$ ，而且还有多组数据，即使是线性的筛法也无法满足条件。所以我们这里考虑用杜教筛。

杜教筛了解一下：https://blog.csdn.net/skywalkert/article/details/50500009

简单来说就是，利用迪利克雷卷积的恒等变换，使得一个原本不容易求的积性数论函数的前缀和，变成两个容易求的积性数论函数运算，最后转化成 $S(n)=A(n)-\sum_{i=2}^{n}S(n/i)$ 的形式，其中A(n)表示辅助的容易求和的积性数论函数的前缀和。之后对于前 $\large n^{\frac{2}{3}}$ 的S(n)，用构造线性筛直接打表计算；对于后面的大的部分，利用上面的式子分块记忆化搜索计算。可以证明这样子做的复杂度是O( $\large n^{\frac{2}{3}}$ )的。

对于本题，令 $S(n)=\sum_{i=1}^{n}h(i)$ ，我们可以这么推导：

$\large \begin{align*}h(i)&=(H*\mu)(i) \\(h*I)(i)&=(H*\mu*I)(i)\\ &=H(d)=\sum_{x=1}^{i}x^k\\ \sum_{i=1}^{n}(h*I)(i)&=\sum_{i=1}^{n}H(i)\\ \sum_{i=1}^{n}\sum_{j|i}h(\frac{i}{j})I(j)&= \sum_{x=1}^{n}x^k \\ \sum_{j=1}^{n}I(j)\sum_{i=1}^{n/j}h(i)&= \sum_{x=1}^{n}x^k\\ \sum_{j=1}^{n}S(\frac{n}{j})&= \sum_{x=1}^{n}x^k\\ S(n)&=\sum_{x=1}^{n}x^k- \sum_{j=2}^{n}S(\frac{n}{j})\end{align*}$

最后这个东西满足杜教筛的形式，关于前面这个幂和，我们同样有方法计算：https://www.zybuluo.com/yang12138/note/848419

本题的话选用伯努利数的方法来计算幂和，即 $\sum_{x=1}^{n}x^k=\frac{1}{k+1}\sum_{i=1}^{k+1}C_{k+1}^iB_{k+1-i}(n+1)^i$ 。经过曲折之后，我们就可以在O( $\large n^{\frac{2}{3}}$ )的时间复杂度内求出这个h(d)的前缀和S(d)。最后的答案 $\large ans=\sum_{d=1}^{n}h(d)g(\lfloor\frac{n}{d}\rfloor)$ ，分成两部分分块求和即可。最后总的时间复杂度是 $O(n^{\frac{2}{3}}+512\sqrt{n})$ 。具体见代码：

#include<bits/stdc++.h>
#define LL long long
#define mod 1000000007
#define pb push_back
#define lb lower_bound
#define ub upper_bound
#define INF 0x3f3f3f3f
#define sf(x) scanf("%d",&x)
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/assoc_container.hpp>
#define sc(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define clr(x,n) memset(x,0,sizeof(x[0])*(n+5))
#define file(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)

using namespace __gnu_pbds;
using namespace std;

const int N = 1e6 + 10;
const int K = 1e2 + 10;

int n,m,k,tot,S[N],C[K][K],p[N];
gp_hash_table<int,int> mp;
std::vector<int> pri_fac;
typedef pair<int,int> P;
LL B[K],invk,pw[N];
std::vector<P> fac;
bool isp[N];

LL qpow(LL x,int n)
{
    LL res=1;
    while(n)
    {
        if(n&1) res=res*x%mod;
        x=x*x%mod; n>>=1;
    }
    return res;
}

void init()
{
    C[0][0]=1;
    for(int i=1;i<K;i++) C[i][0]=1;
    for(int i=1;i<K;i++)
        for(int j=1;j<K;j++)
            C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
    B[0]=1;
    for(int i=1;i<K;i++)
    {
        for(int j=0;j<i;j++)
            B[i]+=C[i+1][j]*B[j]%mod;
        B[i]%=mod; B[i]=(mod-B[i])*qpow(i+1,mod-2)%mod;
    }
}

void sieve(int n)
{
    int sz=0; S[1]=1;
    for(int i=2;i<n;i++)
    {
        if (!isp[i])
        {
            p[++sz]=i;
            pw[i]=qpow(i,k);
            S[i]=pw[i]-1;
        }
        for(int j=1;j<=sz&&p[j]*i<n;j++)
        {
            int x=i*p[j]; isp[x]=1;
            if (i%p[j]==0)
            {
                S[x]=S[i]*pw[p[j]]%mod;
                break;
            } else S[x]=S[i]*(pw[p[j]]-1)%mod;
        }
    }
    for(int i=2;i<n;i++) S[i]=(S[i-1]+S[i])%mod;
}

int powsum(int x)
{
    if (k==0) return x;
    LL res=0,pw=1;
    for(int i=1;i<=k+1;i++)
    {
        pw=pw*(x+1)%mod;
        res+=C[k+1][i]*B[k+1-i]%mod*pw%mod;
    }
    res%=mod;
    return res*invk%mod;
}

int s(int x)
{
    if (x<tot) return S[x];
    if (mp[x]) return mp[x];
    LL res=powsum(x);
    for(int l=2,r;l<=x;l=r+1)
    {
        r=x/(x/l);
        res-=(r-l+1)*(LL)s(x/l)%mod;
    }
    res=res%mod+mod;
    return mp[x]=res%mod;
}

LL cal(int x)
{
    LL res=0;
    for(auto i:fac)
    {
        if (i.first>x) break;
        res+=(x/i.first)*(i.second&1?-1:1);
    }
    return res%mod;
}

int main()
{
    int T; sf(T);
    init(); int AC=1;
    while(T--)
    {
        sf(n); sf(m);
        int g=0; k=0; mp.clear();
        for(int i=1;i<=n;i++)
        {
            int x; sf(x);
            if(x==-1)k++;else g=__gcd(g,x);
        }
        sieve(tot=ceil(pow(m,2.0/3)));
        invk=qpow(k+1,mod-2);
        if (g==0)
        {
            printf("Case #%d: %d\n",AC++,s(m));
            continue;
        }
        LL ans=0;
        fac.clear();
        pri_fac.clear();
        for(int i=2;i*i<=g;i++)
        {
            if (g%i) continue;
            pri_fac.pb(i);while(g%i==0) g/=i;
        }
        if (g>1) pri_fac.pb(g);
        int up=1<<pri_fac.size();
        for(int i=0;i<up;i++)
        {
            int cnt=0,d=1;
            for(int j=0;j<pri_fac.size();j++)
                if (i&(1<<j)) cnt++,d*=pri_fac[j];
            fac.pb(P(d,cnt));
        }
        sort(fac.begin(),fac.end());
        int pre=0,cur;
        for(int l=1,r;l<=m;l=r+1)
        {
            r=m/(m/l); cur=s(r);
            ans+=(cur-pre)*cal(m/l)%mod;
            pre=cur;
        }
        ans%=mod;
        printf("Case #%d: %lld\n",AC++,(ans+mod)%mod);
    }
    return 0;
}

HDU 6439 2018CCPC网络赛 Congruence equationI（杜教筛 + 莫比乌斯反演 + 伯努利数）

猜你喜欢