两个变数之间的关系不一定是简单的线性关系,可能是多种多样的曲线关系。
X在某一区间上,X和Y的关系有可能用线性描述,但X可能取值的区间而言 ,可能是非线性。
两个变数呈现曲线关系的回归称曲线回归(curvilinear regression)或非线性回归(non-linear regression)。
以最小二乘法分析曲线关系资料在数量变化上的特征和规律,称为曲线回归分析或非线性回归分析。
曲线角度看,线性回归仅是其中的一个特例:直线可看成是曲率为0的曲线。
一、曲线的类型与特点
根据曲线的性质和特点可大致分为6类:指数函数曲线,对数,幂函数,双曲,S型和多项式曲线。
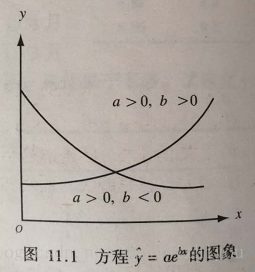
(1)指数函数曲线
指数函数(x 作为指数出现)方程形式: 参数b一般用来描述增长或衰减的速度
,当 a>0、b>0时,y随x的增大而增大(增长),曲线凹向上;
当 a>0、b<0时,y随x的增大而减小(衰减),曲线也是凹向上。
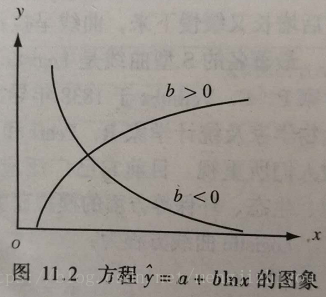
(2)对数函数曲线
对数函数(x 作为自然对数出现)方程形式: (x>0)
对数函数表示:x变数的较大变化可引起y变数的较小变化。
b>0时,y随x的增大而增大,曲线凸向上;
b<0时,y随x的增大而减小,曲线凹向上。
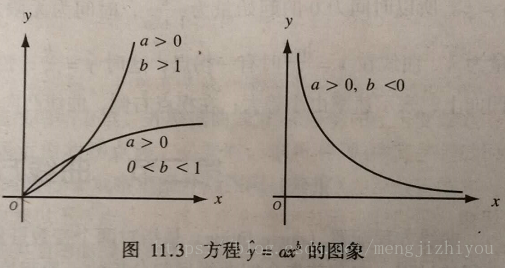
(3)幂函数曲线
对数函数(y是x某次幂的函数)方程形式:
当 a>0、b>1时,y随x的增大而增大(增长),曲线凹向上;
当 a>0、0<b<1时,y随x的增大而增大(增长),但变化缓慢,曲线凸向上;
当 a>0、b<0时,y随x的增大而减小,曲线凹向上,且以x,y轴为渐近线。
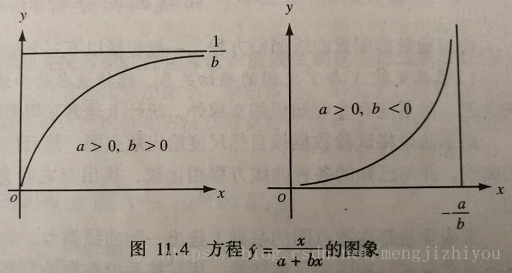
(4)双曲函数曲线:变形双曲线
方程形式:i:
ii:
iii:
, 该曲线通过原点(0,0)
当 a>0、b>0时,y随x的增大而增大,但速率趋小,曲线凸向上,并向y=1/b渐进;
当 a>0、b<0时,y随x的增大而增大,速率趋大,曲线凹向上,并向x=-a/b渐进。
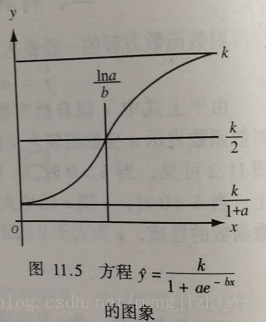
(5)S型曲线
主要描述动、植物的自然生长过程,又称生长曲线。
生长过程的基本特点是开始增长较慢,而在以后的某一范围内迅速增长,达到一定的限度后增长又缓慢下来,曲线呈拉长的‘S’型曲线。‘注明的S’型曲线是Logistic生长曲线。
Logistic曲线方程: (a、b、k均大于0)
x=0, ; x
,
;
所以时间为0的起始量为 , 时间为无限延长的终极量为 k
曲线时有一个拐点,这时
,恰好是终极量k的一半
拐点左侧,曲线凹向上,速率由小趋大;拐点右侧,曲线凸向上,速率由大趋小。
二、曲线方程的配置
曲线方程配置(curve fitting):指对两个变数资料进行曲线回归分析,获得一个显著的曲线方程的过程。
1、曲线回归分析的一般程序
由试验数据配置曲线回归方程,包括以下三个步骤:
(1)根据变数X和Y之间的确切关系,选择适当的曲线类型
确定曲线类型是曲线回归分析的关键。除了应有专业知识支撑外,统计上通常采用图示法和直线化法辅助选择。
图示法:将试验数据按自然尺度绘出散点图,然后按照散点趋势画出反映它们之间变化规律的曲线,并与已知的各种曲线方程相比较,找出与之最为相似的曲线图形,作为选定的曲线类型。
直线化法:是在散点图的基础上选出一种曲线类型,对该曲线方程进行尺度转换使之直线化,再将原数据进行相同的尺度转换,用转换后的数据绘出新的散点图。若此散点图具有直线趋势,即表明选取的曲线类型是恰当的。
(2)对选定的曲线类型,在线性化后按最小二乘法原理配置直线回归方程,并作显著性测验
求得两变数或转换后的新变数间的线性相关系数 。
若此 不显著,则分析结束,表明所选曲线方程不适合;
若 显著,则表明所选曲线方程在统计上是恰当的,可继续求解回归统计数,获得直线回归方程。
(3)将直线回归方程转换成相应的曲线方程,并对有关统计参数作出推断
获得显著的直线回归方程后,可直接反转 换成相应的曲线回归方程,并根据曲线方程的特性估计有关参数,包括回归参数、极小值、极大值、渐进值和拐点等。必要时,可利用曲线方程进行x观察范围内的预测(内插),或在论据充足时进行x观察范围外的预测(外推)。
应用上述程序配置曲线方程,注意点如下:
(1)若同一资料用两种或两种以上不同类型的曲线方程配置,结果均为显著,则需选择其中最佳的曲线方程。判别的统计标准是不同曲线方程下离回归平方和 的大小,
最小者当选。也可直接根据直线化后的
的绝对值大小直接确定。
(2)若进行转换后仍无法找出显著的直线化方程,可考虑采用多项式逼近。
(3)一些方程无法进行直线化转换,此时可直接采用最小二乘法拟合。所有曲线方程均可采用最小二乘法直接拟合,且一般预期可比线性化方法获得更好的拟合度。
2、指数曲线方程 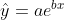 的配置
的配置
若 y 观察值都大于 0,则可对两边取自然对数:
令, 则
与 x 的线性相关系数:
若显著,
3、幂函数曲线方程 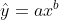 的配置
的配置
若 y 和 x 都大于0时可线性化:
令,
, 则
与 x 的线性相关系数:
若显著,
4、Logistic曲线方程的配置
(a、b、k均大于0)
要对方程进行线性化处理,必须首先确定k值。
根据k是生长过程中的终极量的特点,有两种方法估计:
(1)如果y是累积频率,k=100%
(2)如果y是生长量或繁殖量,可取3对观察值 ,
,
分别带入方程得到联立方程:
令 ,则可解得:
有了 k 的估值后,将方程移项并取自然对数得:
令 ,可得直线回归方程:
y和x对于Logistic方程的符合度可由 和x的相关系数给出:
若显著,