曲线回归------（二）多项式回归

一、多项式回归方程

（1）多项式回归方程式

当两个变数间的曲线关系很难确定时，可用多项式逼近，称多项式回归（polynomial regression）。

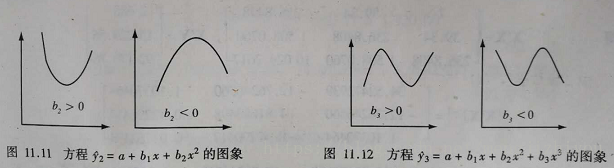
最简单的多项式是二次多项式，方程为： $\hat{y}_{2}=a+b_{1}x+b_{2}x^{2}$

三次多项式方程为： $\hat{y}_{3}=a+b_{1}x+b_{2}x^{2}+b_{3}x^{3}$ 具有两个弯曲和一个拐点

多项式方程的一般形式： $\hat{y}_{k}=a+b_{1}x+b_{2}x^{2}+...+b_{k}x^{k}$

特点：具有k-1个弯曲（k-1个极值）和k-2个拐点的曲线

多项式回归方程通常只能用于描述试验范围内Y依X的变化关系，外推一般不可靠。

（2）多项式方程次数的初步确定

两个变数的 n 对观察值按 $\hat{y}_{k}=a+b_{1}x+b_{2}x^{2}+...+b_{k}x^{k}$ 配置多项式方程时，最多可配到k=n-1次多项式。k 越大，包含的统计数越多，计算和解释越复杂。

一个多项式回归方程应取多少次为宜，可根据资料的散点图做出初步选择。散点所表现的曲线趋势的峰数+谷数+1，即为多项式回归方程的次数。若散点波动较大或峰谷两侧不对称，可再高一次。

（3）多项式回归统计数的计算

一般采用类似于多元线性回归的方法求解多项式回归的统计数。

对于 $\hat{y}_{k}=a+b_{1}x+b_{2}x^{2}+...+b_{k}x^{k}$ ，令 $x_{1}=x,x_{2}=x^{2},...,x_{k}=x^{k}$ ,则该式可化为：

$\hat{y}_{k}=a+b_{1}x_{1}+b_{2}x_{2}+...+b_{k}x_{k}$

（4）多项式回归方程的估计标准误

在多项式回归分析中，y变数的总平方和 $SS_{y}$ 可分解为回归和离回归两部分：

$SS_{y}=U_{k}+Q_{k}$

$U_{k}$ 为k次多项式的回归平方和，即Y变数总变异能为X的k次多项式所说明的部分；

$Q_{k}$ 为k次多项式的离回归平方和。

$SS_{y}=Y'Y-(1'Y)^{2}/n$

$Q_{k}=Y'Y-b'X'Y$

$U_{k}=b'X'Y-(1'Y)^{2}/n=SS_{y}-Q_{k}$

k次多项式的离回归标准误： $s_{y/x,x^{2},...,x^{k}}$ , 可定义为：

$s_{y/x,x^{2},...,x^{k}}=\sqrt{\frac{Q_{k}}{n-(k+1)}}$ 这也是多项式回归方程的估计标准误

二、多项式回归的假设测验

包括三项内容：

a:总的多项式回归关系是否成立

b:能否以k-1次多项式代替k次多项式，即是否有必要配到k次式

c:在一个k次多项式中，X的一次分量项、二次分量项、...、k-1次分量项能否被略去（相应的自由度和平方和并入误差）

（1）多项式回归系数的假设测验

在多项式回归分析中，y变数的总平方和 $SS_{y}$ 可分解为回归和离回归两部分：

$SS_{y}=U_{k}+Q_{k}$

前者由X的各次分量项的不同所引起的，v=k;

后者与X的不同无关，具有v=n-(k+1),因此F值： $F=\frac{U_{k}/k}{Q_k/[n-(k+1)]}$ 可测验多项式回归关系的真实性。

同多元相关系数 $R_{y\cdot 12...m}$ 相类似，k次多项式的回归平方和占Y总平方和的比率的平方根值（记作 $R_{y\cdot x,x^2,...,x^k}$ ：相关指数），可用来表示Y和X的多项式的相关密切程度： $R_{y\cdot x,x^2,...,x^k}=\sqrt{U_k/SS_y}$

k次多项式的决定系数，即在Y的总变异中，可由X的k次多项式说明的部分所占的比率： $R_{y\cdot x,x^2,...,x^k}^{2}=U_k/SS_y$

（2）k次多项式必要性的假设测验

上述F测验是一个综合性的测验，它的显著并不能排除多项式方程中个别乃至若干分量项不显著的可能性。如果一个k次多项式中的k次项并不显著，可化繁为简，由（k-1）次方程描述Y和X的曲线关系。

k次多项式的回归平方和是 $U_{k}$ ，v=k; k-1次多项式的回归平方和是 $U_{k-1}$ ，v=k-1。

从回归误差的角度看，有必要测验多项式增加一次所用去的一个自由度，对于离回归平方和的减少（或回归平方和的增加）是否‘合算‘： $F=\frac{U_{k}-U_{k-1}}{Q_k/[n-(k+1)]}$ ，可测验k次多项式的适合性。

（3）各次分量项的假设测验

当（2）证实需要一个k次多项式时，仍有必要了解k次式中的其它各次分量项是否显著。与多元线性回归中偏回归关系的假设测验相类似，各次分量项的测验亦需先计算偏回归平方和 $U_{P_i}$ (自由度为1): $U_{P_i}=b_i^2/c_{(i+1)(i+1)}$

$F=\frac{U_{P_i}}{Q_k/[n-(k+1)]}$ 可测验 i 次分量是否显著。