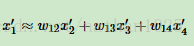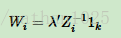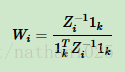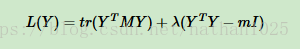LLE((locally linear embedding) 局部线性嵌入算法 Manifold Learning

LLE算法可以归结为三步:

（1）寻找每个样本点的k个近邻点；

（2）由每个样本点的近邻点计算出该样本点的局部重建权值矩阵；

（3）由该样本点的局部重建权值矩阵和其近邻点计算出该样本点的输出值。

    

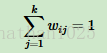
矩阵化：

=》

=》4式   =》

同时

=》根据拉格朗日乘子法

=》

=》求导 = 0可得

=》归一化后

此时我们得到了高维的权重系数，但是我们希望低维依然保持线性，如下

=》

tips：在线性代数中，一个n×n矩阵A的主对角线（从左上方至右下方的对角线）上各个元素的总和被称为矩阵A的迹（或迹数）

=》

=》拉格朗日乘子法

=》对Y求导可得=》MY=λY

=》即求M的的最小d个特征向量即可

=》于是我们可以想到，先求权重系数矩阵，然后再求M矩阵，最后获得M的d+1个特征向量组成的D矩阵，则完成了计算。

matlab

1：compute pairwise distances & find neighbour

distance = repmat(X2,N,1)+repmat(X2',1,N)-2*X'*X;

[sorted,index] = sort(distance);

neighborhood = index(2:(1+K),:);

2.计算权重矩阵

for i = 1:N
    A = X(:,neighborhood(:,i))-repmat(X(:,i),1,k); % 求A是把找到的5个相似块减去与其相似的低分辨率快的差值
    C = A'*A; % 计算局部协方差 求的是相似块之间的协方差 计算五个快的相关性
    C = C+eye(k,k)*tol*trace(C); % C+的部分迭代终止误差限 防止C过小 对数据正则化 为了数据的统一
    W(:,i) = C\ones(k,1); % 解方程Gw=e，高斯消去复杂度O(K^3)
    W(:,i) = W(:,i)/sum(W(:,i)); % 解向量w归一化 计算权重矩阵
end

3.M矩阵

M=sparse(1:N,1:N,ones(1,N),N,N,4*k*N); % M=(I-W)'(I-W); 稀疏矩阵

for i=1:N
    w=W(:,i);
    j=neighborhood(:,i);
    M(i,j)=M(i,j)-w';
    M(j,i)=M(j,i)-w;
    M(j,j) = M(j,j) + w*w';
end

4.计算非零对应的特征向量

[Y,eigenvals]=eigs(M,d+1,0,opts); % 返回 d+1 个最小特征值 指定选项结构 由大到小降序 0相当于sm 即取最小的特征值

https://blog.csdn.net/xiaozhouchou/article/details/51866685