偏置-方差分解
前面讨论的情况是假定了基函数的数量和形式,如果使用有限的数据集训练模型,使用最大似然或者最小平方,将会导致过拟合问题。但是通过限制基函数的数量避免过拟合,则会限制模型描述数据中的规律。如何选择合适的λ的值通过正则化来避免过拟合。
由第一章,我们知道–一旦确定了条件概率分布p(t|x),每一种的损失函数都能给出对应的最优预测结果。通常使用平方损失函数,此时的最优的预测由条件期望h(x)给出:
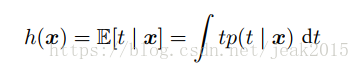
现在的问题是如何区分决策论中的平方损失函数及模型参数的最大似然估计中出现的平方和误差函数。
通过1.5.5的证明,平方损失函数的期望:
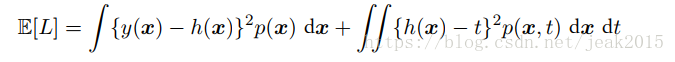
第二项的出现是根据数据的噪声造成,表示出期望损失能够达到的最小值。而第一项对函数y(x)选择有关,需要找到一个y(x)的解,使第一项最小。
假设我们使用由参数向量w控制的函数y(x,w)对y(x)建模:1.贝叶斯观点,模型的不确定性通过w的后验分布表示。频率派根据数据D对w进行点估计,然后试着通过以下方法表示估计的不确定性:
假设存在许多数据集,每个数据集大小为N,每个数据集都独立地从分布p(t,x)中抽取。对任意给定的数据集D,运用算法,得到预测函数y(x;D).不同数据集会给出不同的函数,从而给出不同的平方损失的值。
考虑上式第一项的被积函数,对于一个特定的数据集D,形式为
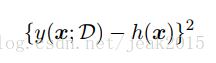
由于这个量与特定的数据集D相关,对所有的数据集取平方。通过在括号内加上再减去ED[y(x;D)],然后展开:

关于D求期望:
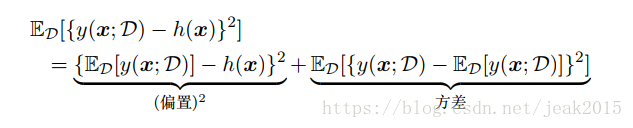
第一项:平方偏置,表示所有数据集的平均预测与预期的回归函数之间的差异;第二项,方差,度量了对于单独数据集,模型给出的解在平均值附近波动的情况,与表明了函数y(x;D)对于特定数据集的选择的敏感程度。
现在把展开式带回平方误差函数的期望公式中,得到对期望平方损失的分解:

我们的目标是最小化期望损失,它可以分解成偏置、方差和一个常数噪声项。对于灵活的模型,偏置小,方差大;对于固定的模型,偏置大,方差小。有着最优预测能力的模型能在偏置和方差之间取得最优的平衡。
产生100个数据集合,每个集合包含N=25个数据点,都独立从正弦曲线h(x)=sin(2πx)抽取。数据集编号l=1,2,….L,L=100。通过最小正则化误差函数拟合一个带有24个高斯基函数的模型,然后给出预测函数y(l)(x),如下图。
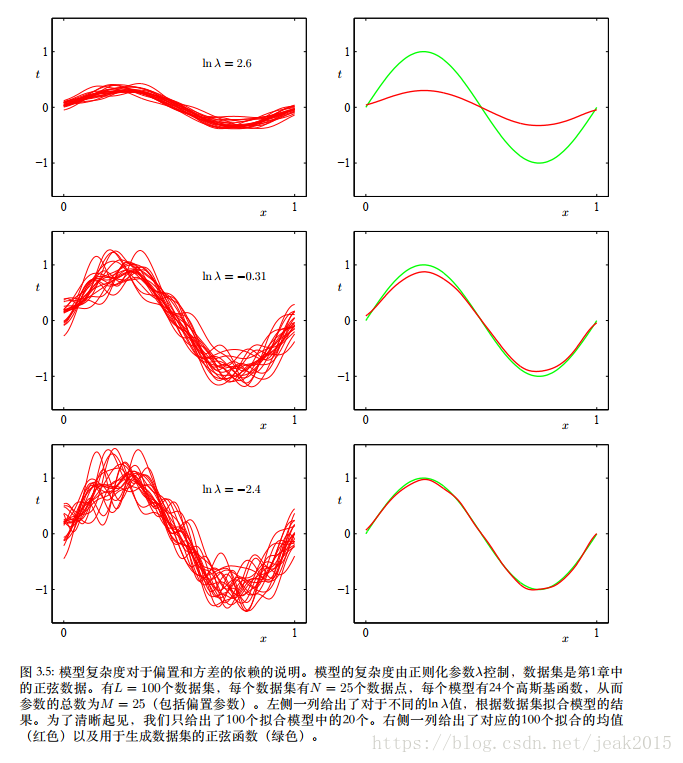
第一行对应着较大的正则化系数λ,这是方差很小,偏置大。相反的是,最后一行,正则化系数小,方差大,偏置小。如果把M=25这种模型的多个解进行平均,会产生对回归函数非常好的拟合。贝叶斯的核心就是将多各解加权平均—这是针对参数的后验分布。
平均预测的得出:
其中有概率分布p(x)加权的x的积分由来自哪个概率分布的有限数据点的加和近似。下图给出变量以及他们求和关于lnλ的图像。
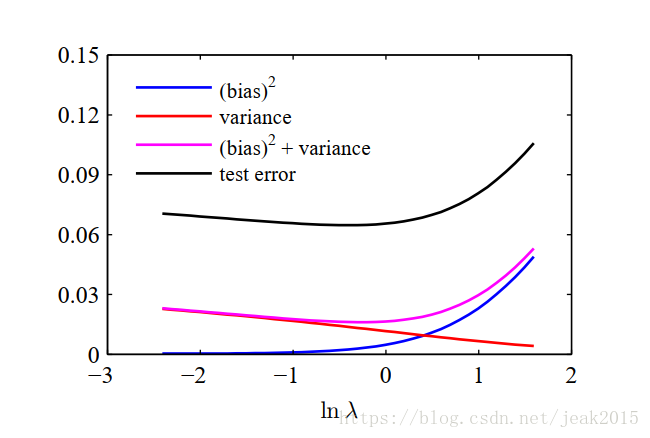
偏置-方差分解依赖对所有数据集求平均,而实际应用中只有一个观测集。如果拥有大量的已知规模的独立的训练数据集—将他们组合成一个大的训练集,这回降低给定复杂度的模型额过拟合程度。