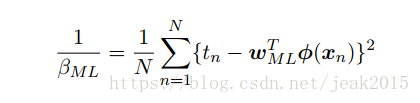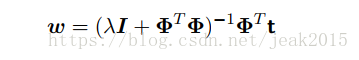3.回归的线性模型
3.1 线性及函数模型
回归问题的简单模型就是input的线性组合:
y(x,w) = w0 + w1x1 + w2x2 + wDxDx = (x1,x2,x3···xD).T
上式被称为线性回归。此模型的关键在于参数w0,w1,····wD,其是一个线性函数。同时它也可以是输入变量Xi的线性函数,就给模型带来了局限性。
于是进行扩展,将输入变量的固定的非线性函数进行线性组合,形式为:
y(x,w) = w0 + ∑wjφj(x)φj(x)被称为基函数。
参数w0使得数据中可以存在任意固定的偏置—偏置参数。定义一个虚”基函数”φ0(x)=1,于是上式变为:
y(x,w) = ∑wjφj(x) = w.T*φ(x)在许多模式识别的实际应用中,要对原始的数据进行某种固定形式的预处理或者特征抽取。
通过使用非线性基函数,能够让函数y(w,x)称为输入向量x 的非线性函数。
对于基函数的选择,例如:
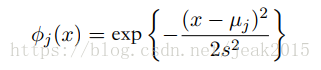
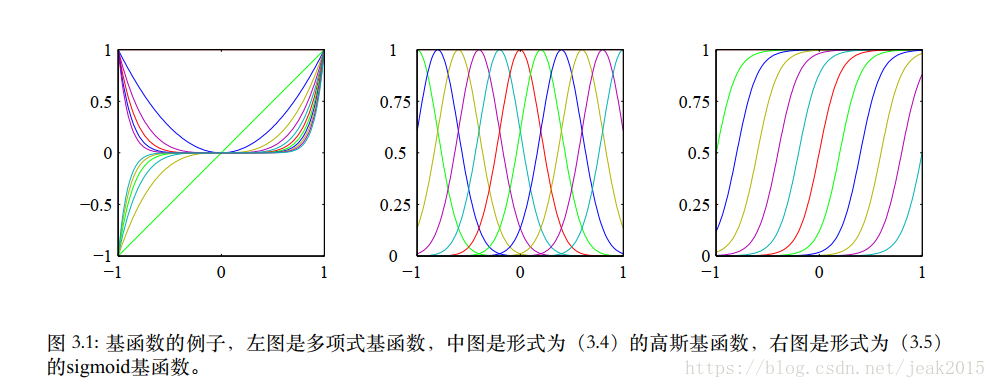
μj控制基函数在输入空间的位置,s控制基函数的空间大小,上式被称为高斯基函数。
sigmoid基函数:
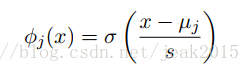

还有其他的基函数,例如傅里叶基函数、小波基函数。
三种基函数的图像:
3.1.1最大似然与最小平方
假设目标变量t有函数y(x,w)给出,同时附加了高斯噪声:
t = y(x,w) + εε是一个零均值的高斯随机分布,精度为(方差的倒数)为β:
p(t|x,w,β) = N(t|y(x,w),β^(-1))根据上式得到条件均值:
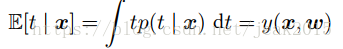
现在输入输入集X ={x1,x2,…xN},所对应的目标值为{tN}={t1,t2,…tN},为一个列向量,记作t。得到下列似然函数:
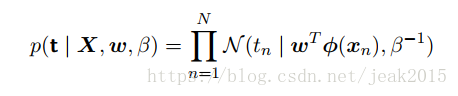
对似然函数取对数,并使用高斯分布的标准条件,得到:
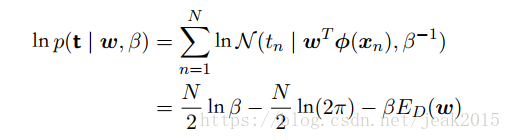
其中平方和误差函数为:
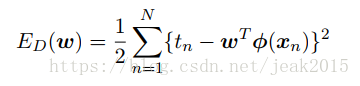
此时可以用最大似然方法求解w,β。首先计算w。对log(似然函数)求w的梯度:
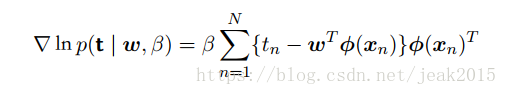
在第一章中当在条件高斯分布噪声分布的情况下,线性模型的似然函数的最大化 == 平方和误差函数的最小化,就得到了上式。
令这个导数为零,求解w的值:
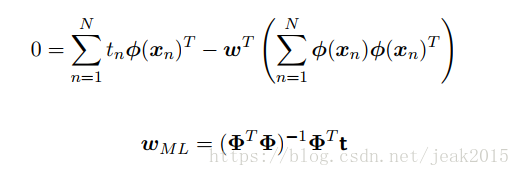
这被称为最小平方问题的规范矩阵。φ为N*M矩阵——设计矩阵。其中的元素是有输入向量通过基函数求得:
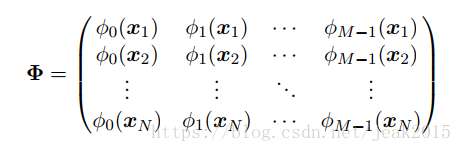
当求出w后,现在进行就算求得w0和β:
显式写出偏置参数:
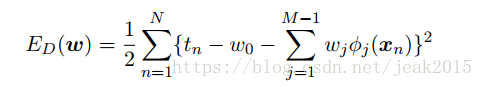
对上式关于w0求导,并为零:
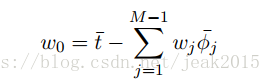
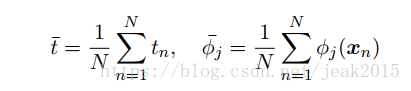
由此可以看出w0补偿了目标值的平均值(训练集)与基函数的值的平均值的加权求和之间的差。
同样的,求有关于β的梯度,并为零,求得β 的值为:
3.1.2 最小平方的几何描述
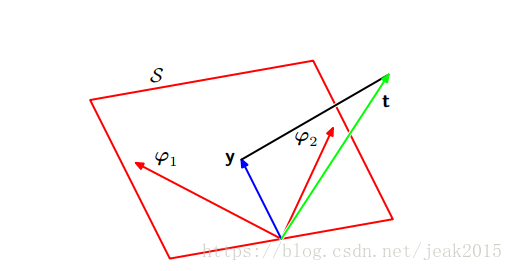
设计一个N维空间,坐标轴由tN给出,t={t1,t2,…,tN}.T是一个列向量。每个在N个数据点处估计的基函数Φj(xn)表示在空间中的向量,记作φj。φj对应于Φ的第j列,Φ(xn)对应于Φ的第i行。如果基函数的数量M小于数据点的数量N,则M个向量φj会扩展成一个M维的子空间S。定义y是一个N维向量,第n个元素为y(xn,w)。y是由φj任意线性组合,就决定了它的位置任意存在。则平方和误差函数==y与t之间的平方欧氏距离。w的最小平方解对应于子空间S的与t最近的y的选择。由图可知,w的解对应于t在S上的正交投影。
notice: y是由ΦWml给出。
3.1.3顺序学习
上面提到最大似然解的求解过程中涉及到一次处理整个数据集。当数据集相当大时,批量计算的计算量时很大的。顺序算法中,每次只考虑一个数据点,模型的参数在每次观测到一个数据后进行更新。
下面讲解顺序梯度下降。
如果误差函数由数据点的和组成E= ∑En,在观测到模式n后,随机梯度下降算法使用下式更新参数w:
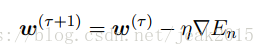
τ为迭代次数,η为学习率。w被初始化某个起始方向w(0).对于平方和误差函数:
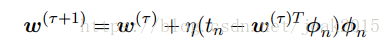
Φn=Φ(xn).被称为最小均方法。η需要仔细选择,确保收敛。
3.1.4正则化最小平方
通过添加正则项,抑制过拟合。则需要最小化的总的误差函数为
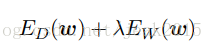
λ为正则化系数,控制数据相关的误差Ed(w)和正则化项Ew(w)的相对重要性。正则化项的一个简单的形式为权向量的各个元素的平方和:
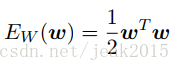
则平方和误差函数变成为下式:
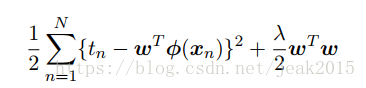
这种正则化项的选择方法被称为权值衰减。在顺序学习中,倾向于让权值向领的方向衰减。再介绍参数收缩,此方法中把参数的值向零的方向收缩。令上式关于w的梯度为零,求解出w:
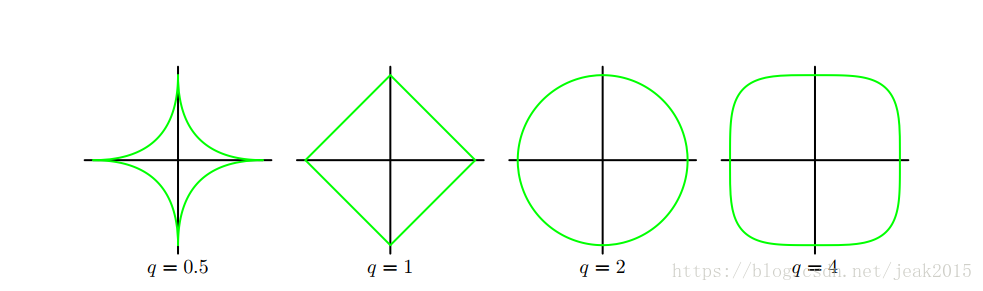
通常使用一般的正则化项,此时误差函数形式为:
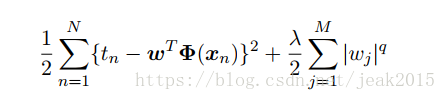
q=2的情况读英语二次正则化项。下图给出q不同值的轮廓线。
3.1.5多个输出
现在考虑K>1个目标变量。将这些目标聚集,记作t。对t的每个分量,引入一个不同的基函数集合,进而变成多个独立的回归问题。而常用的是对目标向量的所有分量使用一组相同的基函数建模:
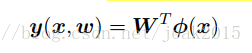
y为一个k维列向量,W为M*K参数矩阵,Φ(x)是一个M维的列向量,每个元素为Φj(x),Φ0(x)=1。
添加条件:目标向量的条件概率分布是一个各向同性的高斯分布:
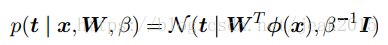
T={t1,t2,…tN}为N*K的矩阵,X={x1,x2,….xN},则对数似然函数为:
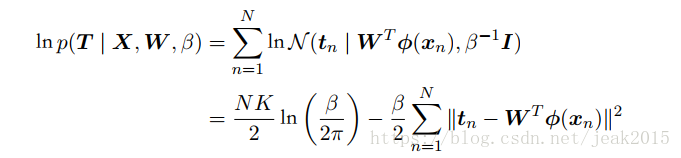
求解w,最大化对数似然函数:
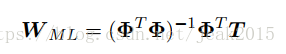
如果考虑对每个目标变量tk,则wk则有:
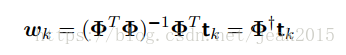
tk是一个N维列向量,元素为tnk。