数据结构好像忘了看关于图的,然后只说了,深度优先遍历和广度优先遍历。
原文地址:
http://www.cnblogs.com/skywang12345/p/3711516.html
Dijkstra算法
1.定义概览
Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。Dijkstra算法是很有代表性的最短路径算法,在很多专业课程中都作为基本内容有详细的介绍,如数据结构,图论,运筹学等等。注意该算法要求图中不存在负权边。
问题描述:在无向图 G=(V,E) 中,假设每条边 E[i] 的长度为 w[i],找到由顶点 V0 到其余各点的最短路径。(单源最短路径)
2.算法描述(算法很抽象,直接看例子)
1)算法思想:设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径 , 就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
(1) 初始时,S只包含起点s;U包含除s外的其他顶点,且U中顶点的距离为”起点s到该顶点的距离”[例如,U中顶点v的距离为(s,v)的长度,然后s和v不相邻,则v的距离为∞]。
(2) 从U中选出”距离最短的顶点k”,并将顶点k加入到S中;同时,从U中移除顶点k。
(3) 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离,是由于上一步中确定了k是求出最短路径的顶点,从而可以利用k来更新其它顶点的距离;例如,(s,v)的距离可能大于(s,k)+(k,v)的距离。
(4) 重复步骤(2)和(3),直到遍历完所有顶点。
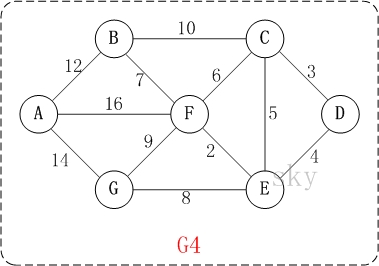
以上图G4为例,来对迪杰斯特拉进行算法演示(以第4个顶点D为起点)。
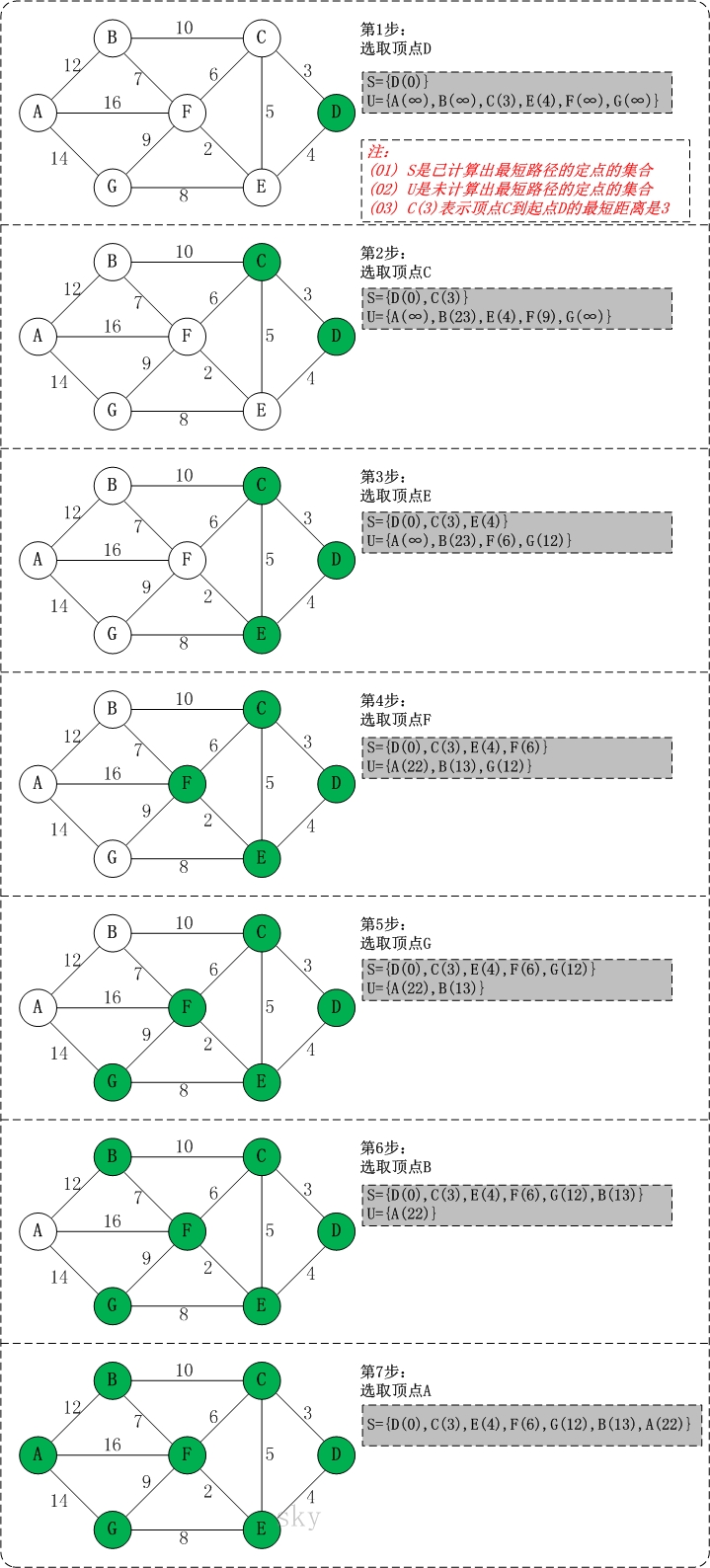
初始状态:S是已计算出最短路径的顶点集合,U是未计算除最短路径的顶点的集合!
第1步:将顶点D加入到S中。
此时,S={D(0)}, U={A(∞),B(∞),C(3),E(4),F(∞),G(∞)}。 注:C(3)表示C到起点D的距离是3。
第2步:将顶点C加入到S中。
上一步操作之后,U中顶点C到起点D的距离最短;因此,将C加入到S中,同时更新U中顶点的距离。以顶点F为例,之前F到D的距离为∞;但是将C加入到S之后,F到D的距离为9=(F,C)+(C,D)。
此时,S={D(0),C(3)}, U={A(∞),B(23),E(4),F(9),G(∞)}。
第3步:将顶点E加入到S中。
上一步操作之后,U中顶点E到起点D的距离最短;因此,将E加入到S中,同时更新U中顶点的距离。还是以顶点F为例,之前F到D的距离为9;但是将E加入到S之后,F到D的距离为6=(F,E)+(E,D)。
此时,S={D(0),C(3),E(4)}, U={A(∞),B(23),F(6),G(12)}。
第4步:将顶点F加入到S中。
此时,S={D(0),C(3),E(4),F(6)}, U={A(22),B(13),G(12)}。
第5步:将顶点G加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12)}, U={A(22),B(13)}。
第6步:将顶点B加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12),B(13)}, U={A(22)}。
第7步:将顶点A加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12),B(13),A(22)}。
此时,起点D到各个顶点的最短距离就计算出来了:A(22) B(13) C(3) D(0) E(4) F(6) G(12)。
例子中的B{13}写错了
java代码:
public class dijkstraMethod {
private final int INF = Integer.MAX_VALUE;
int [][] Matrix;
char[] Nodes;
public dijkstraMethod(char[] Nodes, int [][] Matrix)
{
this.Nodes = Nodes;
this.Matrix = Matrix;
}
/**
*
* @param node
* @param distance
*/
public void dijkstra(int node, int [] distance)
{
boolean [] flag = new boolean[Nodes.length];
for(int i = 0 ;i<Nodes.length;i++)
{
flag[i] = false;
distance[i] = Matrix[node][i];
}
flag[node] = true;
distance[node] = 0;
int k = 0;
for(int i = 1;i<Nodes.length;i++)
{
int min = INF;
for(int j = 0;j<Nodes.length;j++)
{
if(!flag[j]&&distance[j] < min)
{
k = j;
min = distance[j];
}
}
flag[k] = true;
for(int j = 0;j<Nodes.length;j++)
{
int len = Matrix[k][j] ==INF?INF:min+Matrix[k][j];
if(!flag[j]&&len<distance[j])
distance[j] = len;
}
}
System.out.printf("Dijkstra(%c): \n", Nodes[node]);
for(int i = 0; i<Nodes.length;i++)
{
System.out.printf(" shortest(%c, %c) = %d\n", Nodes[node],Nodes[i], distance[i]);
}
}
public static void main(String[] args) {
int INF = Integer.MAX_VALUE;
char[] Nodes = {'A', 'B', 'C', 'D', 'E'};
int matrix[][] = {
/*A*//*B*//*C*//*D*/
/*A*/ {0,1,5,INF,INF},
/*B*/ {1,0,2,4,INF},
/*C*/ {5,2,0,1,1},
/*D*/ {INF,4,1,0,2},
{INF,INF,1,2,0}
};
int[] dist = new int[Nodes.length];
dijkstraMethod dijkstra = new dijkstraMethod(Nodes, matrix);
dijkstra.dijkstra(2, dist);
}
}