详解神经网络的前向传播和反向传播
本篇博客是对Michael Nielsen所著的《Neural Network and Deep Learning》第2章内容的解读,有兴趣的朋友可以直接阅读原文Neural Network and Deep Learning。
对神经网络有些了解的人可能都知道,神经网络其实就是一个输入
X
到输出
Y
的映射函数:
f(X)=Y
,函数的系数就是我们所要训练的网络参数
W
,只要函数系数确定下来,对于任何输入
xi
我们就能得到一个与之对应的输出
yi
,至于
yi
是否符合我们预期,这就属于如何提高模型性能方面的问题了,本文不做讨论。
那么问题来了,现在我们手中只有训练集的输入
X
和输出
Y
,我们应该如何调整网络参数
W
使网络实际的输出
f(X)=Y^
与训练集的
Y
尽可能接近?
在开始正式讲解之前,让我们先对反向传播过程有一个直观上的印象。反向传播算法的核心是代价函数
C
对网络中参数(各层的权重
w
和偏置
b
)的偏导表达式
∂C∂w
和
∂C∂b
。这些表达式描述了代价函数值
C
随权重
w
或偏置
b
变化而变化的程度。到这里,BP算法的思路就很容易理解了:如果当前代价函数值距离预期值较远,那么我们通过调整
w
和
b
的值使新的代价函数值更接近预期值(和预期值相差越大,则
w
和
b
调整的幅度就越大)。一直重复该过程,直到最终的代价函数值在误差范围内,则算法停止。
BP算法可以告诉我们神经网络在每次迭代中,网络的参数是如何变化的,理解这个过程对于我们分析网络性能或优化过程是非常有帮助的,所以还是尽可能搞透这个点。我也是之前大致看过,然后发现看一些进阶知识还是需要BP的推导过程作为支撑,所以才重新整理出这么一篇博客。
前向传播过程
在开始反向传播之前,先提一下前向传播过程,即网络如何根据输入
X
得到输出
Y
的。这个很容易理解,粗略看一下即可,这里主要是为了统一后面的符号表达。
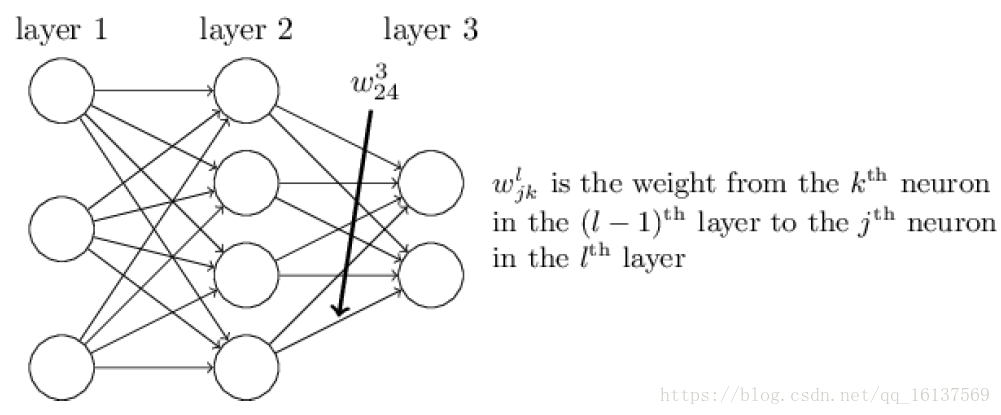
记
wljk
为第
l−1
层第
k
个神经元到第
l
层第
j
个神经元的权重,
blj
为第
l
层第
j
个神经元的偏置,
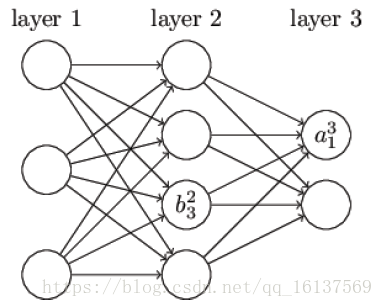
alj
为第
l
层第
j
个神经元的激活值(激活函数的输出)。不难看出,
alj
的值取决于上一层神经元的激活:
alj=σ(∑kwljkal−1k+blj)(1)
将上式重写为矩阵形式:
al=σ(wlal−1+bl)(2)
为了方便表示,记
zl=wlal−1+bl
为每一层的权重输入,
(2)
式则变为
al=σ(zl)
。
利用
(2)
式一层层计算网络的激活值,最终能够根据输入
X
得到相应的输出
Y^
。
反向传播过程
反向传播过程中要计算
∂C∂w
和
∂C∂b
,我们先对代价函数做两个假设,以二次损失函数为例:
C=12n∑x∥y(x)−aL(x)∥2(3)
其中
n
为训练样本
x
的总数,
y=y(x)
为期望的输出,即ground truth,
L
为网络的层数,
aL(x)
为网络的输出向量。
假设1:总的代价函数可以表示为单个样本的代价函数之和的平均:
C=1n∑xCx Cx=12∥y−aL∥2(4)
这个假设的意义在于,因为反向传播过程中我们只能计算单个训练样本的
∂Cx∂w
和
∂Cx∂b
,在这个假设下,我们可以通过计算所有样本的平均来得到总体的
∂C∂w
和
∂C∂b
假设2:代价函数可以表达为网络输出的函数
costC=C(aL)
,比如单个样本
x
的二次代价函数可以写为:
Cx=12∥y−aL∥2=12∑j(yj−aLj)2(5)
反向传播的四个基本方程
权重
w
和偏置
b
的改变如何影响代价函数
C
是理解反向传播的关键。最终,这意味着我们需要计算出每个
∂C∂wljk
和
∂C∂blj
,在讨论基本方程之前,我们引入误差
δ
的概念,
δlj
表示第
l
层第
j
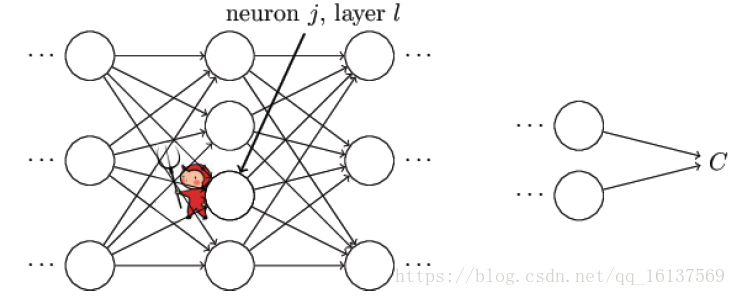
个单元的误差。关于误差的理解,《Neural Network and Deep Learning》书中给了一个比较形象的例子。
如上图所示,假设有个小恶魔在第
l
层第
j
个单元捣蛋,他让这个神经元的权重输出变化了
Δzlj
,那么这个神经元的激活输出为
σ(zlj+Δzlj)
,然后这个误差向后逐层传播下去,导致最终的代价函数变化了
∂C∂zljΔzlj
。现在这个小恶魔改过自新,它想帮助我们尽可能减小代价函数的值(使网络输出更符合预期)。假设
∂C∂zlj
一开始是个很大的正值或者负值,小恶魔通过选择一个和
∂C∂zlj
方向相反的
Δzlj
使代价函数更小(这就是我们熟知的梯度下降法)。随着迭代的进行,
∂C∂zlj
会逐渐趋向于0,那么
Δzlj
对于代价函数的改进效果就微乎其微了,这时小恶魔就一脸骄傲的告诉你:“俺已经找到了最优解了(局部最优)”。这启发我们可以用
∂C∂zlj
来衡量神经元的误差:
δlj=∂C∂zlj
下面就来看看四个基本方程是怎么来的。
1. 输出层的误差方程
δLj=∂C∂zLj=∂C∂aLj∂aLj∂zLj=∂C∂aLjσ′(zLj)(BP1)
如果上面的东西你看明白了,这个方程应该不难理解,等式右边第一项
∂C∂aLj
衡量了代价函数随网络最终输出的变化快慢,而第二项
σ′(zLj)
则衡量了激活函数输出随
zLj
的变化快慢。当激活函数饱和,即
σ′(zLj)≈0
时,无论
∂C∂aLj
多大,最终
δLj≈0
,输出神经元进入饱和区,停止学习。
(BP1)方程中两项都很容易计算,如果代价函数为二次代价函数
C=12∑j(yj−aLj)2
,则
∂C∂aLj=aLj−yj
,同理,对激活函数
σ(z)
求
zLj
的偏导即可求得
σ′(zLj)
。将(BP1)重写为矩阵形式:
δL=∇aC⊙σ′(zL)(BP1a)
⊙
为Hadamard积,即矩阵的点积。
2. 误差传递方程
δl=((wl+1)Tδl+1)⊙σ′(zl)(BP2)
这个方程说明我们可以通过第
l+1
层的误差
δl+1
计算第
l
层的误差
δl
,结合(BP1)和(BP2)两个方程,我们现在可以计算网络中任意一层的误差了,先计算
δL
,然后计算
δL−1
,
δL−2
,…,直到输入层。
证明过程如下:
δlj=∂C∂zlj=∑k∂C∂zl+1k∂zl+1k∂zlj=∑kδl+1k∂zl+1k∂zlj
因为
zl+1k=∑jwl+1kjalj+bl+1k=∑jwl+1kjσ(zlj)+bl+1k
,所以
∂zl+1k∂zlj=wl+1kjσ′(zlj)
,因此可以得到(BP2),
δlj=∑kwl+1kjδl+1kσ′(zlj)
3. 代价函数对偏置的改变率
∂C∂blj=∂C∂zlj∂zlj∂blj=∂C∂zlj=δlj(BP3)
这里因为
zlj=∑kwljkal−1k+blj
所以
∂zLj∂bLj=1
4. 代价函数对权重的改变率
∂C∂wljk=∂C∂zlj∂zLj∂wljk=∂C∂zljal−1k=al−1kδlj(BP4)
可以简写为
∂C∂w=ainδout(6)
,不难发现,当上一层激活输出接近0的时候,无论返回的误差有多大,
∂C∂w
的改变都很小,这也就解释了为什么神经元饱和不利于训练。
从上面的推导我们不难发现,当输入神经元没有被激活,或者输出神经元处于饱和状态,权重和偏置会学习的非常慢,这不是我们想要的效果。这也说明了为什么我们平时总是说激活函数的选择非常重要。
当我计算得到
∂C∂wljk
和
∂C∂blj
后,就能愉悦地使用梯度下降法对参数进行一轮轮更新了,直到最后模型收敛。
反向传播为什么快
回答这个问题前,我们先看一下普通方法怎么求梯度。以计算权重为例,我们将代价函数看成是权重的函数
C=C(w)
,假设现在网络中有100万个参数,我们可以利用微分的定义式来计算代价函数对其中某个权重
wj
的偏导:
∂C∂wj≈C(w+εej→)−C(w)ε(7)
然后我们算一下,为了计算
∂C∂wj
,我们需要从头到尾完整进行一次前向传播才能得到最终
C(w+εej→)
的值,要计算100万个参数的偏导就需要前向传播100万次,而且这还只是一次迭代,想想是不是特别可怕?
再反观反向传播算法,如方程(BP4)所示,我们只要知道
al−1k
和
δlj
就能计算出偏导
∂C∂wljk
。激活函数值
al−1k
在一次前向传播后就能全部得到,然后利用(BP1)和(PB2)可以计算出
δlj
,反向传播和前向传播计算量相当,所以总共只需2次前向传播的计算量就能计算出所有的
∂C∂wljk
。这比使用微分定义式求偏导的计算量少了不止一点半点,简直是质的飞跃。