深度学习与计算机视觉（四）反向传播及其直观理解

四、反向传播及其直观理解

4.1 引言

问题描述和动机：

1. 大家都知道，其实我们就是在给定的图像像素向量x和对应的函数$f(x)$，然后我们希望能够计算$f$在x上的梯度$\nabla f(x)$

2. 之所以要解决这个问题，是因为在神经网络中，$f$对应损失函数$L$，而输入$x$则对应训练样本数据和神经网络的权重$W$。通常我们认为训练数据是给定的，而权重是我们可以控制的变量。因此我们为了更新权重的等参数，使得损失函数值最小，我们通常是计算f 对参数W,b 的梯度。

4.2 高数梯度 、偏导基础

假如$f(x,y)=xy$，那么我们可以求这个函数对$x$和$y$的偏导：

$f(x,y)=xy→\frac{∂f}{∂x} =y , \frac{∂f}{∂y} =x$

解释：偏导数的含义是一个函数在给定变量所在维度，当前点附近的一个变化率，也就是：

$$\frac{df(x)}{dx} =lim_{ h →0}\frac{ f(x+h)−f(x)}{h}$$

每个维度/变量上的偏导，表示整个函数表达式，在这个值上的『敏感度』。

我们说的梯度$∇f$其实是一个偏导组成的向量，比如我们有$∇f=[∂f∂x ,∂f∂y ]=[y,x]$ 。即使严格意义上来说梯度是一个向量，但是大多数情况下，我们还是习惯直呼『x上的梯度』，而不是『x上的偏导』

4.3 复杂函数偏导的链式法则

假设有一个较为复杂一点的函数，比如$f(x,y,z)=(x+y)z$，虽然我们可以直接求偏导，但是我们用一个非直接的思路去求解一下偏导，以帮助我们直观理解反向传播中，如果我们用换元法，把函数拆分为两部分，$q=x+y$和$f=qz$，对于这两个部分，我们知道如何求解其变量上的偏导：

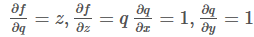
当然q是我们设定的一个变量，不关心其偏导值。

那『链式法则』告诉我们一个对上述偏导公式『串联』的方式，得到我们感兴趣的偏导数

$$\frac{∂f}{∂x} =\frac{∂f}{∂q}\cdot \frac{ ∂q}{∂x}$$

x = -2; y = 5; z = -4

# 前向计算
q = x + y # q becomes 3
f = q * z # f becomes -12

# 类反向传播:
# 先算到了 f = q * z
dfdz = q               # df/dz = q
dfdq = z               # df/dq = z
# 再算到了 q = x + y
dfdx = 1.0 * dfdq # dq/dx = 1 恩，链式法则
dfdy = 1.0 * dfdq # dq/dy = 1

链式法则的结果是，只剩下我们感兴趣的[dfdx,dfdy,dfdz]，也就是原函数在x,y,z上的偏导。这是一个简单的例子，之后的程序里面我们为了简洁，不会完整写出dfdq，而是用dq代替。

以下是这个计算的示意图：

4.4 反向传播的直观理解

反向传播的过程，实际上是一个由局部到全部的精妙过程。比如上面的电路图中，其实每一个『门』在拿到输入之后，都能计算2个东西：

• 输出值

• 对应输入和输出的局部梯度

而且很明显，每个门在进行这个计算的时候是完全独立的，不需要对电路图中其他的结构有了解。然而，在整个前向传输过程结束之后，在反向传播过程中，每个门却能逐步累积计算出它在整个电路输出上的梯度。

『链式法则』告诉我们每一个门接收到后向传来的梯度，同时用它乘以自己算出的对每个输入的局部梯度，接着往后传。

以上面的图为例，来解释一下这个过程。加法门接收到输入[-2, 5]同时输出结果3。因为加法操作对两个输入的偏导都应该是1。电路后续的乘法部分算出最终结果-12。在反向传播过程中，链式法则是这样做的：加法操作的输出3，在最后的乘法操作中，获得的梯度为-4，如果把整个网络拟人化，我们可以认为这代表着网络『想要』加法操作的结果小一点，而且是以4*的强度来减小。加法操作的门获得这个梯度-4以后，把它分别乘以本地的两个梯度(加法的偏导都是1)，1*-4=-4。如果输入x减小，那加法门的输出也会减小，这样乘法输出会相应的增加。

反向传播，可以看做网络中门与门之间的『关联对话』，它们『想要』自己的输出更大还是更小(以多大的幅度)，从而让最后的输出结果更大。