机器学习练习（四）——异常检测

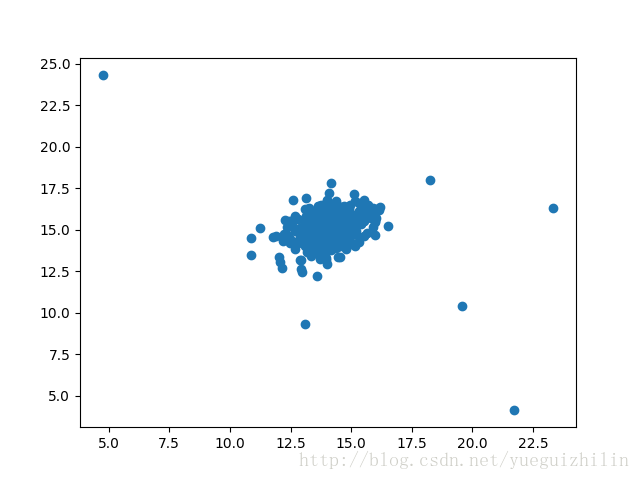
我们的任务是使用高斯模型来检测数据集中一个未标记（unlabeled）的样本是否应被视为异常。我们从一个简单的 2 维数据集开始，因此我们可以很容易地可视化这算法的工作原理。让我们导入数据并画出散点图。
#!/usr/bin/env python
# -*- coding:utf-8 -*-
# 使用高斯模型来检测数据集中一个未标记（unlabeled）的样本是否应被视为异常
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sb
from scipy.io import loadmat
from scipy import stats
# atplotlib inline

data = loadmat('data/ex8data1.mat')
X = data['X']
# X.shape
fig = plt.figure()
ax1 = fig.add_subplot(111)
ax1.scatter(X[:,0], X[:,1])
# plt.show()
# 该聚类的中心十分紧密，只有几个值远离聚类中心。 在这个简单的例子中，这些可以被认为是异常。 为了弄清楚这些，我们的任务是
# 估计数据中每个特征的高斯分布。 为了定义概率分布，我们需要两个东西——均值和方差。 为了实现这一点，我们将创建一个简单的
# 函数来计算数据集中每个特征的均值和方差。
def estimate_gaussian(X):
    mu = X.mean(axis=0)  # 对X的每一列（每一个特征）计算均值
    sigma = X.var(axis=0)  # 对X的每一列计算方差
    return mu, sigma

mu, sigma = estimate_gaussian(X)
print(mu, sigma)

# 现在有了我们模型的参数，我们需要确定概率阈值，其指示一个样本是否应该被认为是异常。 为此，我们需要使用一组已被标记的验证
# 数据（其中真正的异常已经被标记出来了），并在不同阈值条件下测试模型识别异常的能力。
Xval = data['Xval']    # 验证数据
yval = data['yval']    # 分类的标注（0，1 正常，异常）

# fig,ax = plt.subplots()
# ax.scatter(Xval[:,0], Xval[:,1])

# print(Xval)
# Xval.shape, yval.shape
# 需要一种方法能够在给定参数下计算数据点属于一个正态分布的概率

# print(X[:,0][0:50])
dist = stats.norm(mu[0], sigma[0]) # 第一列的均值和方差
dist.pdf(X[:,0])[0:50]     # X点的概率密度

# za = dist.pdf(X[:,0])

p = np.zeros((X.shape[0], X.shape[1]))
p[:,0] = stats.norm(mu[0], sigma[0]).pdf(X[:,0])   # X第一列的概率密度
p[:,1] = stats.norm(mu[1], sigma[1]).pdf(X[:,1])   # X第二列的概率密度


pval = np.zeros((Xval.shape[0], Xval.shape[1]))
pval[:,0] = stats.norm(mu[0], sigma[0]).pdf(Xval[:,0])   # Xval第一列的概率密度
pval[:,1] = stats.norm(mu[1], sigma[1]).pdf(Xval[:,1])
# print(pval)

# 我们需要一个只要给定概率密度值和真标签就能找出最佳阈值的函数。 为此，我们需要计算不同的 ϵ 值的 F1 范数。 F1 范数是真正
# （ true positive）、假正（false positive）、假负（false negative）的函数。

# print(pval.min(),pval.max())
# 7.51302142773e-15 0.233334292828

# pre = pval < pval.max()
# print((np.logical_and(pre[10,:] == 1, yval == 0)))
# print([True,True]==1)

def select_threshold(pval, yval):   # 验证数据两列的概率密度， 验证数据的标注
    best_epsilon = 0
    best_f1 = 0
    f1 = 0

    step = (pval.max() - pval.min()) / 100

    for epsilon in np.arange(pval.min(), pval.max(), step):   # 等差数列 起始 步长
        preds = pval < epsilon  # 比较结果赋值给preds
        # (307, 2)的比较结果

        tp = np.sum(np.logical_and(preds == 1, yval == 1)).astype(float)   # 逻辑与、类型转换  #真正
        # 计数  统计预测1实际1的数目
        fp = np.sum(np.logical_and(preds == 1, yval == 0)).astype(float)  # 假正
        # 验证数列正常数据中有一点概率密度小于阈值
        fn = np.sum(np.logical_and(preds == 0, yval == 1)).astype(float)  # 假负
        # 验证数列异常数据中有一点概率密度大于阈值

        # 假正指的是这样的一个数据实例：我们创建的这个模型预测它应该是正的，但事实相反，实际值却是负的。同样地，假负指的
        # 是这样一个数据实例：我们创建的这个模型预测它应该是负的，但事实相反，实际值却是正的。
        precision = tp / ((tp + fp)+ 0.0000000001)     # 被模型预测为正的正样本/被模型预测为正的正样本+被模型预测为正的负样本
        recall = tp / (tp + fn)   # 真正例率   正样本预测结果数 / 全部正样本实际数
        # FP /（FP + TN） 假正例率    被预测为正的负样本结果数 /负样本实际数
        f1 = (2 * precision * recall) / ((precision + recall)+0.000000000001)

        if f1 > best_f1:
            best_f1 = f1
            best_epsilon = epsilon
    return best_epsilon, best_f1

epsilon, f1 = select_threshold(pval, yval)
print(epsilon,f1)  # 0.00956670600596 0.714285714283
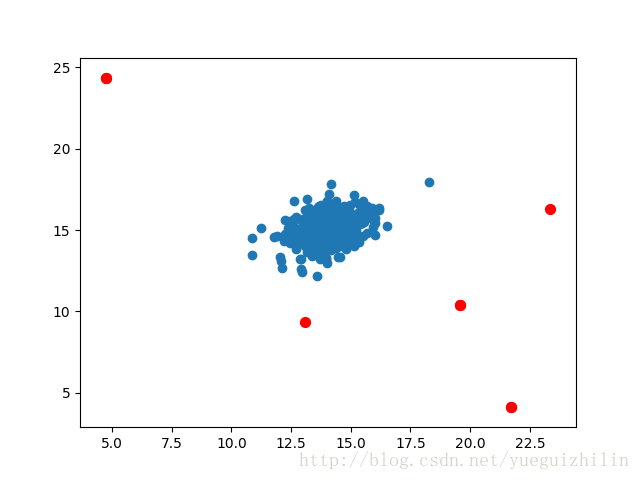
outliers = np.where(p < epsilon)
# outliers = np.where(za<0.04)
# print(outliers)

fig, ax = plt.subplots()
ax.scatter(X[:,0], X[:,1])
ax.scatter(X[outliers[0],0], X[outliers[0],1], s=50, color='r', marker='o')
plt.show()
机器学习练习（四）——异常检测

猜你喜欢
