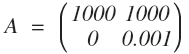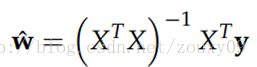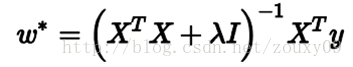在之前的两篇文章岭回归以及L1正则化与L2正则化详解中都有提到L2范数。但对于L2范数在优化计算角度上都跳过了。故在这里新开一篇详细介绍一下,为什么L2范数可以解救病态矩阵,以及优化计算。
病态系统
现在有线性系统: , 解方程
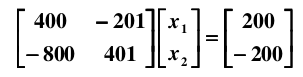
很容易得到解为: 。如果在样本采集时存在一个微小的误差,比如,将 A 矩阵的系数 400 改变成 401:
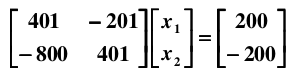
则得到一个截然不同的解: 。
当解集 x 对 A 和 b 的系数高度敏感,那么这样的方程组就是病态的 (ill-conditioned).
经过计算可得
矩阵的条件数(condition number)
如果方阵 A 是奇异的,那么 A 的 condition number 就是正无穷大了。实际上,每一个可逆方阵都存在一个 condition number。
对condition number来个一句话总结:condition number 是一个矩阵(或者它所描述的线性系统)的稳定性或者敏感度的度量,如果一个矩阵的 condition number 在1附近,那么它就是well-conditioned的,如果远大于1,那么它就是 ill-conditioned 的,如果一个系统是 ill-conditioned 的,它的输出结果就不要太相信了(因为这个系统对输入太过敏感了,有时甚至计算机的存储误差对结果都会有显著的影响)。计算公式如下:
计算矩阵的条件数需要知道norm(范数)的定义和Machine Epsilon(机器的精度)。范数就相当于衡量一个矩阵的大小,在L1正则化与L2正则化详解中我们已经介绍了三种范数L0、L1、L2.现在我们介绍一下同样很简单的无穷范数(infinity norm), 即找行绝对值之和最大,举个例子:
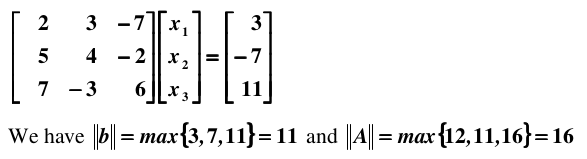
infinity norm 具有三角性质:. 理解了这些概念,下面讨论一下衡量方程组病态程度的条件数,首先假设向量 b 受到扰动,导致解集 x 产生偏差:
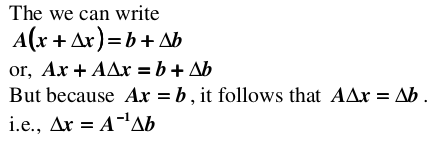
即有:
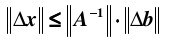
同时,由于
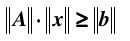
综合上面两个不等式:
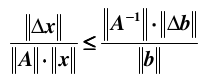
即得到最终的关系:
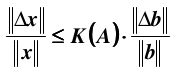
如果是矩阵 A 产生误差,同样可以得到:
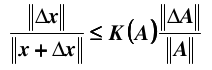
矩阵A产生误差从头到尾再推一遍就能推出来了。
其中, 条件数定义为:
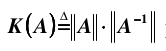
也就是说,当条件数很大的时候,无论是b还是A只要变动一点点就会导致x变动很大。这就是为什么病态系统敏感的原因。
病态的由来
自己的看法:
线性系统 Ax = b 为什么会病态?归根到底是由于 A 矩阵列向量(行向量相关性大应该也有关系)线性相关性过大,表示的特征太过于相似以至于容易混淆所产生的。举个例子, 现有一个两个十分相似的列向量组成的矩阵 A:
在二维空间上,这两个列向量(列向量就是空间中所谓的基向量)夹角非常小。假设第一次检测得到数据 b = [1000, 0]^T, 这个点正好在第一个列向量所在的直线上,解集是 [1, 0]^T。现在再次检测,由于有轻微的误差,得到的检测数据是 b = [1000, 0.001], 这个点正好在第二个列向量所在的直线上,解集是 [0, 1]^T。两次求得到了差别迥异的的解集。
病态矩阵的两大缺点
- 系统太过敏感,无论是略微对A矩阵进行一点改动还是对b矩阵进行一点改动,都会对解x产生较大的影响。此时系统得出的结果通常不可信。
- 如果矩阵是病态矩阵,则在迭代法中,解的收敛非常缓慢。
病态矩阵处理方法
真正的自由是建立在规范的基础上的。病态矩阵解集的不稳定性是由于解集空间包含了自由度过大的方向(就是列向量太多,即基向量太多了,基向量之间并不相互线性无关),解决这个问题的关键就是将这些方向去掉,而保留 scaling 较大的方向,从而把解集局限在一个较小的区域内。
总结起来,解决矩阵病态就是将解集限定在一组正交基空间内。
在机器学习中的矩阵方法(附录A): 病态矩阵与条件数一文中有一个关于SVD分解的例子。有兴趣可以看一下。
L2范数
到这里为止,应该能搞清楚为什么病态矩阵会造成优化求解上的困难了吧。
回到最开始的问题。L2范数有助于处理 condition number不好的情况下矩阵求逆很困难的问题。因为目标函数如果是二次的,对于线性回归来说,那实际上是有解析解的,求导并令导数等于零即可得到最优解为:
然而,如果当我们的样本X的数目比每个样本的维度还要小的时候,矩阵将会不是满秩的,即
,则
会变得不可逆,所以
就没办法直接计算出来了。
所以矩阵
为非满秩矩阵。
或者更确切地说,将会有无穷多个解(因为我们方程组的个数小于未知数的个数)。也就是说,我们的数据不足以确定一个解,如果我们从所有可行解里随机选一个的话,很可能并不是真正好的解,总而言之,我们过拟合了。
怎么突然就扯到过拟合了呢!可以很容易的发现上面的解析表达式实际上是由Normal Equation得出来的结论,在之前的线性回归之Normal Equation一文中,我们介绍过,矩阵A有多少行就表示基向量空间有多少维(每个特征有多少样本量,就表明在这个空间中有多少维度),有多少列,就表示有多少个基向量。这么一个概念,理解起来可能会有些困难,建议回过头去再看一遍Normal Equation方法。
代入到这个情景中,样本X的数目比特征还要小,就是向量空间的维数很低,但是基向量很多。举个例子,就比如在三维空间中,我们却有10个基向量,那当然可以通过这10个基向量进行线性组合,很容易就可以拟合到所有的样本,或者说使得拟合误差极小。这就造成了过拟合!
对于新的样本进来,这种拟合是毫无泛化能力的。
总结一下,病态矩阵的由来在以下两个方面:
- 之前讲的列向量之间相关性过大,此时可能样本量很多,即样本空间的维数很高,空间中的基向量个数(特征数)也不多,但基向量之间(特征之间)的相关性很高。此时就会造成矩阵(特征矩阵)病态。此时的模型应该是欠拟合的,因为大多数的特征提供的信息重复率太高,真正有用的数据分布信息并不多,换一个角度思考,即在样本空间之中,基向量大多指向同一个方向,那个样子拟合能力就很差了,同时作迭代法时想要迭代收敛的速度就很慢(转向特别慢)。
- 第二种病态矩阵就是由于样本数少于特征数,就如上面讲的那样,会造成过拟合!
但如果加上L2正则项,就变成了下面这种情况,就可以直接求逆了:
正如上文所说的:病态矩阵解集的不稳定性是由于解集空间包含了自由度过大的方向,解决这个问题的关键就是将这些方向去掉
自由度太大会造成过拟合泛化能力极差,同时系统又极不稳定。当我们加入正则项之后,A就变成了满秩矩阵,此时矩阵A的样本空间维数和基向量的个数是等量(实际上是大于等于)的,也就是说在5维的向量空间中,我们的特征个数是小于等于5个,即基向量个数是小于等于5个的,此时,拟合出来的函数具有一定的泛化能力。我们通过增大样本的空间维数(实际上没有增大,原先由于线性相关是不满秩的,后来变成了线性独立)使得解集空间的自由度降低了!
文章写的还是有点模糊,以后会继续补充与改善思路。推荐阅读下面两篇参考文献以及结合我的文章与我以前写的一些文章作综合思考。
接下来要补一章内容,关于矩阵的转置乘以矩阵,以及SVD,奇异值特征值等等数学基础知识。
参考文章: