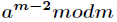同余与模运算

<1> 123456789*987654321 = ()

A: 121932631112635266 B: 121932621112635267

C: 121932631112635268 D: 121932631112635269

解答: 利用公式(ab)mod n = (a mod n)（b mod n）mod n，可以得到

123456789 X 987654321 mod 10 = (123456789 % 10) X (987654321%10) %10 = 9

在这里我们介绍以下三个公式:

(a+b)mod n = ((a mod n)+ (b mod n))mod n;

(a-b) mod n = ((a mod n )- (b mod n)+n)mod n;

ab mod n = (a mod n) (b mod n) mod n

注意，在减法中，由于a mod n 可能小于b mod n，需要在结果上加上n，而在乘法中，需要注意a mod n 和 b mod n相乘考虑是否会溢出，因此这里要注意用long 型保存中间结果。像这样：·

int mul_mod(int a,int b,int n){
    a%=n;
    b%=n;
    return (int )((long long int)a*b%n );
}

2.大整数取模

先把大整数写成“自左向右”的形式：1234 = （（1*10+2）*10+3）*10+4，然后用前面的加法取模公式

（这里用到递归的理解）

scanf("%s%d",n,&m);
int len =streln(n);
int ans=0;
for(int i=0;i<len;i++)
    ans=(int)((long long int )ans*10+n[i]-'0')%m);
printf("%d",ans);

3.幂取模

输入正整数a，n,m，输出a^b mod m 的值。a,n,m<10^9.

(用分治复杂度o(log n) )

int pow_mod(int a,int n,int m){
	if(n==0)	return 1;
	int x=pow_mod(a,n/2,m);
	long long int ans =(long long int )x*x%m;
	if(n%2==1)	ans=ans*a%m;
	return (int )ans;
}

4.模线性方程组

题意：输入正整数a,b,n,解方程ax ≡ b (mod n) a,b,n<=109 。

解答：

a ≡ b(mod n)的意思是说“a 和 b关于模n 同余 ”，即a mod n = b mod n。而a ≡ b mod n 的充要条件是: （a-b）是n 的整数倍。这样，这个问题就变成了ax-b是n的正整数倍。设这个"倍数"是y,则ax - b = ny,即ax - ny= b，因此，这个就回到了解不定方程的问题。

比如给定方程ax +by +c = 0,求出满足这个方程的整数解（x,y）.这里，我们首先来学习扩展欧几里德算法——找出一对整数(x,y)，使得ax+by = gcd(a,b),这里的x,y不一定是整数，也可能是负数或者0，例如gcd(6,15) = 3,6*3 - 15*1 = 3,其中x = 3,y=-1;这个方程还有其他解，比如x = -2,y = 1;以下是一个扩展欧几里德算法的程序：

#include <iostream>  
using namespace std;  
  
int x,y;  
void gcd(int a,int b,int& d,int& x,int& y)  
{  
    if (!b)     { d = a; x = 1; y = 0; }  
    else         { gcd(b,a%b,d,y,x); y -= x*(a/b); }  
}  
int main()  
{  
    int a,b,x,y,d;  
    cin>>a>>b;  
    gcd(a,b,d,x,y);  
    cout<<x<<" "<<y<<endl;  
}

可以证明：设a,b,c为任意整数。若方程ax+by = c 的一组整数解为x0,y0则它的任意整数解都可以写成（x0+kb',y0+ka'），

其中a' =a/gcd(a,b),b' = b/gcd(a,b),k为任意整数。

假设对于ax - ny= b，其中a = 6,n = -15,b = 9，即6x+15y = 9,根据欧几里德算法，我们得到6X(-2)+15X1 = 3,两边同时乘以3，即可得到6X(-6)+15X3 = 9，即x = -6,y = 3是6x+15y = 9的一组解。

最后，还有这样一个结论：设a,b,c为任意整数，g = gcd(a,b),方程ax+by = g的一组解是(x0,y0),则当c是g的倍数时，ax+by=c的一组解是(x0c/g,y0c/g);当c不是g的倍数时无整数解。

5.除法取模（关键求逆元）

逆元：
若，b*b1 % c == 1
则，b1称为b模c的乘法逆元。

在ACM中，许多除法取模都要用到求逆元。
但是，逆元，为什么能给我们带来 ( a/b ) % m == ( a*b1 ) % m？？

（当然a/b要整除）

对于正整数和，如果有，那么把这个同余方程中的最小正整数解叫做模的逆元。

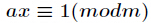
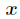
逆元一般用扩展欧几里得算法来求得，如果为素数，那么还可以根据费马小定理得到逆元为。（都要求a和m互质）

猜你喜欢