剑指Offer66题之每日6题 - 第二天

原题链接：

• 第一题：斐波那契数列；
• 第二题：跳台阶；
• 第三题：变态跳台阶；
• 第四题：矩形覆盖；
• 第五题：二进制中1的个数；
• 第六题：数值的整数次方；

第一题：斐波那契数列

题目：

大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项。

n<=39。

解析：

斐波拉契数列的定义：

• $F_0=0, F_1=1$；
• $F_n = F_{n - 1} + F_{n - 2}\quad (n \ge 2)$。

用f1, f2分别表示 $F_{i - 2}$, $F_{i - 1}$，用ret表示$F_i$，每次令ret = f1 + f2,ret就表示$F_{i}$ 得到$F_n$，然后把f1, f2分别更新为$F_{i-1}$, $F_i$, 依次类推，ret的值就是最终$F_n$的值。

int型整数只能保存$F_0 \to F_{46}$，下面是这个区间的斐波拉契数列的值：

0: 0
1: 1
2: 1
3: 2
4: 3
5: 5
6: 8
7: 13
8: 21
9: 34
10: 55
11: 89
12: 144
13: 233
14: 377
15: 610
16: 987
17: 1597
18: 2584
19: 4181
20: 6765
21: 10946
22: 17711
23: 28657
24: 46368
25: 75025
26: 121393
27: 196418
28: 317811
29: 514229
30: 832040
31: 1346269
32: 2178309
33: 3524578
34: 5702887
35: 9227465
36: 14930352
37: 24157817
38: 39088169
39: 63245986
40: 102334155
41: 165580141
42: 267914296
43: 433494437
44: 701408733
45: 1134903170
46: 1836311903

class Solution {
public:
    int Fibonacci(int n) {
        if (n == 0)
            return 0;
        if (n == 1)
            return 1;
        int f1 = 0, f2 = 1, ret;
        for (int i = 2; i <= n; i++)
            ret = f1 + f2, f1 = f2, f2 = ret;
        return ret;
    }
};

第二题：跳台阶

题目：

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

解析：

最简单的动态规划，考虑最后跳上第n阶台阶，有两种方式往上跳：

• 从第n - 1阶往上跳一级到第n阶；
• 从第n - 2阶往上跳二级到第n阶。

那么$f(i)$表示该青蛙跳上一个i级的台阶总共跳法。故$f(i) = f(i - 1) + f(i-2), f(0) = f(1) =1$，这就是变形版的斐波拉契数列啊，直接求解。

class Solution {
public:
    int jumpFloor(int n) {
        if (n == 1)
            return 1;
        int f1 = 1, f2 = 1, ret;
        for (int i = 2; i <= n; i++)
            ret = f1 + f2, f1 = f2, f2 = ret;
        return ret;
    }
};

第三题：变态跳台阶

题目：

一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

解析：

根据上题可以写出下面的公式：

$$f(n)=f(0) + f(1)+\cdots + f(n-1), f(0) = 1$$
开一个数组 f来存储 $f(i)$，二重循环可以得到 $f(i)$；

但是如果你注意到$f(0) + f(1)+\cdots + f(n-2)=f(n-1)$，那么$f(n)$中的$f(0) + f(1)+\cdots + f(n-2)$用$f(n-1)$代替，可以得到下面式子：

$$f(n)=2f(n-1)$$
这是一个首项为 1，公比为 2的等比数列啊，直接可以得到最终表达式 $$f(n)=2^{n-1}$$

class Solution {
public:
    int jumpFloorII(int number) {
        return 1 << (number - 1);
    }
};

第四题：矩形覆盖

题目：

我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

解析：

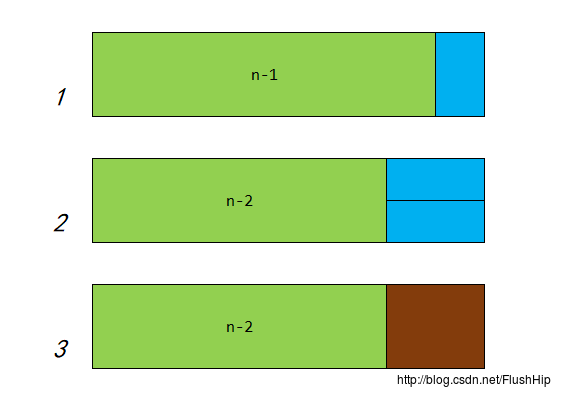
和跳台阶那题一样的思考方式，考虑最后是怎么填充到2*n的矩形的，看下图的1，2：

根据这幅图片我们也可以轻松得到表达式

$$f(n) =f(n-1)+f(n-2),\qquad f(1)=1, f(2)=2$$

千万不要2 中的那两个方块竖直过来再算一种情况，这样会多算，因为这种情况在1中就计算过了，如果题目改一下：用2*1和2*2的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法，那么就要用到3中的情况，那么表达式也要相应改为：

$$f^{'}(n) =f^{'}(n-1)+2f^{'}(n-2),\qquad f^{'}(1)=1, f^{'}(2)=3$$

class Solution {
public:
    int rectCover(int number) {
        if (number == 0)
            return 0;
        if (number == 1)
            return 1;
        if (number == 2)
            return 2;
        int f1 = 1, f2 = 2, ret;
        for (int i = 3; i <= number; i++)
            ret = f1 + f2, f1 = f2, f2 = ret;
        return ret;
    }
};

第五题：二进制中1的个数

题目：

输入一个整数，输出该数二进制表示中1的个数。其中负数用补码表示。

解析：

这题有很多做法，我选一个时间复杂度与该整数二进制代码中1的个数正相关的算法来讲；

首先，你必须知道如何消除二进制中最后一个位1，利用n &= (n - 1)就可以做到。然后看一下消了几次n变成0，次数就是答案。

n &= (n - 1)具体的操作是把最后一位1变成0，后面的0变成1，与运算一下，最后一位1就消掉了。

class Solution {
public:
     int  NumberOf1(int n) {
         int ret = 0;
         for (; n; n &= (n - 1), ret++);
         return ret;
     }
};

要注意，这题是不能用移位来求1的个数的，因为负数用补码表示，而移位是算术移位，如果是负数移位后会在最高位补1，那么就不能正确统计个数，而且程序会死循环，解决方法是把负数强制转换为unsigned int，然后在执行移位，可以得到正确答案。

第六题：数值的整数次方

题目：

给定一个double类型的浮点数base和int类型的整数exponent。求base的exponent次方。

解析：

二分求解，$base^{exp}=(base ^{\frac{exp}{2}})^2*(base\quad or\quad 1)$。

求解的时候判断下exp的正负和exp的奇偶就行了。

时间复杂度：$O(logn)$ 。

class Solution {
public:
    double Power(double base, int exponent) {
        bool f = exponent < 0;
        if ((exponent = abs(exponent)) == 0)
            return 1.0;
        double ret = Power(base, exponent / 2);
        ret = exponent % 2 ? ret * ret * base : ret * ret;
        return f ? 1.0 / ret : ret;
    }
};