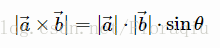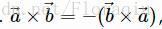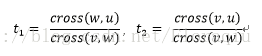计算几何知识归纳

计算几何知识归纳

---

目录

㈠ 点的基本运算
1. 平面上两点之间距离
2. 判断两点是否重合
3. 矢量叉乘
4. 矢量点乘
5. 判断点是否在线段上
6. 求一点饶某点旋转后的坐标
7. 求矢量夹角

㈡ 线段及直线的基本运算
1. 点与线段的关系
2. 求点到线段所在直线垂线的垂足
3. 点到线段的最近点
4. 点到线段所在直线的距离
5. 点到折线集的最近距离
6. 判断圆是否在多边形内
7. 求矢量夹角余弦
8. 求线段之间的夹角
9. 判断线段是否相交
10. 判断线段是否相交但不交在端点处
11. 求线段所在直线的方程
12. 求直线的斜率
13. 求直线的倾斜角
14. 求点关于某直线的对称点
15. 判断两条直线是否相交及求直线交点
16. 判断线段是否相交，如果相交返回交点

㈢ 多边形常用算法模块
1. 判断多边形是否简单多边形
2. 检查多边形顶点的凸凹性
3. 判断多边形是否凸多边形
4. 求多边形面积
5. 判断多边形顶点的排列方向，方法一
6. 判断多边形顶点的排列方向，方法二
7. 射线法判断点是否在多边形内
8. 判断点是否在凸多边形内
9. 寻找点集的graham算法
10. 寻找点集凸包的卷包裹法
11. 判断线段是否在多边形内
12. 求简单多边形的重心
13. 求凸多边形的重心
14. 求肯定在给定多边形内的一个点
15. 求从多边形外一点出发到该多边形的切线
16. 判断多边形的核是否存在

㈣ 圆的基本运算
1. 点是否在圆内
2. 求不共线的三点所确定的圆

㈤ 矩形的基本运算
1. 已知矩形三点坐标，求第4点坐标

㈥ 常用算法的描述

㈦ 补充
1. 两圆关系
2. 判断圆是否在矩形内
3. 点到平面的距离：
4. 点是否在直线同侧：
5. 镜面反射线：
6. 矩形包含：
7. 两圆交点：
8. 两圆公共面积：
9. 圆和直线关系：
10. 内切圆：
11. 求切点：
12. 线段的左右旋：
13. 公式：

---

点和向量
1、点和向量定义

在平面坐标系下，向量和点一样，均用两个数x,y表示。

struct Point 
{
    double x, y;
    Point(double a = 0, double b = 0):x(a), y(b){}
};

typedef Point Vector;//从程序实现上来说，向量是点的别名

2、向量加减、数乘

• 向量 + 向量 = 向量 点 + 向量 = 点

Vector operator + (Vector A, Vector B)
{
    return Vector(A.x + B.x, A.y + B.y);
}

• 点 - 点 = 向量

Vector operator - (Vector A, Vector B)
{
    return Vector(A.x - B.x, A.y - B.y);
}

• 向量 * 数 = 向量

Vector operator * (Vector A, double p)
{
    return Vector(A.x * p, A.y * p);
}

• 向量 / 数 = 向量

Vector operator / (Vector A, double p)
{
    return Vector(A.x / p, A.y / p);
}

• 两点的欧氏距离

double dist(Point A, Point B)
{
    return sqrt( (A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y));
}

3、 判断两个点是否重合及先后顺序

bool operator < (const Point & a, const Point & b)
{
    return a.x < b.x || (a.x == b.x && a.y < b.y);
}

const double EPS = 1e-10;
int dcmp(double x)//三态函数，处理与double零有关的精度问题
{
    if(fabs(x) < EPS)
        return 0;
    else
        return x < 0 ? -1 : 1;
}

bool operator = (const Point & a, const Point & b)
{
    return dcmp(a.x - b.x) == 0 && dcmp(a.y - b.y) == 0;
}

4、向量极角

极角，即从x轴正半轴旋转到该向量方向所需要的角度。
直接调用库函数float atan2(float x, float y)即可计算极角（单位：弧度）

5、向量点积

• 向量v, w的点积 = |v| * |w| * cos θ = Xa * Xb + Ya * Yb
• θ 是指从v到w逆时针旋转的角度，当 θ > 90°时，点积为负， θ = 90°时，点积为0，当 θ < 90°时，点积为正。
• 点积满足交换律

• 点积的几何意义是v在w的投影v’与w的长度乘积

  

• 点积

double Dot(Vector A, Vector B)
{
    return A.x * B.x + A.y * B.y;
}

• 向量长度

double Length(Vector A)
{
    return sqrt(Dot(A, A));
}

• 向量夹角

double Angle(Vector A, Vector B)
{
    return acos(Dot(A, B) / Length(A) / Length(B));
}

6、向量叉积

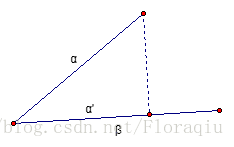
• 向量a 和b 叉积, 得到一个垂直于a 和b 的向量a ×b , 它的方向由右手螺旋法则确定, 它的长度是a 和b 张开的平行四边形的面积
  
  其中θ是a和b的夹角.
  
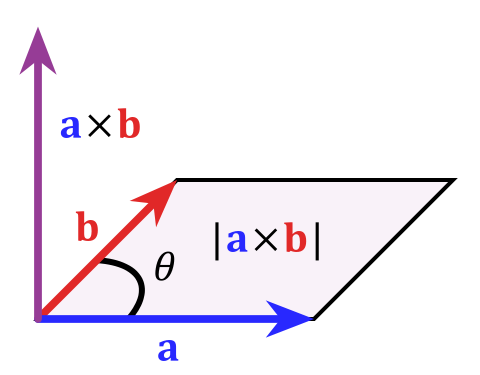
• 右手螺旋法则 ：四指由a开始，指向b，拇指的指向就是a×b的方向，垂直于a和b所在的平面。
• 顺着第一个向量a看，如果b在左边，那么他们的叉积大于0，否则小于0，如果共线，则为0。
• 向量OA和向量OB 的叉积 = Xa * Y b - Xb * Ya
• 叉积不满足交换律，

• 叉积的几何意义是α和β所张成的平行四边形的有向面积
  

• 叉积

double Cross(Vector A, Vector B)
{
    return A.x * B.y - A.y * B.x;
}

• 三点构成的四边形面积

double Area2(Point A, Point B, Point C)
{
    return Cross(B - A, C - A);
}

7、向量旋转

• 向量绕起点旋转，∠α为逆时针旋转的角
  x' = x * cosα - y * sinα
y' = x * sinα + y * cosα
• 向量旋转

Vector Rotate(Vector A, double rad)//rad为弧度
{
    return Vector(A.x * cos(rad) - A.y * sin(rad), A.x * sin(rad) + A.y * cos(rad));
}

8、向量的单位法线

单位法线即旋转90度后，把长度归一化

//调用前确保A不是零向量
Vector Normal(Vector A)
{
    double L = Length(A);
    return Vector(-A.y / L, A.x / L);
}

---

直线、射线、线段

1、线的表示方法

• 线可以用直线上一点P0和方向向量v表示
  
  • 线上所有点P满足 P = P0 + t * v
  • 如果已知直线上两个不同的点A和B，则方向向量为B - A
  • 直线：t无限制
  • 射线：t > 0
  • 线段：t在0~1之间

2、直线交点

• 设直线分别为 P + t * v 和 Q + t * w
  设向量 u = P - Q
  设交点在第一条直线的参数为t1，在第二条直线的参数为t2
  则

• 两直线有唯一交点，当且仅当Cross(v,w) != 0

// 调用函数前确保有唯一交点
Point GetLineIntersection(Point P, Vector v, Point Q, Vector w)
{
    Vector u = P - Q;
    double t = Cross(w, u) / Cross(v, w);
    return P + v * t;
}

3、点到直线的距离

• 点到直线的距离 = 平行四边形面积（叉积） / 底
• 如果不取绝对值，则得到有向距离

double DistanceToLine(Point P, Point A, Point B)
{
    Vector v1 = B - A, v2 = P - A;
    return fabs( Cross(v1, v2) / Length(v1));
}

4、点到线段的距离

设投影点为Q

• 如果Q在AB上，则所求为P到直线AB距离
• 如果Q在A的左边，则所求为AP长度
• 如果Q在B的右边，则所求为BP长度

double DistanceToSegment(Point P, Point A, Point B)
{
    if(A == B)
        return Length(P - A);
    Vector v1 = B - A, v2 = P - A, v3 = P - B;
    if(dcmp( Dot(v1, v2) ) < 0)
        return Length(v2);
    else if(dcmp( Dot(v1, v3) > 0))
        return Length(v3);
    else
        return fabs( Cross(v1, v2) / Length(v1));
}

5、点在直线上的投影

• 设点P在直线AB上的投影为Q，（直线为A + t * v， v = 向量AB），Q的参数为t0，Q= A+ t0 * v，根据PQ垂直于AB，向量点积为0，则Dot（v,P - （A + t0 * v）) = 0，根据分配率，Dot（v，P - A）- t0 * Dot（v，v）= 0。

Point GetLineProjection(Point P, Point A, Point B)
{
    Vector v = B - A;
    return A + v * ( Dot(v, P - A) / Dot(v, v));
}

6、点在线段上【不包含端点】

double OnSegment(Point p, Point a1, Point a2)
{
    return dcmp( Cross(a1 - p, a2 - p) ) == 0 && dcmp( Dot(a1 - p, a2 - p) ) < 0;//前者保证p在该直线上，后者保证p在AB中间，即在线段上
}

7、线段相交判定

• 规范相交
  
  • 定义：两线段恰好有一个公共点，且不在任何一条线段的端点。
  • 充要条件：每条线段的两个端点都在另外一条线段的两侧。（“两侧”指叉积符号不同）

bool SegmentProperIntersection(Point a1, Point a2, Point b1, Point b2)
{
    double c1 = Cross(a2 - a1, b1 - a1),
           c2 = Cross(a2 - a1, b2 - a1),
           c3 = Cross(b2 - b1, a1 - b1), 
           c4 = Cross(b2 - b1, a2 - b1);
    return dcmp(c1) * dcmp(c2) < 0 && dcmp(c3) * dcmp(c4) < 0;
}

• 如果允许在端点相交：
  
  • 如果c1 == c2 == 0，表示两线段共线，可能会有部分重叠的情况
  • 如果c1 和 c2不都为0，则某个端点在另外一条线段上。

---

多边形

1、多边形面积

• 可以将多边形划分为多个三角形，因为三角形面积是有向的，在多边形外面的部分会正负抵消。
• 可以从任意点划分，但最好从p[0]开始划分，这样可以少算两个叉积（0和任意向量的叉积都为0），减少乘法溢出的可能，还不用特殊处理（i = n - 1时，下一个顶点为p[0]，而不是p[n]，因为p[n]不存在）。

double PolygonArea(Point * p, int n)
{
    double area;
    for(int i = 1; i < n - 1; i++)
    {
        area += Cross(p[i] - p[0], p[i + 1] - p[0]);
    }
    return area / 2;//因为前面都计算的是四边形的面积。
}

2、点在多边形内判定

• 射线法：判断穿越数，从某个判定点出发，任意引一条射线，如果和边界相交奇数次，说明点在多边形内；如果相交偶数次，说明点在多边形外。射线如果在端点处和多边形相交，或者穿过一条完整的边，则需要重新引一条射线。

int isPointInPolygon(Point p, Polygon poly)
{
    int wn = 0;
    int n = v.size();
    for(int i = 0; i < n; i++)
    {
        if(isPointOnSegment(p, poly[i], poly[(i + 1) % n]))//在边界上
            return -1;
        int k = dcmp(Cross(poly[(i + 1) % n] - poly[i], p - poly[i]));
        int d1 = dcmp(poly[i].y - p.y);
        int d2 = dcmp(poly[(i + 1) % n].y - p.y);
        if(k > 0 && d1 <= 0 && d2 > 0)
            wn++;
        if(k < 0 && d2 <= 0 && d1 > 0)
            wn--;
    }
    if(wn != 0)
        return 1;//内部
    return 0;//外部
}

• 转角法，看多边形相对于这个点转了多少度，如果转角和 = 360°，说明在多边形内，如果 - 0°，说明在多边形外，如果 = 180°，说明在边界上。

• 二分法：

  • 选择多边形其中一个点为起点，连接其它点作射线。
    
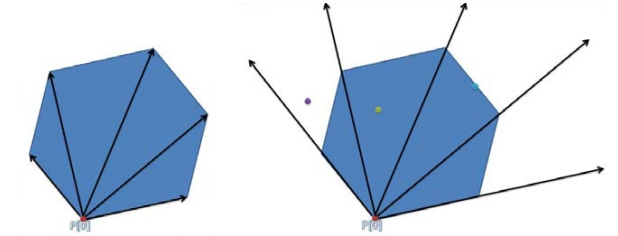
  • 判断给定的点是否在所有射线包围的区域之内，即判断给定点是否在最左侧射线的左边，或者在最右侧射线的右边。
  • 如果在射线包围的区域之内，选择构成最两侧的射线的点为left和right，则mid = (left+right)/2，连接给定点和起点作射线，判断该射线在mid点和起点的哪一边，不断循环，如此用二分法最后求出给定点所在的三角形区域。
    
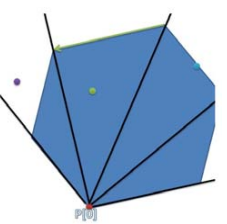
  • 连接left 和 right 点，判断给定点在这条边的左方还是右方，由此判断给定点是否在三角形区域内，也就是是否在多边形内。

int isPointInPolygon(Point p, polygon poly)
{
    if( dcmp(Area2(poly[0], poly[1], p)) <= 0 || dcmp(Area2(poly[0], poly[n - 1], p)) >= 0) ///在最左射线或最右射线的外面，或者恰好在这两射线的边上
        return -1;//外部
    int l = 1, r = n - 1;
    while(r - l > 1)
    {
        int mid = (r - l) / 2 + l;
        if(dcmp(Area2(poly[0], poly[mid], p)) > 0)//p在该射线的左边
            l = mid;
        else
            r = mid;
    }
    if(dcmp(Area2(poly[l], poly[r], p)) <= 0)//p在该射线的右边，即在三角形上面
        return -1;//外部
    return 1;//内部
}