数论之费马小定理

费马小定理：

假如p是素数，且(a,p)=1(a,p)=1,那么a^(p-1)≡1(mod p)

ps:a≡b(modm)表示a,b对模m的余数相同,如3三5(mod2)等

证明略

注意：

1、费马小定理只能在 gcd(a,p)=1 条件成立时使用

2、费马定理是，已知素数p，得到 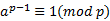。但是已知 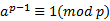 并不能确定p是素数。

3、 若  ，则p一定为合数（费马定理的逆反命题）。

费马小定理在acm中的应用：

① 判断素数，对于大素数的判定，Miller-Rabin 素数判定 
②求解逆元 ，设a模p的逆元为x，则a*x≡1(mod p) ,(a,p)=1;由费马小定理可以知道x=a^(p-2) 
③对于计算a^b(modp)    a^b(modp) 可简化 
            对于素数p，任取跟他互素的数a，有a^(p-1)(mod p)=1 
            所以任取b，有a^b%p=a^(b%(p-1))(%p)从而简化运算。 

①、判断素数模板（利用(a^p-1)%p是否等于1 来判断 是不是素数）

#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <cstdio>
#include <ctime>
#include <cmath>
using namespace std;
#define ll long long
//求a^p%mod
ll quick_pow(ll a,ll p,ll mod)
{
    ll ans=1;
    a=a%mod;
    while(p)
    {
        if(p&1)
            ans=ans*a%mod;
        a=a*a%mod;
        p>>=1;
    }return ans;
}
/*
测试 n 是否为素数 s 为 测试次数 (一般为4次)
是素数 返回 1 不是素数 返回 0
*/
int Miller_Rabbin(ll n,int s)
{
    ll a;
    srand(time(NULL));
    for(int i=1;i<=s;i++)
    {
        a=1+rand()%(n-1);
        if(quick_pow(a,n-1,n)!=1)
            return 0;
    }return 1;
}
int main()
{
    ll n;
    while(cin>>n)//"n=1 的时候特判一下"
    {
        if(n==1) cout<<"   不是素数"<<endl;
        else
        if(Miller_Rabbin(n,4))
            cout<<"   是素数"<<endl;
        else cout<<"   不是素数"<<endl;
    }return 0;
}
/*
1
   不是素数
23
   是素数
2
   是素数
3
   是素数
4
   不是素数
5
   是素数
6
   不是素数

*/

 ②求解逆元

逆元类似导数的性质 （为什么不是相等呢？搞不懂 (╥╯^╰╥) 迷之数论）

接下来引入求余概念

(a +  b) % p = (a%p +  b%p) %p  （对）

(a  -  b) % p = (a%p  -  b%p) %p  （对）

(a  *  b) % p = (a%p *  b%p) %p  （对）

(a  /  b) % p = (a%p  /  b%p) %p  （错）--> 除法是不能直接取模的哦 反例：(100/50)%20 = 2  ≠  (100%20) / (50%20) %20 = 0

所以就要借助逆元了，来把除法转化成乘法；

a的逆元，我们用inv(a)来表示

那么-------------------->>>

(a  /  b) % p = (a * inv(b) ) % p = (a % p * inv(b) % p) % p  （ p 是质数且 gcd(a, p) = 1，a才有关于p的逆元）

 利用费马小定理：a^(p-1)≡1(mod p)   -->   a^(p-2)≡1/a(mod p)   -->   a^(p-2)≡ inv(a) (mod p);

所以 ： inv（a）= a^(p-2)(mod p) ; 

利用快速幂求，

#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <cstdio>
#include <ctime>
#include <cmath>
using namespace std;
#define ll long long
ll quick_pow(ll a,ll b,ll mod)
{
    ll ans=1;
    while(b)
    {
        if(b&1)
            ans=ans*a%mod;
        a=a*a%mod;
        b>>=1;
    }
    return ans;
}
ll Fermat(ll a,ll p) //a 关于 p的逆元
{
    return quick_pow(a,p-2,p);
}
int main()
{
    ll a,p;
    double ans=0;
    cin>>a>>p;
    ans=Fermat(a,p);
    cout<<ans<<endl;
    return 0;
}

③简化计算。还是利用快速幂

快速幂不懂得 戳->https://mp.csdn.net/postedit/79393296