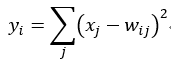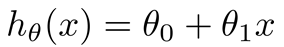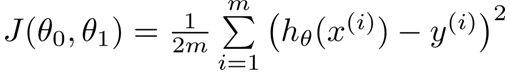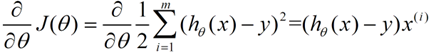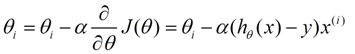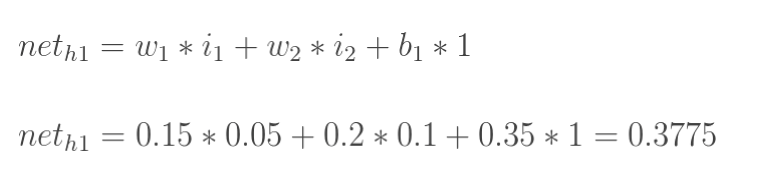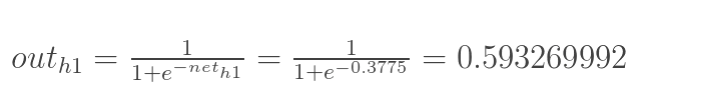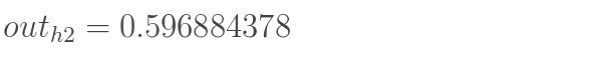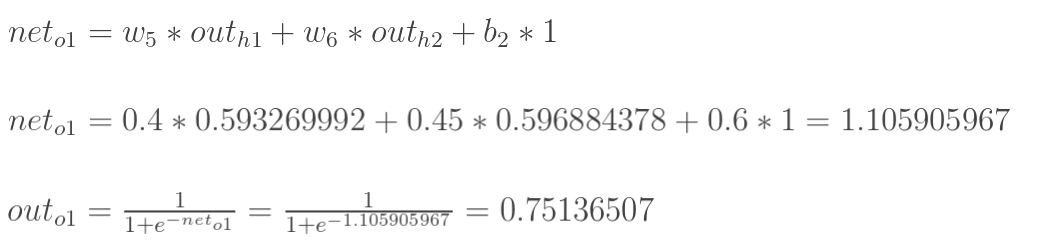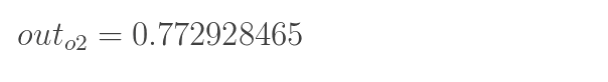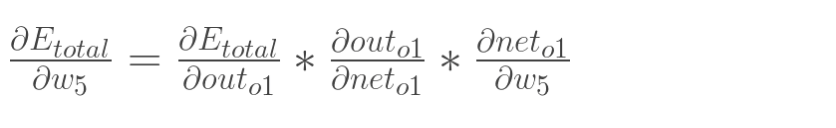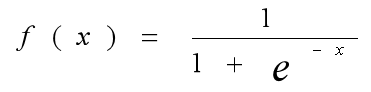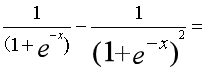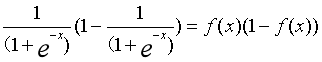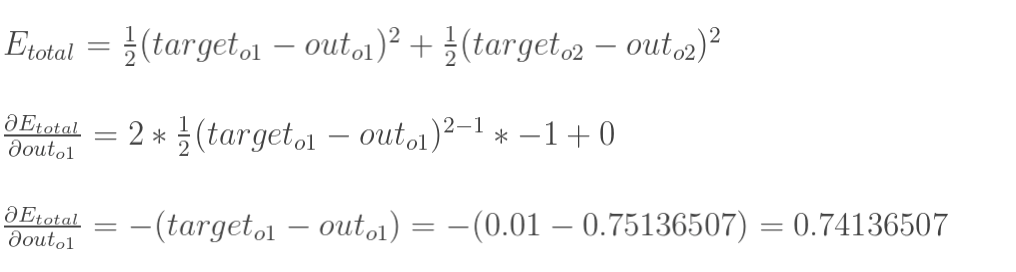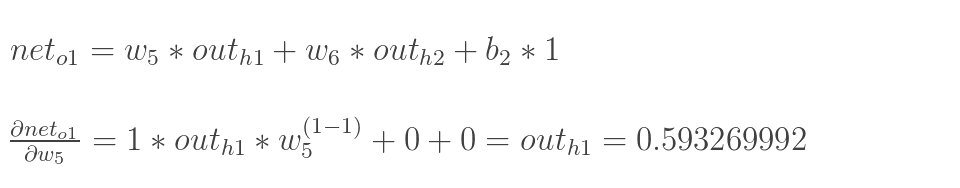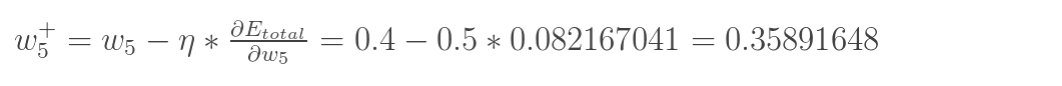学习卷积神经网络,最好的办法就是去实现一些著名的模型:LeNet,AlexNet,ZF-Net,GoogleNet,VGG,ResNet。首先是最老的最简单的LeNet:
先上张图:
这张图就已经将LeNet模型的基本内容与操作描述出来了:卷积-池化-卷积-池化-全连接,除了池化层与最后一层全连接层不用激活函数,其他层都要用.先要说明:需要激励函数Sigmoid解决非线性问题从而将把激活的神经元特征通过函数把特征保留并映射出来,否则无论有多少层得出的结果依然是线性的函数。现在来一层层分析。
C1卷积层:
在这层,卷积核是5x5的二维的,所以得出的特征图是(32-5+1)28*28规格的,因为使有6个卷积核,所以会有6张特征图(这里不再赘述具体卷积的过程,但要注意每一次卷积后都要加上一个偏置值)。特别的,这层的可训练参数有:(5*5+1)*6=156;因为每个卷积核上的每一个元素都是权重值(5*5=25个),在加上一个偏置数bias,那么一个卷积核就有(5*5+1)=26个,6个卷积核有26×6=156个可训练参数。而连接数的计算为:156×28×28×6=122304,就是输出的特征图的每个神经元都与156个参数链接。
S2池化层:
那么这里的采样方法是:用2*2的采样区间,4个元素相加后乘以一个可训练参数再加上一个偏置数,最后再用Sigmoid激活函数非线性化。输出的特征图有6张14*14的(28/2=14)。这层的可训练参数有:(1+1)*6,连接数计算为:(2*2+1)*14*14*6。有些人可能会看出池化层的连接数与卷积层计算有些不同,我也不是很理解,但是可以知道形式:(采样区元素个数+1个偏置)*输出的x张特征图神经元总数。
C3卷积层:
在这层,卷积的操作就不是像C1层那样简单。上图:
如图,输入有6张14*14图,输出有16张10*10图,所以有16个5*5卷积核。这里是将几张输入的图组成一个组合,如取三张相邻的输入为一组(注意这里的相邻的意义):012,123,234,345,451,501有这6组,然后取四张相邻的输入为一组:0123,1234,2345,3450,4501,5012有6组,然后取四张不相邻的输入成一组:0134,1245,0235有三组,最后将6张输入成一组:012345。这样我们就有了6+6+3+1=16这样的4大组16小组,每个卷积核处理一个小组生成一张输出的10*10的特征图。这样做的理由是控制参数个数并打破对称性,期望学得互补的特征。那么问题又来了:3/4/6张输入分别与一个卷积核要如何才能输出一张图?答案很简单:一个卷积核与3/4/6生成3/4/6张图,将3/4/6张图加起来就是所要的特征图。可训练参数:(5*5*3+1)*6+(5*5*4+1)*6+(5*5*4+1)*3+(5*5*6+1)*1=1516;这里需注意:将卷积核想成三维的就好理解为什么是5*5*3了,连接数:(5*5*3+1)*10*10*6+(5*5*4+1)*10*10*6+(5*5*4+1)*10*10*3+(5*5*6+1)*10*10*1=10*10*1516=151600。
S4池化层:
在这层,16张10*10输入图,输出16张5*5特征图,所以采样区大小为2*2。同理,可训练参数:(1+1)*16,
连接数:(2*2+1)*5*5*16。
C5全连接层:
在这层,16张5*5图,输出为120张1*1的图,所以卷积核有120个规格为5*5*16的。那么可训练参数:(5*5*16+1)*120=48120;连接数:(5*5*16+1)*1*1*120=48120。
F6全连接层:
如字面意思,全连接层就是将输入的x张图的每一张图化成一个数值,最后组成一个一维的矩阵,这样就将输入连接起来了。在具体的操做层面,全连接就是卷积。120张1*1的输入,84张1*1的输出,卷积核选择与输入相同规格1*1有84张,卷积一次得出一个数值再加上一个偏置。所以可训练参数有:(1*1*120+1)*84=10164,连接数:(1*1*120+1)*84*1=10164。
OUTPUT层:
这层也称为高斯连接,由欧式径向基单元组成,每一个分类为一个单元,函数如下:
其中X代表输入,而Y代表函数的输出。那么在这里,共有10个分类,那么就有10个y,每一个y都有84个输入x。同样是全连接层,选择的10*84的权重矩阵,w就是每个输入对应的权重参数。得出y后在放入Sigmoid激活函数中产生一个i单元,最后10个单元都算出来,最后用softmax+argmax解决分类问题。
这里在再记录梯度下降法:
举一个简单的例子:需要拟合一个一次函数:
假设正确结果是y,那么就会有误差,我们给出误差函数:
因为J函数中的x和y就是给出的样本,每次求J时都一样,所以J就变成了西塔0和西塔1的函数。那么这时问题就是:如何求出当J取min值时两个西塔的值?解决方法之一就是梯度下降法。
首先,J是一个多元函数,对J的求其中一个元的偏导数,就是求出这个元的在函数上每个点的导数,就可以得到这个元在某个点是否为递增或递减,从而决定这个元的更新方向。a是学习率,决定下降的步子大小,即快慢。
所以梯度下降为:先将样本放到每一个x和y上,在开始的时候分别给两个西塔一个初始值,然后不断更新两个西塔的值直到J函数的值收敛,得到的J就是近似的最小值,得到的两个西塔就是所要参数,把参数带回h函数,那么此时这个函数的拟合效果就是最好的。需要特别注意的是:假设J有n个参数,在更新参数时,你需要同步更新这些参数,不能更新一个就带入一个,这是不对的,会影响求导的结果。
但是在神经网络中如何使用梯度下降法呢?所用到的就是传播算法与反向传播算法。
1.正向传播
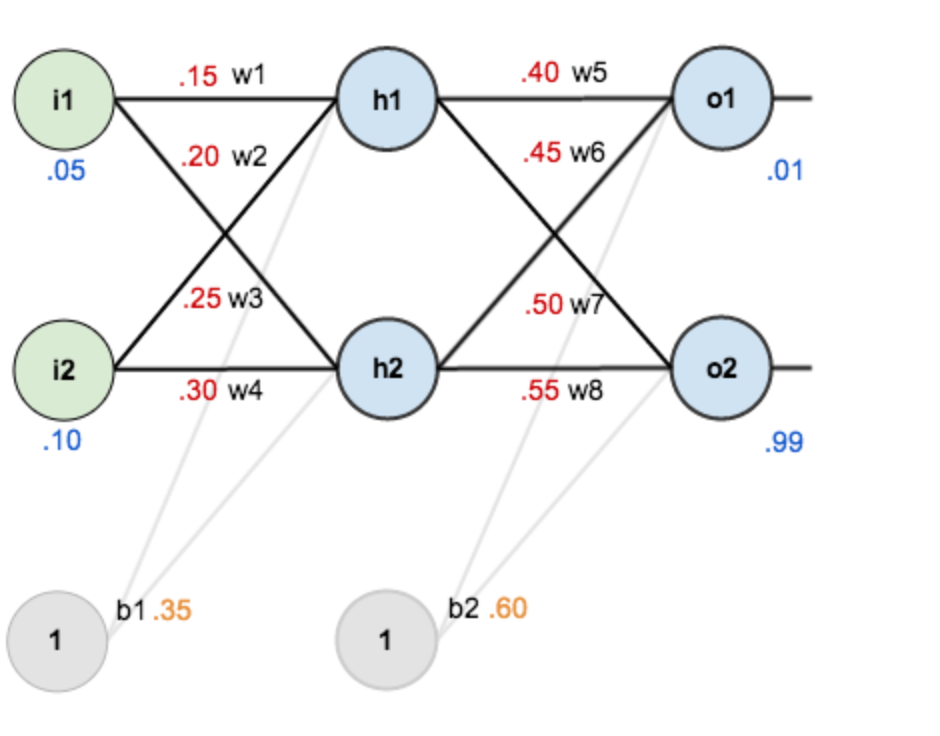
这是一个简单的三层神经网络,w是权重参数,b是偏置值。我们给w和b初始值:
所以现在给出输入i1=0.05,i2=0.10,让输出的o1和o2的值尽可能接近0.01和0.99.
向前传播:
计算h1的加权和:
然后计算h1输给o1的值(就是用Sigmoid函数处理一下):
同理可求
然后计算输出层的o1和o2:
同理:
这样拟合的结果是[0.75136507,0.772928465],显然距离正确结果还挺远。所以要用反向传播法来更新参数。
2.反向传播
首先实现隐含层->输出层的参数的更新(即更新w5,6,7,8)
首先,总误差是: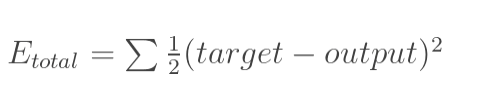
用更新w5作为例子:
同样的,用总误差对w5求偏导数,但是不能直接求,这里需要使用用链式法则。
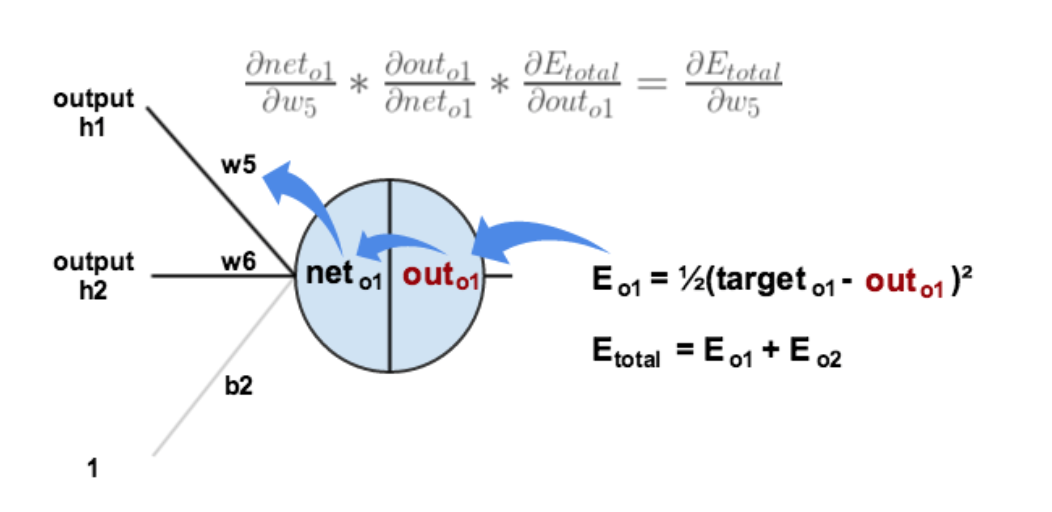
从上面的图就可以知道,总误差先传给Outo1,再给neto1,最后传给w5.所以有:
在处理之前先要知道Sigmoid函数的求导:
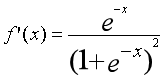
下面分别计算式子中三个偏导:
最后乘起来:
就求出了对w5的偏导,接着就可以更新w5:
n为学习率,同理:
接着实现隐藏层->隐藏层的参数更新(即更新w1,2,3,4).
如上图,总误差直接传给Outh1,再给neth1,最后到w1中。
就能够更新w1,2,3,4了。但要注意,8个w都是同步更新的,分开写只是便于理解。
这样重复下去,总误差就会变的很小,拟合值就会极限接近正解。