虚树一开始听的时候觉得很高深,其实也是一个比较容易的东西。
可以称它是个数据结构,也可以称它是个算法,反正比较好用啦~
定义
虚树就是将原树中的点集 \(S\) 拿出来,构成一棵新的并能保持原树结构的一棵树。
保持结构,意味着对于 \(\forall x, y \in S\) ,他们的最近公共祖先 \(lca\) 也得出现在虚树中来。
举个栗子:
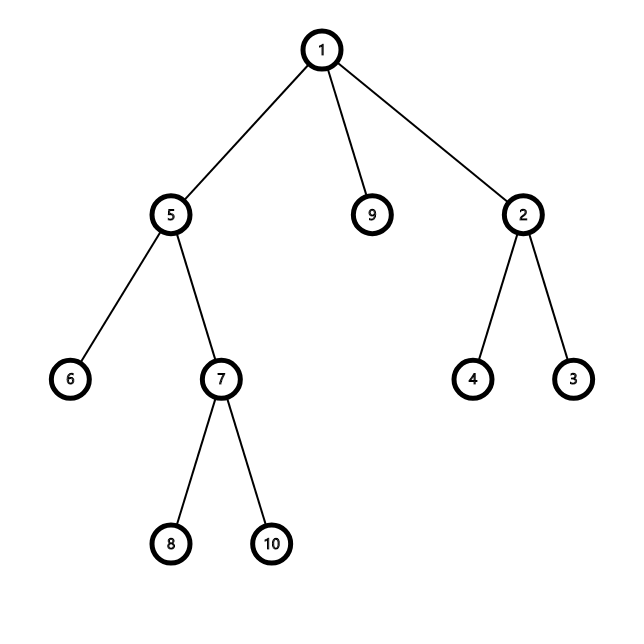
对于这颗树来说
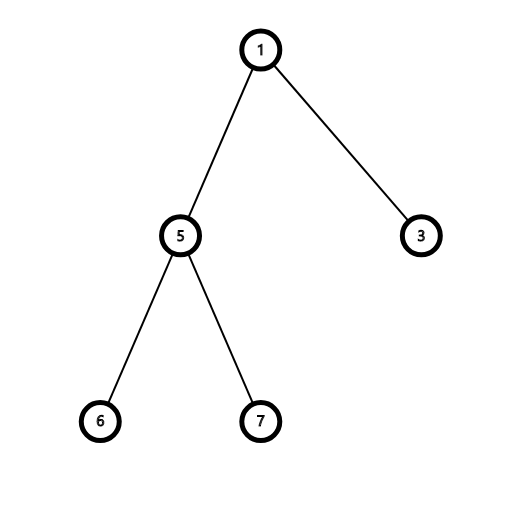
我们将 \(\{3, 6, 7\}\) 取出来变成一棵虚树就是这样的:
我们保留了这些点的 \(lca\) 以及它本身,然后根据他们在原树中的相对关系建了出来。
所有点对的 \(lca\) 个数是严格 \(< |S|\) 的,后面能利用构造的方式进行证明。
构建
首先我们讲所有可能出现的点拿出来,也就是 \(S\) 集合中点对的 \(lca\) ,以及 \(S\) 本身,我们称这些点为关键点,他们构成了一个集合 \(T\) 。
我们将所有点按照他们的 \(dfs\) 序进行排序,然后相邻两个求 \(lca\) 就是所有点对的 \(lca\) 了。
不知道 \(dfs\) 序能看看我 这篇博客 。
接下来我们证明一下为什么这样就是对的。
证明:
如果有点对 \((x, y)\) 排序后不是相邻点对,他们的 \(lca\) 必然出现在别的里面。
如图所示
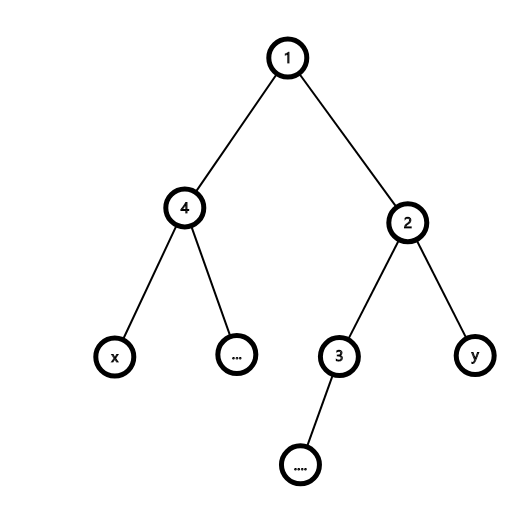
\(x, y\) 的 \(lca\) 为 \(1\) ,那么选择一个 \(dfs\) 序最大且在 \(dfs\) 序在 \(x\) 后面的 \(4\) 的子树的点 \(a\),
不难发现 \(a\) 的 \(dfs\) 序下一个点只能存在与 \(2\) 的子树当中,而这一对的 \(lca\) 为 \(1\) ,就已经包括了 \(x, y\) 的 \(lca\) 。
同理,就算不存在 \(a\) ,我们用 \(x\) 来替代 \(a\) 也能达到相同的效果。
其他情况全都可以类比论证,那么证毕。
怎么觉得证得很伪啊然后将这些点再按 \(dfs\) 序排序,然后用
std :: unqiue去重。用一个栈维护一条从根下来的关键点链,然后不断对于这个栈进行操作,每次将新加进来的点与栈顶连一条边。
因为是按照 \(dfs\) 序进行排序,所以一条链上的点是按照从高到低一个个出现的。
- 每次假设进来一个点 \(x\) ,我们把这个点与栈顶进行比较,如果 \(x\) 在栈顶点的子树中,连一条边我们就可以直接入栈。
- 否则我们一直弹掉栈顶元素,直至满足上面的要求(或者栈为空)
判断是否在子树中,我们可以记一下这个点进来的时间戳(也就是他的 \(dfs\) 序)
pre[u]以及离开的时间戳post[u]如果这个post[u] >= pre[v],那么意味着 \(v\) 在 \(u\) 的子树中。(因为有按pre排序的前提)这个过程可以形象地理解成有一条链从左往右不断在晃,然后每个点只需要连上他在这条链的父亲就行了。
代码
形象地看看代码实现吧qwq。。(其实很短)并且因为已经有了顺序,此处可以只加单向边了~
void Build() {
sort(lis + 1, lis + k + 1, Cmp);
for (int i = k; i > 1; -- i) lis[++ k] = Get_Lca(lis[i], lis[i - 1]);
sort(lis + 1, lis + k + 1, Cmp); k = unique(lis + 1, lis + k + 1) - lis - 1;
for (int i = 1; i <= k; ++ i) {
while (top && post[sta[top]] < pre[lis[i]]) -- top;
if (top) add_edge(sta[top], lis[i]); sta[++ top] = lis[i];
}
}应用
对于每次只拿一些特殊点出来,然后对于这些点进行 \(dp\) 或者其他神奇操作的题。
虚树常常是解决这些题的利器。但要注意点数和 \(\sum k\) 不能很大。
它的构建的复杂度是 \(O((\sum k) \times \log n)\) 的,常数也不大。
题目
先咕一会,到时候再填。
咕咕咕