堆与堆排序（一）

上一篇博文浅谈优先队列介绍了什么是优先队列，文末提到了一种数据结构——“堆”，基于“堆”实现的优先队列，出队和入队的时间复杂度都为 O(logN).

这篇博文我们就走进“堆”，看看它到底是什么结构。

此堆非彼堆

值得注意的是，这里的“堆”不是内存管理中提到的“堆栈”的“堆”。前者的“堆”——准确地说是二叉堆，是一种类似于完全二叉树的数据结构；后者的“堆”是一种类似于链表的数据结构。

堆的结构性质

二叉堆在逻辑结构上是一棵完全二叉树。什么是完全二叉树呢？即树的每一层都是满的，除了最后一层最右边的元素有可能缺位。

如下图所示，打错号的两个不是完全二叉树，其他都是。

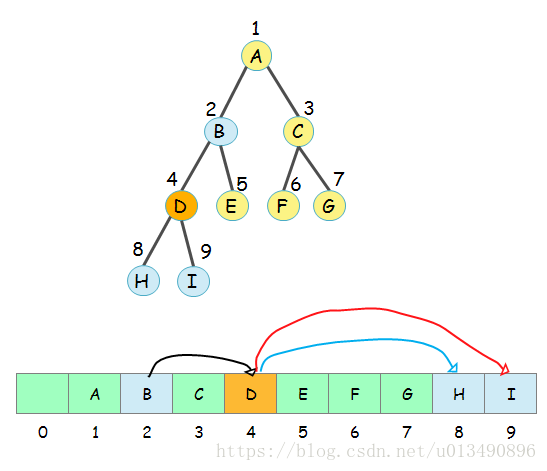
这里写图片描述

对于一个有 N 个节点的完全二叉树，我们可以为它的每个节点指定一个索引，方法是从上至下，从左到右，从1开始连续编号，如下图黑色数字所示。了解二叉树的朋友一定看出来了，这就是二叉树的层序遍历。

可以看出，对于一个有 N 个节点的完全二叉树，索引值和元素是一一对应的。所以完全二叉树可以用一个数组来表示而不需要指针：索引值就是数组的下标，元素的值就是节点的关键字。

如下图，是一个完全二叉树和数组的相互关系。

这里写图片描述

如果你继续观察，就会发现另一个规律：对于数组任一位置 i 上的元素，其左儿子在位置 2i 上，右儿子在2i+1上，它的父亲则在位置 $\lfloor i/2 \rfloor$ 上。

以节点 D 为例，D 的下标是 4.

B是它的父节点，B的下标是2（=4/2），如图中黑色的线；
H是它的左孩子，H的下标是8（=4*2），如图中蓝色的线；
I是它的右孩子，I的下标是9（=4*2+1），如图中红色的线；

堆序性质

二叉堆一般分为两种：最大堆和最小堆。

最大堆：也叫做大根堆。每一个节点的值（或者说关键字）都要大于或等于它孩子的值（对于任何叶子我们认为这个条件都是自动满足的）。下图就是一个最大堆。

这里写图片描述

最小堆：也叫做小根堆。每一个节点的值（或者说关键字）都要小于或等于它孩子的值（对于任何叶子我们认为这个条件都是自动满足的）。下图就是一个最小堆。

这里写图片描述

值得注意的是：以大根堆为例，在任何从根到某个叶子的路径上，键值的序列是递减的（如果允许相等的键存在，则是非递增的）。然而，键值之间并不存在从左到右的次序。也就是说，在树的同一层节点之间，不存在任何关系，更一般地来说，在同一节点的左右子树之间也没有任何关系。

堆的重要特性

以大根堆为例，把堆的重要特性总结如下。

这里写图片描述

只存在一棵 n 个节点的完全二叉树。它的高度等于 $\lfloor \log _2 n \rfloor$
堆的根总是包含了堆的最大元素
堆的一个节点以及该节点的子孙也是一个堆
可以用数组来实现堆，方法是用从上到下、从左到右的方式来记录堆的元素。为了方便起见，可以在这种数组从 1 到 n 的位置上存放堆的元素，留下H[0]，要么让它空着，要么在其中放一个限位器，它的值大于堆中任何一个元素。
在 4 的表示法中：

1) 父母节点的键将会位于数组的前 $\lfloor n/2 \rfloor$ 个位置中，而叶子节点的键将会占据后 $\lceil n/2 \rceil$ 个位置。

2) 在数组中，对于一个位于父母位置 i 的键来说，它的子女将会位于2i和2i+1. 相应地，对于一个位于i的键来说，它的父母将会位于 $\lfloor i/2 \rfloor$

对于上面提到的父母节点的键将会位于数组的前 $\lfloor n/2 \rfloor$ 个位置中，而叶子节点的键将会占据后 $\lceil n/2 \rceil$ 个位置。这一点我觉得很有意思，咱们不严格证明，仅简单分析一下为什么会这样。

设一个堆共有N个元素。判断一个索引为 i 的节点是不是父母节点，可以看它有没有孩子。如果它有孩子，那么2i一定小于等于N，换句话说，如果2i大于N，则可以断定它是叶子节点，在它位置之后的节点（如果有的话）也一定是叶子节点，因为从 2i > N 可以推出 2(i+1) > N，2(i+2) > N，…

所以，只要求解不等式 2i > N，取i的最小值，就得到第一个叶子节点的位置。

经过演算，i 的最小值是 $i=\lfloor N/2 \rfloor +1$ ，所以，最后一个父母节点的位置是 $\lfloor n/2 \rfloor$

如何构造一个堆

针对给定的一列键值，如何构造一个堆呢？

方法一：自底向上堆构造

假设要构造一个大根堆，步骤如下：

在初始化一棵包含 n 个节点的完全二叉树时，按照给定的顺序来放置键；
按照下面的方法，对树进行“堆化”
从最后一个父母节点开始，到根为止，该算法检查这些节点的键是否满足父母优势的要求。如果该节点不满足，就把该节点的键 K 和它子女的最大键进行交换，然后再检查在新的位置上，K 是否满足父母优势要求。这个过程一直继续到对 K 的父母优势要求满足为止（最终它必须满足，因为对每个叶子中的键来说，这条件是自动满足的）。
对于以当前父母节点为根的子树，在完成它的“堆化”以后，对该节点的直接前趋（数组中此节点的前一个节点）进行同样的操作。在对树的根完成这种操作以后，该算法就停止了。

如果该节点不满足父母优势，就把该节点的键 K 和它子女的最大键进行交换，然后再检查在新的位置上，K 是否满足父母优势要求。这个过程一直继续到对 K 的父母优势要求满足为止——这种策略叫做下滤（percolate down）。

假设有一列键（共10个）：4,1,3,2,16,9,10,14,8,7

那么，按照上面给定的键值顺序，对应的完全二叉树如下图。

这里写图片描述

最后一个父母节点是5（=10/2），我们从5号节点开始对这个二叉树进行堆化。

这里写图片描述

看完这些图，相信你已经知道如何构建大根堆了。下面就用C语言来实现。

递归解法

根据上文的算法描述，很容易想到用递归来实现。我们先设计一个函数——下滤函数。

先写几个宏。给定一个位置为 i 的节点，很容易算出它的左右孩子的位置和父母的位置。

#define LEFT(i)    (2*i)   // i 的左孩子
#define RIGHT(i)   (2*i+1) // i 的右孩子
#define PARENT(i)  (i/2)   // i 的父节点

假定以 LEFT(t) 和 RIGHT(t) 为根的子树都已经是大根堆，下面的函数调整以 t 为根的子树，使之成为大根堆。

// 下滤函数（递归解法）
// 假定以 LEFT(t) 和 RIGHT(t) 为根的子树都已经是大根堆
// 调整以 t 为根的子树，使之成为大根堆。
// 节点位置为 1~n，a[0]不使用
void percolate_down_recursive(int a[], int n, int t) 
{
#ifdef PRINT_PROCEDURE
    printf("check %d\n", t);
#endif
    int left = LEFT(t);
    int right = RIGHT(t);   
    int max = t; //假设当前节点的键值最大

    if(left <= n)  // 说明t有左孩子    
    {
        max = a[left] > a[max] ? left : max;
    }

    if(right <= n)  // 说明t有右孩子  
    {
        max = a[right] > a[max] ? right : max;
    }

    if(max != t)
    {   
        swap(a + max, a + t); // 交换t和它的某个孩子，即t下移一层
#ifdef PRINT_PROCEDURE
        printf("%d NOT satisfied, swap it and %d \n",t, max);
#endif
        percolate_down_recursive(a, n, max); // 递归，继续考察t
    }
}


//交换*a和*b, 内部函数
static void swap(int* a, int* b) 
{
    int temp = *a;
    *a = *b;
    *b = temp;
}

有了上面的函数，我们就可以从最后一个父母节点开始，到根为止，逐个进行“下滤”。

非递归解法

以上代码是用“交换法”（第26行）对节点进行下滤。一次交换需要3条赋值语句，有没有更好的写法呢？有，就是“空穴法”（我自己起的名字）。我们先说明空穴法的原理，然后附上代码。

以上图中“检查1号节点，不满足”这个地方开始，对1号节点进行下滤。

这里写图片描述

// 非递归且不用交换
void percolate_down_no_swap(int a[], int n, int t) 
{
    int key = a[t];  // 用key记录键值
    int max_idx;
    int heap_ok = 0;  // 初始条件是父母优势不满足
#ifdef PRINT_PROCEDURE      
    printf("check %d\n", t);
#endif  
    // LEFT(t) <= n 成立则说明 t 有孩子
    while(!heap_ok && (LEFT(t) <= n))
    {           
        max_idx = LEFT(t); // 假设左右孩子中，左孩子键值较大
        if(LEFT(t) < n)    // 条件成立则说明有2个孩子
        {
            if(a[LEFT(t)] < a[RIGHT(t)])
                max_idx = RIGHT(t); //说明右孩子的键值比左孩子大

        }//此时max_idx指向键值较大的孩子

        if(key >= a[max_idx])
        {
            heap_ok = 1; //为 key 找到了合适的位置，跳出循环
        }
        else
        {   
            a[t] =  a[max_idx]; //孩子上移一层，max_idx 被空出来，成为空穴  

#ifdef PRINT_PROCEDURE                  
            printf("use %d fill %d \n", max_idx, t);
            printf("%d is empty\n", max_idx);
#endif              
            t = max_idx; //令 t 指向空穴     
        }               
    }

    a[t] = key; // 把 key 填入空穴
#ifdef PRINT_PROCEDURE                  
    printf("use value %d fill %d \n", key, t);

#endif      

    return;
}