堆、堆排序、优先队列

1. 堆

严格来说，堆也有不同的种类。本文所说的堆指的是二叉堆。

二叉堆本质上是完全二叉树，可以分为两种类型：

最大堆（大顶堆）
最小堆（小顶堆）

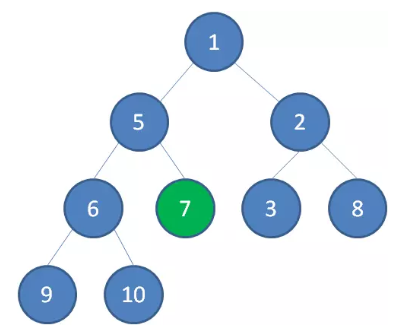
二叉堆的根节点叫做堆顶。最大堆和最小堆的特点，决定了在最大堆的堆顶是整个堆中的最大元素；最小堆的堆顶是整个堆中的最小元素。

1.1 最大堆

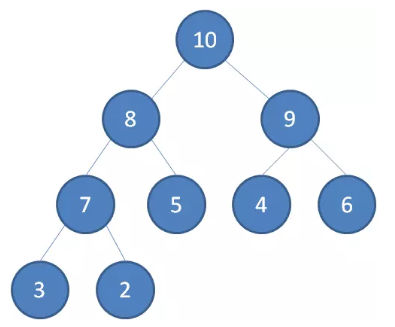
最大堆任何一个父节点的值，都大于等于它左右孩子节点的值。

在这里插入图片描述

1.2 最小堆

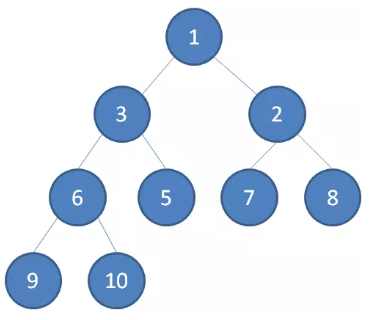
最小堆任何一个父节点的值，都小于等于它左右孩子节点的值。

在这里插入图片描述

2. 堆的逻辑结构与物理存储

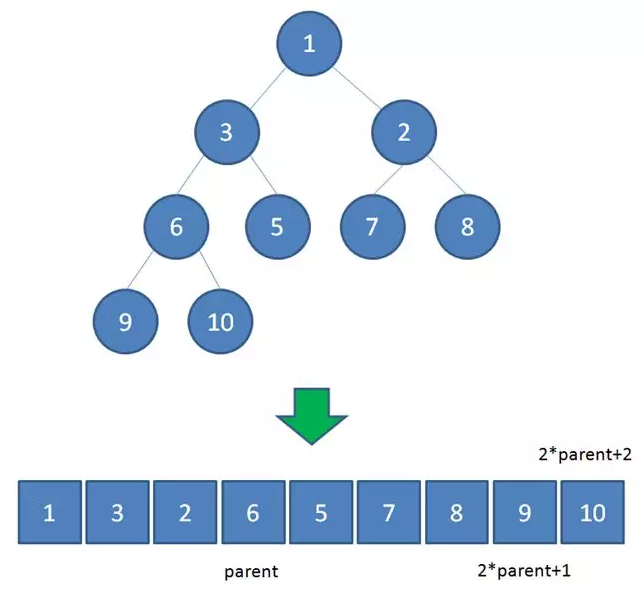
二叉堆在逻辑上虽然是一颗完全二叉树，但它的存储方式并不是链式存储，而是顺序存储。换句话说，二叉堆的所有节点都存储在数组当中。

树的节点是按从上到下、从左到右的顺序紧凑排列的。

在这里插入图片描述

利用数组下标作为节点编号，假设父节点的下标是parent，则有

左儿子的下标 = 2 * parent + 1
右儿子的下标 = 2 * parent + 2

3. 堆的操作

对于堆，有两种主要操作：

插入节点 push
删除节点 pop

这两种操作都是基于堆的自我调整完成的。

4. 堆的操作的复杂度

堆的插入和删除两种操作所花的时间和树的深度正比。

因此，如果一共有 $n$ 个元素，那么堆的深度为 $logn$ ，则每个操作可以在 $O(logn)$ 的时间完成。

5. 堆的自我调整

以最小堆为例，看看堆是如何进行自我调整的：

5.1 插入节点

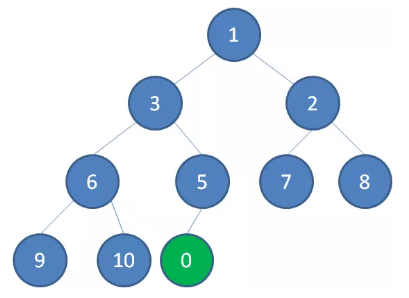
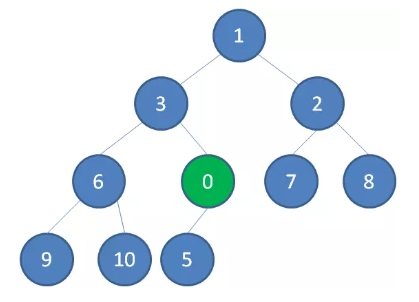
二叉堆的节点插入，插入位置是完全二叉树的最后一个位置。比如我们插入一个新节点，值是 0。

在这里插入图片描述

这时候，我们让节点0的它的父节点5做比较，如果0小于5，则让新节点“上浮”，和父节点交换位置。

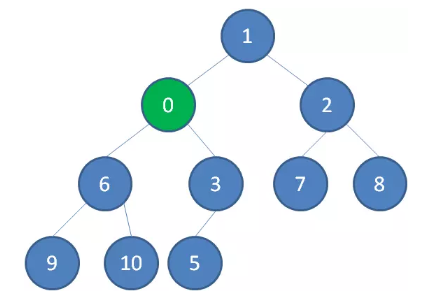
在这里插入图片描述

继续用节点0和父节点3做比较，如果0小于3，则让新节点继续“上浮”。

在这里插入图片描述

继续比较，最终让新节点0上浮到了堆顶位置。

在这里插入图片描述

5.2 删除节点

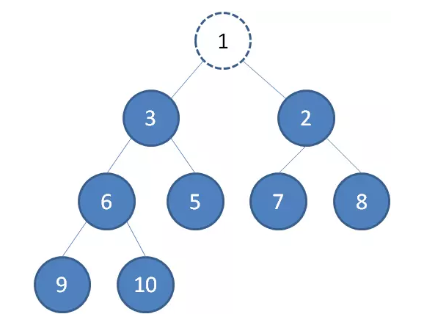
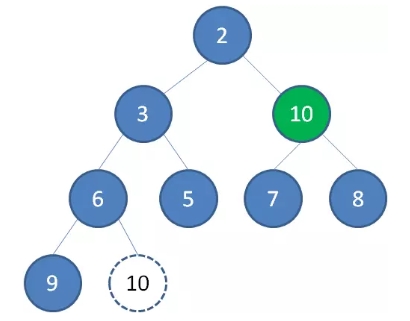
二叉堆的节点删除过程和插入过程相反，所删除的是处于堆顶的节点。比如我们删除最小堆的堆顶节点1。

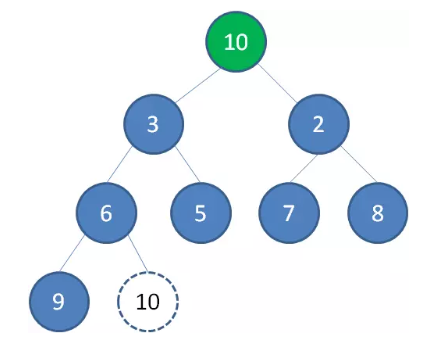
在这里插入图片描述

这时候，为了维持完全二叉树的结构，我们把堆的最后一个节点10补到原本堆顶的位置。

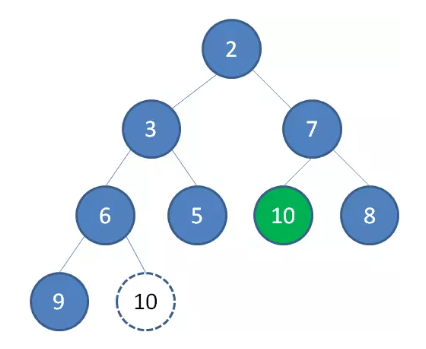
在这里插入图片描述

接下来我们让移动到堆顶的节点10和它的左右孩子进行比较，如果左右孩子中最小的一个（显然是节点2）比节点10小，那么让节点10“下沉”。

在这里插入图片描述

继续让节点10和它的左右孩子做比较，左右孩子中最小的是节点7，由于10大于7，让节点10继续“下沉”。

在这里插入图片描述

这样一来，堆重新得到了调整。

从上面的分析可知，显然不管是插入还是删除操作，堆的自我调整都与深度成正比，故时间复杂度为 $O(logn)$ 。

5.3 参考实现

最小堆参考实现，最大堆类似

public class MinimumHeap {

    private int[] heap;
    private int size = 0;

    /**
     * Creates a heap of specified capacity
     * @param heapMaxSize The maximum capacity of the initialization heap
     */
    public MinimumHeap(int heapMaxSize){
        heap = new int[heapMaxSize];
    }

    /**
     * floating
     * @param i Index of its own node
     * @param x The value to insert
     */
    private void floating(int i, int x){
        while (i > 0){
            //父节点的索引下标
            int p = (i - 1) / 2;
            //如果已经没有大小颠倒则退出
            if(heap[p] <= x) break;
            //把父亲节点的数值放下来，而把自己提上去
            heap[i] = heap[p];
            i = p;
        }
        heap[i] = x;
    }

    /**
     * sinking
     * @param x The value to move to the root
     */
    private void sinking(int x){
        int i = 0;
        while (i * 2 + 1 < size){
            //比较子节点的值
            int a = i * 2 + 1, b = i * 2 + 2;
            if(b < size && heap[b] < heap[a]) a = b;
            //如果已经没有大小颠倒则退出
            if(heap[a] >= x) break;
            //把子节点的数值提上来
            heap[i] = heap[a];
            i = a;
        }
        heap[i] = x;
    }

    public void push(int x){
        floating(size++, x);
    }

    public int pop(){
        int res = heap[0];
        sinking(heap[--size]);
        return res;
    }

    public int top(){
        return heap[0];
    }

    public boolean isEmpty(){
        return size == 0;
    }

    public static void main(String[] args){
        int[] arr = new int[]{1, -2, 3, 10, -4, 7, 2, -5};
        MinimumHeap heap = new MinimumHeap(arr.length + 1);
        for (int e: arr) heap.push(e);
        while (!heap.isEmpty()){
            System.out.print(heap.pop() + " ");
        }
        //Output: -5 -4 -2 1 2 3 7 10 
    }
    
}

6. 堆排序

6.1 构建二叉堆

构建二叉堆，也就是把一个无序的完全二叉树调整为二叉堆，本质上就是让所有非叶子节点依次下沉。

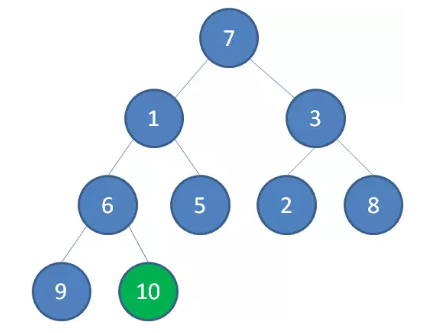
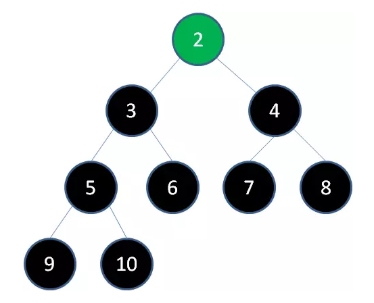
我们举一个无序完全二叉树的例子：

在这里插入图片描述

首先，我们从最后一个非叶子节点开始，也就是从节点10开始。如果节点10大于它左右孩子中最小的一个，则节点10下沉。

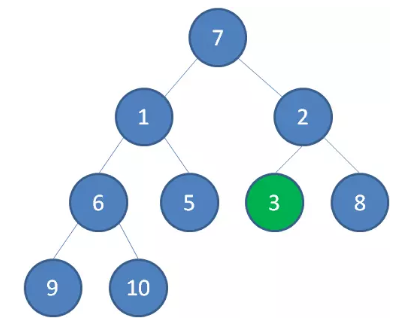
在这里插入图片描述

接下来轮到节点3，如果节点3大于它左右孩子中最小的一个，则节点3下沉。

在这里插入图片描述

接下来轮到节点1，如果节点1大于它左右孩子中最小的一个，则节点1下沉。事实上节点1小于它的左右孩子，所以不用改变。

接下来轮到节点7，如果节点7大于它左右孩子中最小的一个，则节点7下沉。

在这里插入图片描述

节点7继续比较，继续下沉。

在这里插入图片描述

至此，一颗无序的完全二叉树就构建成了一个最小堆。

6.2 堆排序过程

堆排序是利用堆的自我调整实现的。

例如给定一个数组，对数组进行排序，使数组元素从小到大排列。

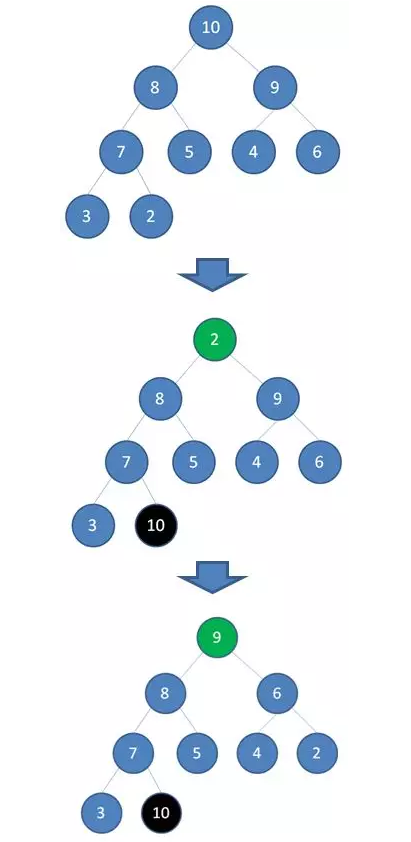
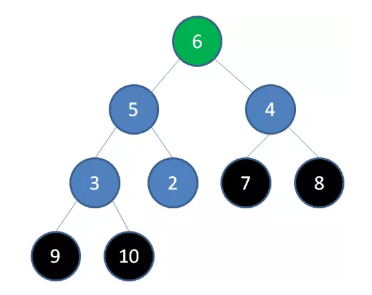
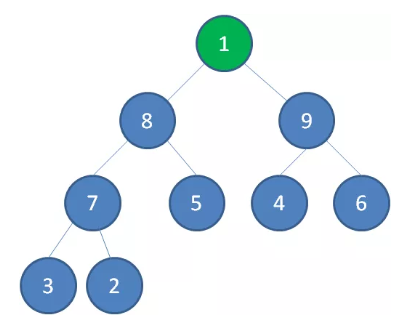
首先，我们要根据给定的数组构建一个最大堆。当我们删除一个最大堆的堆顶（并不是完全删除，而是替换到最后面），经过自我调节，第二大的元素就会被交换上来，成为最大堆的新堆顶。

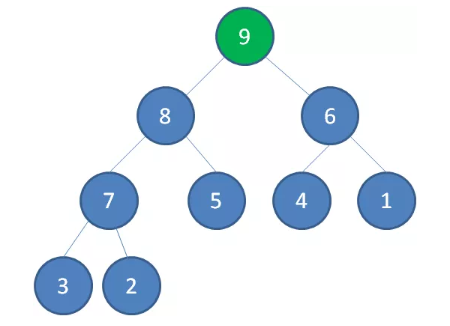
在这里插入图片描述

如上图所示，当删除值为10的堆顶节点，经过调节，值为9的新节点就会顶替上来；当删除值为9的堆顶节点，经过调节，值为8的新节点就会顶替上来…

由于二叉堆的这个特性，我们每一次删除旧堆顶，调整后的新堆顶都是大小仅次于旧堆顶的节点。那么我们只要反复删除堆顶，反复调节二叉堆，所得到的集合就成为了一个有序集合，过程如下：

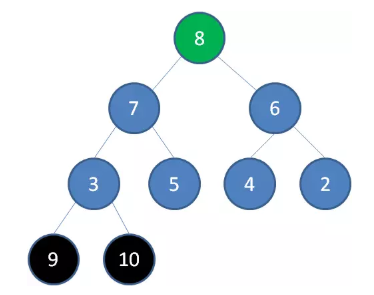
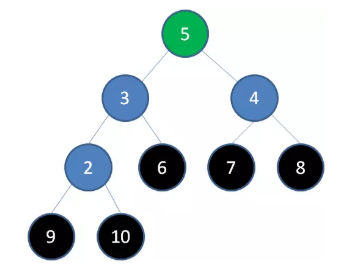
删除节点9，节点8成为新堆顶：

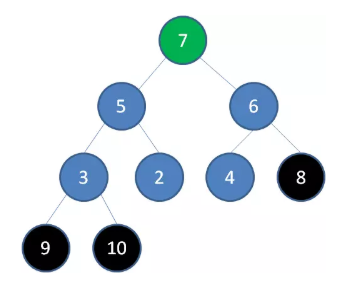
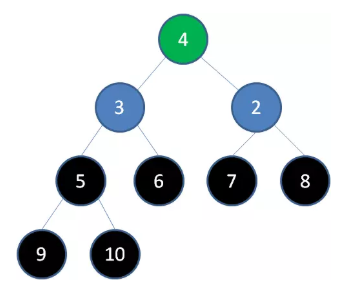
在这里插入图片描述

删除节点8，节点7成为新堆顶：

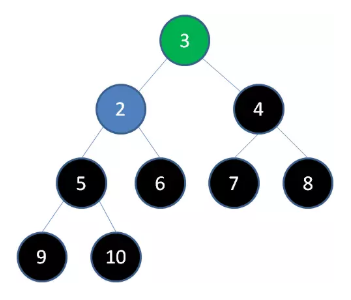
在这里插入图片描述

删除节点7，节点6成为新堆顶：

在这里插入图片描述

删除节点6，节点5成为新堆顶：

在这里插入图片描述

删除节点5，节点4成为新堆顶：

在这里插入图片描述

删除节点4，节点3成为新堆顶：

在这里插入图片描述

删除节点3，节点2成为新堆顶：

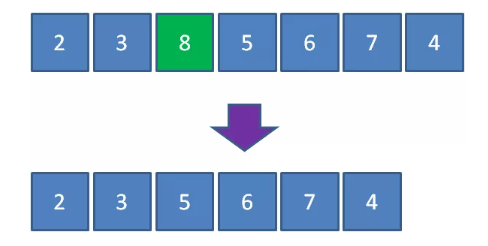
在这里插入图片描述

至此，原本的最大堆已经变成了一个从小到大的有序集合。之前说过二叉堆实际存储在数组当中，数组中的元素排列如下：

在这里插入图片描述

6.3 算法步骤

根据无序数组构建二叉堆
循环删除堆顶元素，移到数组尾部，调节堆产生新的堆顶

6.4 参考实现

import java.util.Arrays;

public class MaximumHeapSort {

    public static void swap(int[] arr, int i, int j){
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

    /**
     * sinking
     * @param heap The Heap to be adjusted
     * @param i The index of value which need to be sunk
     * @param x The value to be sunk
     * @param size The current valid size of heap
     */
    private static void sinking(int[] heap, int i, int x, int size){
        while (i * 2 + 1 < size){
            int a = i * 2 + 1, b = i * 2 + 2;
            //定位到最大的孩子节点
            if(b < size && heap[b] > heap[a]) a = b;
            //如果当前节点大于等于最大孩子节点，说明调整完毕
            if(heap[a] <= x) break;
            heap[i] = heap[a];
            i = a;
        }
        heap[i] = x;
    }

    /**
     * Build a heap according to an array
     * @param arr An array to form a heap
     */
    private static void buildHeap(int[] arr){
        for (int i = arr.length / 2 - 1; i >= 0; i--){
            sinking(arr, i, arr[i], arr.length);
        }
    }

    /**
     * Heap sort
     * @param arr Unsorted array
     */
    public static void sort(int[] arr){
        //根据无序数组构建二叉堆
        buildHeap(arr);
        //循环删除堆顶元素，移到数组尾部，调节堆产生新的堆顶
        for (int i = arr.length - 1; i > 0; i--){
            //最后一个元素和堆顶元素交换
            swap(arr, i, 0);
            //下沉调整最大堆
            sinking(arr, 0, arr[0], i);
        }
    }

    public static void main(String[] args){
        int[] arr = new int[]{10, 8, 9, 7, 5, 4, 6, 3, 2};
        MaximumHeapSort.sort(arr);
        System.out.println(Arrays.toString(arr));
    }

}

6.5 堆排序的复杂度

空间复杂度

因为没有开辟额外的集合空间，所以空间复杂度为 $O(1)$
时间复杂度

堆排序所需要的时间主要有两部分组成，一是构建二叉堆的时间，二是循环删除并进行堆维护的时间。
- 第一步，把无序数组构建成二叉堆，需要进行 $n/2$ 次循环。每次循环调用一次 sinking 方法，所以第一步的计算规模是 $(n/2) * logn$ ，时间复杂度 $O(nlogn)$ 。
  
  这里只是初略地把每个非叶子节点下沉的时间复杂度都当成 $O(logn)$ ，事实上经过严格的证明构建堆的时间复杂是 $O(n)$ ，但这里我们初略算出的复杂度为 $O(nlogn)$ ，当然我们算出的复杂度也是正确的，只不过是不够精确而已。
  
  $O(n)$ 的证明也比较简单，可以参考：
  
  https://blog.csdn.net/LinuxTiger/article/details/7172258
- 第二步，需要进行 $n-1$ 次循环。每次循环调用一次 sinking 方法，所以第二步的计算规模是 $(n-1)*logn$ ，时间复杂度 $O(nlogn)$ 。
总的时间复杂度为：
$O(n) + O(nlogn) = O(nlogn)$

6.6 堆排序和快排对比

排序方法	平均情况	最好情况	最坏情况	辅助空间	稳定性
堆排序	$O(nlogn)$	$O(nlogn)$	$O(nlogn)$	$O(1)$	不稳定
快速排序	$O(nlogn)$	$O(nlogn)$	$O(n^2)$	$O(logn) \sim O(n)$	不稳定

相同点
- 堆排序和快速排序的平均时间复杂度都是 $O(nlogn)$
- 两者都是不稳定的排序
- 快速排序因为递归所以需要额外的空间开销 $O(logn) \sim O(n)$ ；堆排序是就地排序，空间复杂度 $O(1)$
不同点
- 堆排序在最好、最坏、平均情况下时间复杂度都是 $O(nlogn)$ ；快排在最坏情况下是 $O(n^2)$ ，最好情况下是 $O(nlogn)$

7. 优先队列

7.1 优先队列种类

优先队列不再遵循队列先入先出(FIFO)的原则，而是分为两种情况：

最大优先队列，无论入队顺序，当前最大的元素优先出队。
最小优先队列，无论入队顺序，当前最小的元素优先出队。

比如有一个最大优先队列，它的最大元素是8，那么虽然元素8并不是队首元素，但出队的时候仍然让元素8首先出队：

在这里插入图片描述

要满足以上需求，利用线性数据结构并非不能实现，但是时间复杂度较高，最坏时间复杂度O（n），并不是最理想的方式。

7.2 利用堆的特性实现优先队列

堆的特性：

最大堆的堆顶是整个堆中的最大元素
最小堆的堆顶是整个堆中的最小元素

因此，可以用最大堆来实现最大优先队列，最小堆实现最小优先队列。

例如，利用最大堆实现优先队列，每一次入队操作就是堆的插入操作，每一次出队操作就是删除堆顶节点。

7.2.1 入队操作

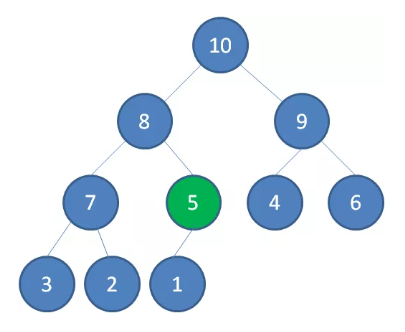
插入新节点5

在这里插入图片描述

新节点5上浮到合适位置

在这里插入图片描述

7.2.2 出队操作

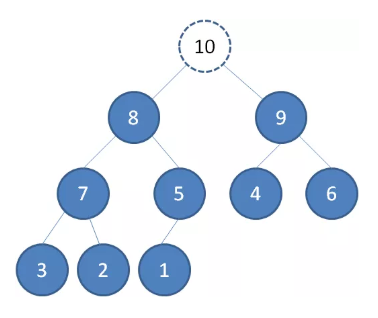
把原堆顶节点10“出队”

在这里插入图片描述

最后一个节点1替换到堆顶位置

在这里插入图片描述

节点1下沉，节点9成为新堆顶

在这里插入图片描述

7.3 优先队列的时间复杂度

因为二叉堆节点上浮和下沉的时间复杂度都是 $O(logn)$ ，所以优先队列入队和出队的时间复杂度也是 $O(logn)$

7.4 参考实现

import java.util.Arrays;

public class PriorityQueue {

    private static final int DEFAULT_CAPACITY = 16;

    private int[] queue;
    private int size;

    /**
     * Constructs an empty queue with the default capacity.
     */
    public PriorityQueue(){
        this.size = 0;
        this.queue = new int[DEFAULT_CAPACITY];
    }

    /**
     * Constructs an empty queue with the specified initial capacity.
     * @param capacity the initial capacity of the queue
     */
    public PriorityQueue(int capacity){
        this.size = 0;
        this.queue = (capacity > 0) ? new int[capacity] : new int[DEFAULT_CAPACITY];
    }

    /**
     * floating
     * @param i Index of its own node
     * @param x The value to insert
     */
    private void floating(int i, int x){
        while (i > 0){
            int p = (i - 1) / 2;
            if(queue[p] >= x) break;
            queue[i] = queue[p];
            i = p;
        }
        queue[i] =  x;
    }

    /**
     * sinking
     * @param x The value to move to the root
     */
    private void sinking(int x){
        int i = 0;
        while (2 * i + 1 < size){
            int a = 2 * i + 1, b = 2 * i + 2;
            if(b < size && queue[b] > queue[a]) a = b;
            if(queue[a] <= x) break;
            queue[i] = queue[a];
            i = a;
        }
        queue[i] = x;
    }

    /**
     * Increases the capacity of the queue
     */
    private void resize(){
        this.queue = Arrays.copyOf(this.queue, this.size * 2);
    }

    public void push(int x){
        if(size == queue.length) resize();
        floating(size++, x);
    }

    public int pop(){
        int res = queue[0];
        sinking(queue[--size]);
        return res;
    }

    public int front(){
        return queue[0];
    }

    public boolean isEmpty(){
        return size == 0;
    }

    public static void main(String[] args){
        int[] arr = new int[]{1, -2, 3, 10, -4, 7, 2, -5};
        PriorityQueue queue = new PriorityQueue();
        for (int e: arr) queue.push(e);
        while (!queue.isEmpty()){
            System.out.print(queue.pop() + " ");
        }
    }

}

8. References

https://mp.weixin.qq.com/s/23CwW5eSv-lI6vaZHzSwhQ

https://mp.weixin.qq.com/s/PWuuChodYGMr8iJzW2VW9Q

https://mp.weixin.qq.com/s/CdK1l2kB3aCUtBORjS4DVQ