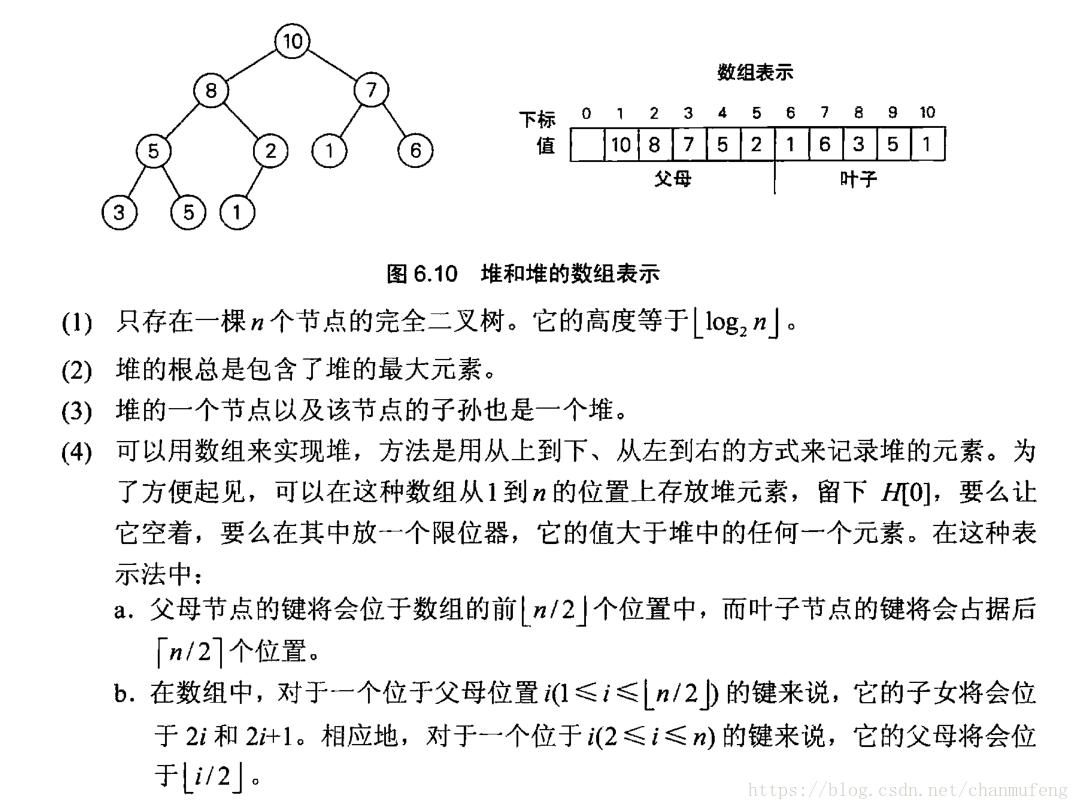
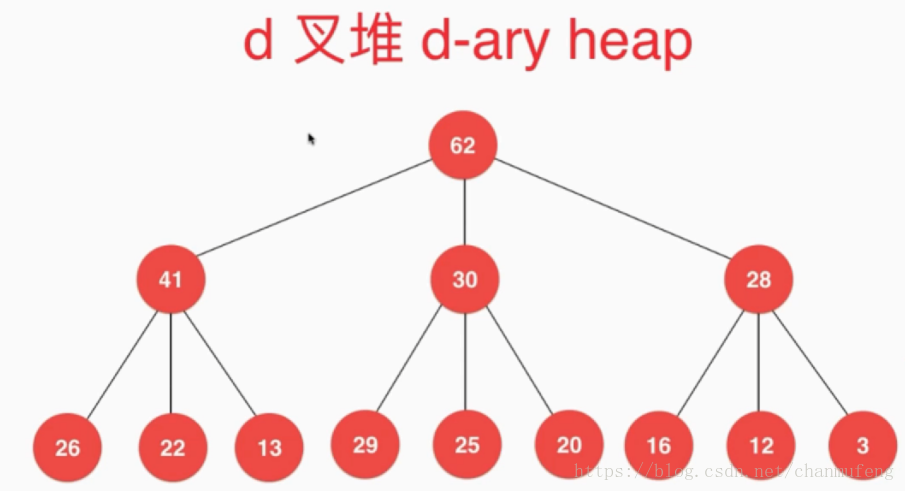
完整代码参见github
堆的概念
定义
堆就是一棵二叉树,每个节点包含一个键,不过还需要满足以下两个条件:
(1)必须是完全二叉树,也就是说,树的每一层都必须是满的,除了最后一层最右边的元素可能有所缺失
(2)堆特性(又称为父母优势,这里我们以最大堆为例),每一个节点都要大于或等于它的子节点(对于叶子节点我们认为是满足这个条件的)
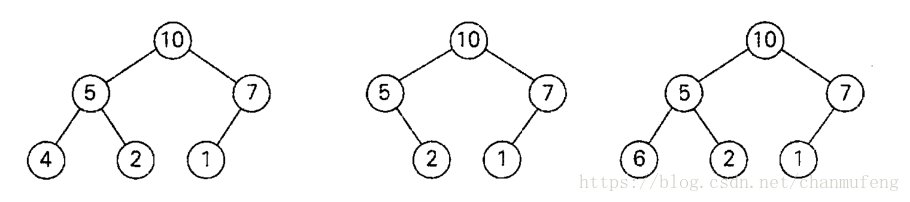
举例说明,上图中只有第一棵树是堆,第二棵树违背了完全二叉树条件,第三棵树也不是堆,因为节点5小于它的子节点6,堆特性条件不满足。
需要注意的是,从根到某叶子节点的路径上,键值的序列是递减的(非递增)的,但是同一层的节点之间或者不同层之间无父子(或祖先后代)关系的节点之间美哦与任何顺序联系!
堆的特征
堆的构造
经典的堆构造往往采用数组的实现方式,并且下标从1开始(数组第一个元素闲置)
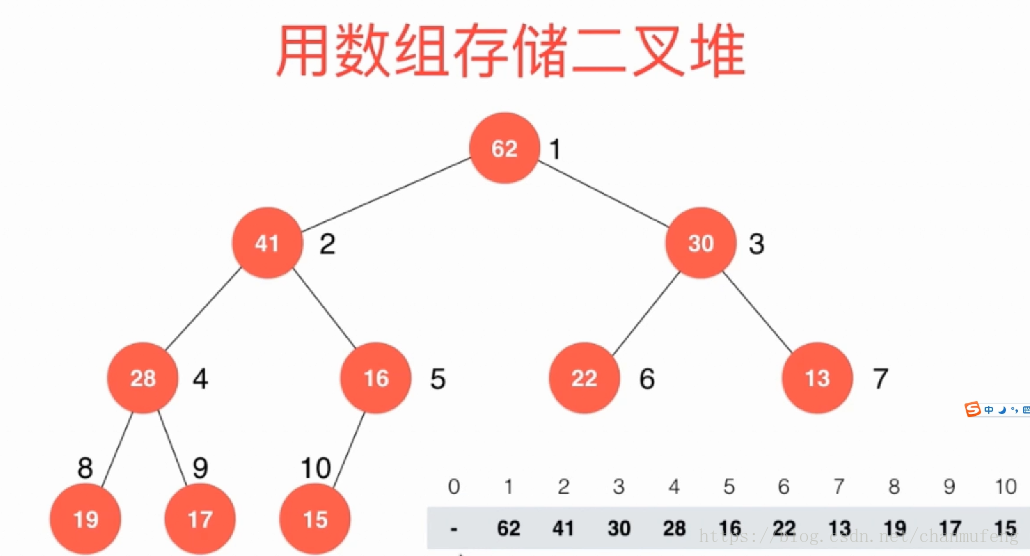
堆的构造方法通常有两种,一种是元素逐个进行插入,另一个是用heapify对整个数组进行初始化。
1 插入构造法
代码如下:
#include <iostream>
#include <algorithm>
#include <cassert>
template <typename Item>
class MaxHeap {
private:
Item* data;
//堆的实际容量(不包括data[0])
int capacity;
//堆目前的元素数量
int count;
void shiftUp(int index) {
while (index > 1) {
if (data[index] > data[index / 2])
std::swap(data[index],data[index / 2]);
index /= 2;
}
}
void shiftDown(int index) {
while (index * 2 <= count) {
int j =2 * index;
if (j + 1 <= count && data[j] < data[j + 1]) {
j++;
}
if (data[j] <= data[index]) {
break;
}
std::swap(data[j],data[index]);
index = j;
}
}
public:
MaxHeap(int capacity) {
this -> capacity = capacity;
data = new Item[capacity + 1];
count = 0;
}
~MaxHeap() {
delete [] data;
}
//插入元素
void insert(Item item) {
assert(count < capacity);
data[++count] = item;
//将item浮动到合适的位置
shiftUp(count);
}
//弹出根元素
Item pop() {
assert(count > 0);
Item root = data[1];
data[1] = data[count];
count--;
shiftDown(1);
return root;
}
void print() {
for (int i = 1; i <= count; i++) {
std::cout << data[i] << " ";
}
}
//获取堆的当前大小
int size() {
return count;
}
//判断堆是否为空
bool isEmpty() {
return count == 0;
}
};将 个元素逐个插入到堆中,时间复杂度为
接下来我们就可以直接利用最大堆的根节点最大的特点编写堆排序
堆排序-版本一
template <typename T>
template heapSort1(T arr[],int n){
MaxHeap<T> maxHeap = MaxHeap<T>(n);
for (int i = 0;i < n;i++){
maxHeap.insert(arr[i]);
}
for (int i = n - 1;i >= 0;i--){
arr[i] = maxHeap.pop();
}
}Heapify将数组转换为堆结构
之前我们都是将元素逐个加入到数组中,然后利用shiftUp进行堆结构的整理,但更好的做法是直接在原数组中将数组整理为堆结构,这个过程叫做Heapify
我们将原来不满足堆结构的数组以完全二叉树的结构进行表示,如下图所示:
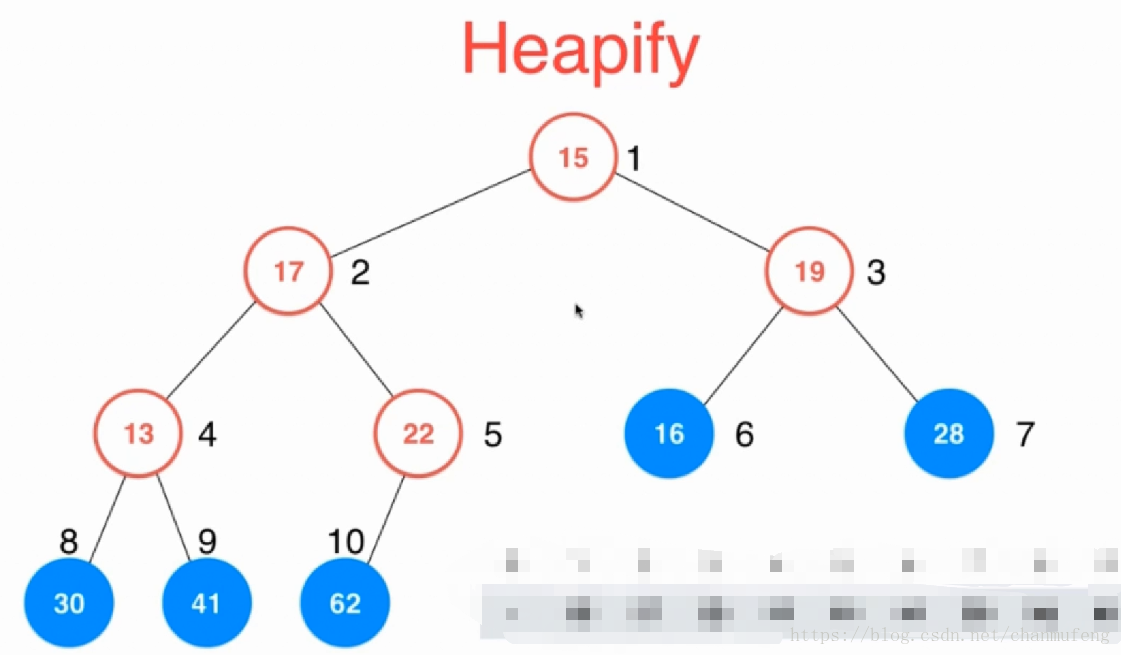
通过观察,可以发现,所有的叶子节点都满足堆结构,从第一个不是叶子节点的节点(索引为5的节点22)开始不满足堆结构,因此,从该节点开始我们不断进行shiftDown操作,直到根节点,这样我们就完成了对数组进行堆结构整理的操作。
我们将该过程整理成MaxHeap类的另一个构造方法,代码如下:
//利用数组进行堆的初始化
MaxHeap(Item arr[],int n) {
data = new Item[n + 1];
this -> capacity = n;
this -> count = n;
for (int i = 0; i < n; i ++) {
data[i + 1] = arr[i];
}
//从第一个不是叶子节点的节点开始向上,逐次使用shiftDown方法
for (int i = count / 2; i > 0 ; i --) {
shiftDown(i);
}
}用heapipy方法,时间复杂度为
堆排序-版本二
template <typename T>
template heapSort2(T arr[],int n){
MaxHeap<T> maxHeap = MaxHeap<T>(arr,n);
for (int i = n - 1;i >= 0;i--){
arr[i] = maxHeap.pop();
}
}堆排序-最终版
//堆排序算法--最终版
//在原数组中进行堆排序,不占用额外空间
//首先对原数组进行heapify
//然后将arr[0]和最后一个元素进行交换,重新对第一个元素进行heapify,以此类推
//注意:索引从0开始
//左子树:2 * i + 1
//右子树:2 * i + 2
//父节点:(i - 1) / 2
#include <iostream>
#include <cassert>
template <typename T>
void __shiftDown(T arr[],int n,int index) {
while (2 * index + 1 < n) {
int j = 2 * index + 1;
if (j + 1 < n && arr[j] < arr[j + 1])
j++;
if (arr[index] > arr[j]) {
break;
}
std::swap(arr[index],arr[j]);
index = j;
}
}
template <typename T>
void heapSort(T arr[] ,int n) {
//从第一个不是叶子节点的元素开始向上,对每个节点进行shiftDown
for (int i = (n - 1) / 2; i >= 0; i--) {
__shiftDown(arr, n, i);
}
for (int i = n - 1; i > 0 ; i --) {
std::swap(arr[i], arr[0]);
__shiftDown(arr, i, 0);
}
}
索引堆
什么是索引堆?
与普通堆只存储元素不同,索引堆是将元素和其索引同时存储的数据结构(多用一个数组来保存元素的索引)。
为什么需要索引堆?
我们以普通堆为例进行说明,普通堆构造之前的数据存储如下图所示
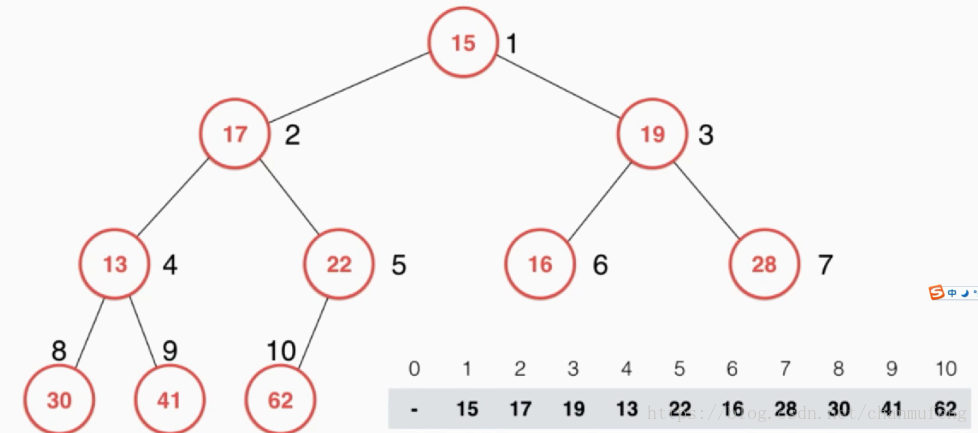
我们用数组存储堆的元素,随后我们将数组进行堆构造
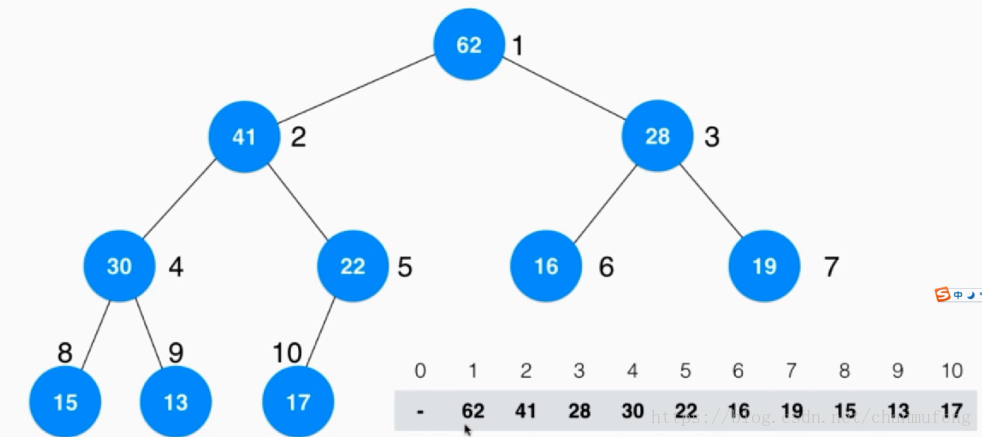
我们看到,数组以堆的形式进行了重构,但这在某些特殊情形下可能会带来一些麻烦。
比如,我们存储的元素是一篇上万字的文章,那么对文章进行交换位置的开销是相当大的;再比如,原始数组的元素表示的是计算机的进程,其数组索引表示的该进程的id号,当我们按照堆对其进行重构之后,我们无法确定排列之后的元素(进程)的id号是多少,因此诸如改变某个id为3的进程的优先级的这种操作便不太灵活(除非我们对存储的元素进行数据结构封装,使其同时存储id号,但同样还是带来了元素交换的效率问题),这时候我们的索引堆就派上了用场。
索引堆的构造
这里我们仍然以最大堆为例。
索引堆底层用两个数组进行表示,一个用来存储元素的索引(数组从索引1开始存储),另一个(数组从索引1开始存储)用来存储元素,我们对存储索引的数组进行堆的构造(对int类型的数据进行交换是很高效的),存储元素的数组我们不改变其存储的顺序,图示如下:
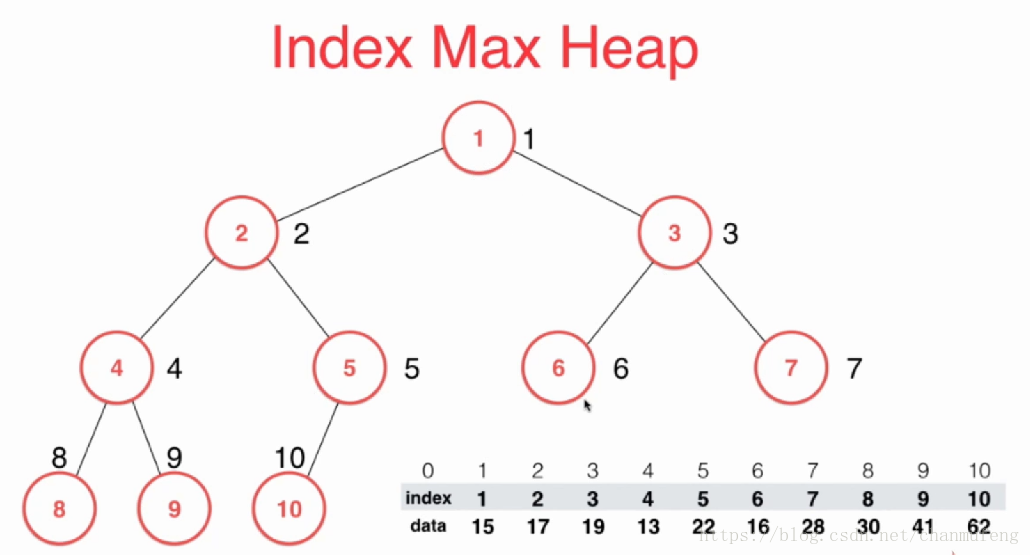
我们用heapify对索引数组进行堆构造,完成之后的图示如下:
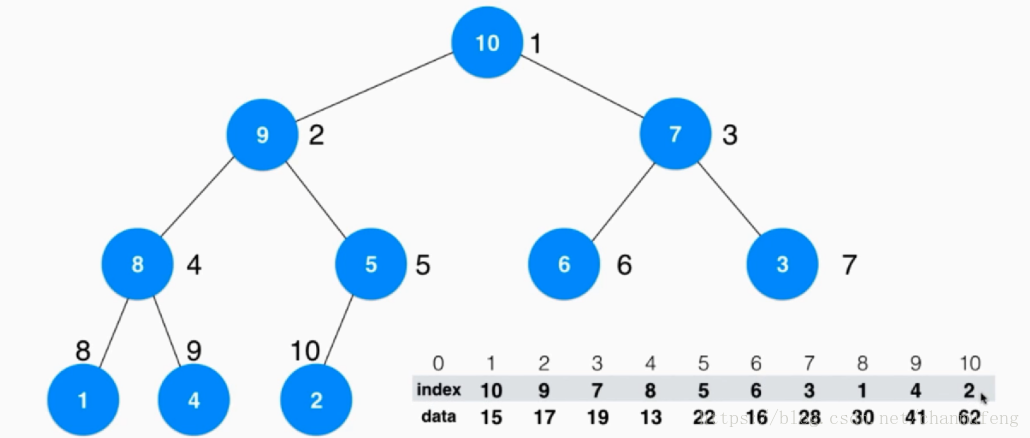
代码如下:
#include <iostream>
#include <algorithm>
#include <cassert>
template <typename Item>
class IndexMaxHeap{
private:
//存储元素的数组
Item* data;
//存储元素索引的数组
int* indexes;
//当前堆中元素个数
int count;
//堆容量
int capacity;
void shiftUp(int i){
while(i > 1){
if (data[indexes[i]] > data[indexes[i / 2]]){
std::swap(indexes[i],indexes[i / 2]);
}
i /= 2;
}
}
void shiftDown(int i){
int j = 0;
while (2 * i <= count){
j = 2 * i;
if (j + 1 <= count && data[indexes[j]] < data[indexes[j + 1]])
j += 1;
if (data[indexes[i]] >= data[indexes[j]])
break;
std::swap(indexes[i],indexes[j]);
i = j;
}
}
public:
IndexMaxHeap(int capacity){
data = new Item[capacity + 1];
indexes = new int[capacity + 1];
this -> capacity = capacity;
this -> count = 0;
}
~IndexMaxHeap(){
delete [] data;
delete [] indexes;
}
int size(){
return count;
}
//注意,对用户而言,i是从0开始的,但我们存储是从1开始,编程实需要注意
void insert(int i,Item item){
assert(count < capcacity);
assert(i > 0 && i + 1 < capcacity);
data[++i] = item;
indexes[++count] = i;
shiftUp(count);
}
Item pop(){
assert(count > 0);
Item root = data[indexes[1]];
indexes[1]=indexes[count];
count--;
shiftDown(1);
return root;
}
//返回最大元素的索引
int popMaxIndex(){
assert(count > 0);
//注意,对用户来说从0开始
int root = indexes[1] - 1;
indexes[1] = indexes[count];
std::swap(indexes[1],indexes[count]);
count--;
shiftDown(1);
return root;
}
Item getItem(int i){
return data[i + 1];
}
//修改索引为i的item
//O(n)
void change(int i,Item newItem){
data[++i] = newItem;
//接下来我们需要找到newItem(即data[i]在indexes中的位置)
//indexes[j] = i,j表示的就是data[i]在堆中的位置
//将i尝试shiftUp操作或者shiftDown
for (int j = 1;j < count; j++){
if (indexes[j] == i ){
shiftUp(j);
shiftDown(j);
}
}
}
}这里我们在class中加入了一个比较常用的操作change,将data中索引为i的元素改为newItem,我们采用遍历indexes的做法来找到indexes的下标j,这个j表示的是我们更改的newItem的索引在indexes中的存储位置,即
data[index[j]] = newIndex
这样一来change操作的时间复杂度就是
能不能有更快的操作方法呢?
reverse表

如上图,rev数组就是index(就是indexes)数组的一个reverse表(当然反过来说也是正确的),其实就是索引和元素值的调换而已,
index[i] = j;
reverse[j] = i;但经过这样存储,我们可以通过 的时间复杂度找到index中的索引。
举个例子:
假如我更改了data数组中下标为4的元素13的值为100,那么为了维持堆的性质,data数组可以不变,我们必须对index数组进行重构,那我们就需要知道100的下标(4)在index中的存储位置j,然后对j进行shiftUp或shiftDown试探(总有一个会有效)。
如果我们不用reverse表的方法,我们需要从头遍历index数组,直到我们遇到index[j] == 4,此时我们得到 j=9。
如果我们采用reverse表的方式,我们要找4在index中的存储位置,直接利用reverse[4]就可以得到,时间复杂度为
最后一点优化
我们上面写的代码中,getItem(int i)和change(int i,Item newItem)函数其实有一点小瑕疵,如果我们输入的参数i并没有存储在indexes数组中,那么我们的程序就会出错
因此我们需要编写一个函数来检验i是否在堆(indexes)中,这里我们用到了reverse数组
详细代码见ReverseIndexMaxHeap.h
bool isContains(int i){
assert(i + 1 >=1 && i + 1 <=capacity);
return reverse[i + 1] != 0;
}和堆相关的其他问题
1 优先队列
2 在N个元素当中选出前M个元素
构造一个仅含有M个元素最小堆,不断将N个元素进行insert,插入完成之后在堆中的即为前M个元素,算法时间复杂度为
3 多路归并
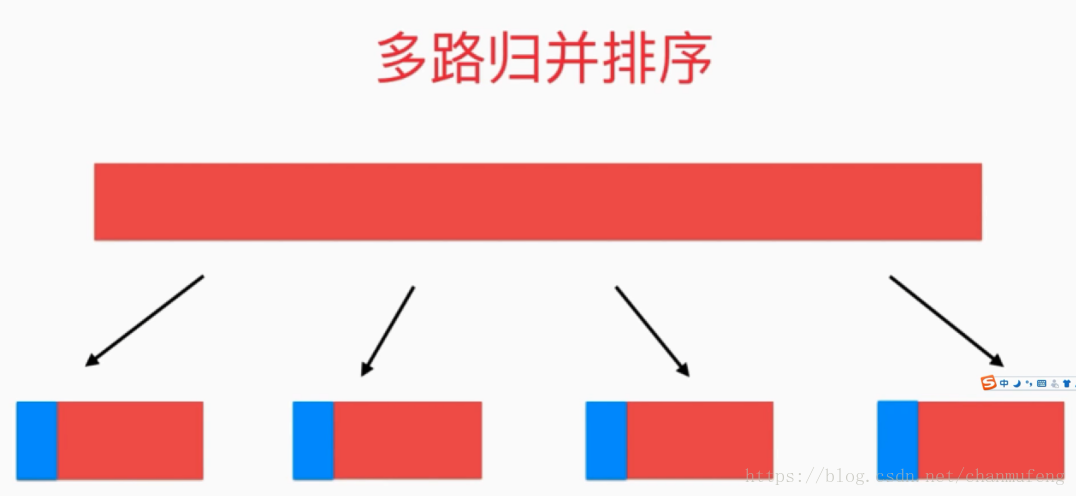
之前我们都是使用二路归并,比较两个子数组中的最小值(非减排序),然后将最小值添加到原数组中的对应位置。
如果我们在这里使用4路归并,一个更好的方法是将子数组的第一个元素放入一个最小堆中,每次从堆中取出一个最小的元素,判断该元素属于哪个子数组,然后取出该数组中的另一个元素放入最小堆中,然后逐步完成归并。
更极端一点,对于N个元素的数组,如果我们使用N路归并,也就是说每个子数组只有一个元素,我们将N个元素植入堆中进行排序,此时归并排序也就退化成为堆排序。