一、斐波那契数列
由于斐波纳挈数列是以兔子的繁殖引入的,因此也叫“兔子数列”。它指的是这样一个数列:0,1,1,2,3,5,8,13……从这组数可以很明显看出这样一个规律:从第三个数开始,后边一个数一定是在其之前两个数的和。在数学上,斐波纳挈数列可以以这样的公式表示:F(0) = 0
F(1) = 1 F(n) = F(n-1) + F(n-2),(n>=2)
二、斐波纳挈数列的实现
既然该数列已经有这样一个规律:F(n) = F(n-1) + F(n-2);那么我们很容易就能想到用递归的方法,这样写出来的代码比较简洁
long long Fib1(long long num)
{
assert(num >= 0); //断言
//递归
if ((num == 1) || (num == 0))
{
return num;
}
return Fib1(num-1)+Fib1(num-2);
} 当然,我们也可以这样写:
long long Fib1(long long num)
{
assert(num >= 0);
//递归
return num<2 ? num:(Fib1(num-1)+Fib1(num-2)); //三目运算符
} 这样的递归算法虽然只有简单的几行,但是效率却很低。为什么呢?我们可以分析其递归调用的时间复杂度: O(2^N)
由于使用递归时,其执行步骤是:要得到后一个数之前必须先计算出之前的两个数,即在每个递归调用时都会触发另外两个递归调用,例如:要得到F(10)之前得先得到F(9)、F(8),那么得到F(9)之前得先得到F(8)、F(7)……如此递归下去
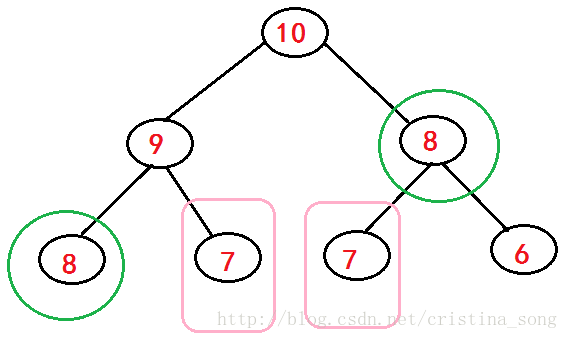
从上图我们可以看出,这样的计算是以 2 的次方在增长的。除此之外,我们也可以看到,F(8)和F(7)的值都被多次计算,如果递归的深度越深,那么F(8)和F(7)的值会被计算更多次,但是这样计算的结果都是一样的,除了其中之一外,其余的都是浪费,可想而知,这样的开销是非常恐怖的!
所以,如果在时间复杂度和空间复杂度都有要求的话,我们可以用以下两种非递归算法来实现:
时间复杂度为O(N),空间复杂度为O(N)
创建一个数组,每次将前两个数相加后直接赋给后一个数。这样的话,有N个数就创建一个包含N个数的一维数组,所以空间复杂度为O(N);由于只需从头向尾遍历一边,时间复杂度为O(N)
long long* Fib2(long long num)
{
assert(num >= 0);
//非递归
long long* array = new long long[num+1];
array[0] = 0;
array[1] = 1;
for (int i=2; i<=num; i++)
{
array[i] = array[i-1] + array[i-2];
}
return array;
} 时间复杂度为O(N),空间复杂度为O(1)
借助两个变量 first 和 second ,每次将 first 和 second 相加后赋给 third ,再将 second 赋给 first ,third 赋给 second,如此循环。
long long Fib3(long long num)
{
assert(num >= 0);
long long first = 0;
long long second = 1;
long long third = 0;
for(int i=2; i<=num; i++)
{
third = first + second;
first = second;
second = third;
}
return third;
}