小凯的疑惑
同余:设m是给定的一个正整数,a、b是整数,若满足m|(a-b),则称a与b对模m同余,记为a≡b(mod m),或记为a≡b(m)。这个式子称为模m的同余式,若m∤ (a-b),则称a、b对模m不同余,同余概念又常表达为:
1.a=b+km(k∈Z);<=>a=b(mod m);
2.a和b被m除时有相同的余数。<=>a%m=b%m;
—百度百科。
题目简述:
求最大的n不能用ax+by表示,a,b互质
解:n!=ax+by =>n-ax!=by => (n-ax)%b!=0
令 m=n-ax;
m%b!=0,求max m
miller–robin算法
费马小定理
费马小定理:对于质数p和任意整数a,有a^p ≡ a(mod p)(同余)。反之,若满足a^p ≡ a(mod p),p也有很大概率为质数。
将两边同时约去一个a,则有a^(p-1) ≡ 1(mod p)
也即是说:假设我们要测试n是否为质数。我们可以随机选取一个数a,然后计算a^(n-1) mod n,如果结果不为1,我们可以100%断定n不是质数。
二次探测定理:
如果p是奇素数,则 x^2 ≡ 1(mod p)的解为 x ≡ 1 或 x ≡ p - 1(mod p)
如果a^(n-1) ≡ 1 (mod n)成立,Miller-Rabin算法不是立即找另一个a进行测试,而是看n-1是不是偶数。如果n-1是偶数,令u=(n-1)/2,并检查是否满足二次探测定理即a^u ≡ 1 或 a^u ≡ n - 1(mod n)。
栗子:
假设n=341,我们选取的a=2。则第一次测试时,2^340 mod 341=1。由于340是偶数,因此我们检查2^170,得到2^170 mod 341=1,满足二次探测定理。同时由于170还是偶数,因此我们进一步检查2^85 mod 341=32。此时不满足二次探测定理,因此可以判定341不为质数。
将这两条定理合起来,也就是最常见的Miller-Rabin测试。

实现:
例题:
解:
解:
欧几里得算法
扩展欧几里得
- 求逆元:
传送门:逆元
2.模意义上的行列式 ,模为合数。
3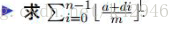
狄利克雷卷积
积性函数:对于函数f(n),若满足对任意互质的数字a,b,n=a*b且f(n)=f(a)*f(b),那么称函数f为积性函数。显然f(1)=1。
定义f,g两个函数的狄利克雷卷积(∗)(∗)运算为:
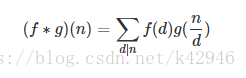
狄利克雷卷积的性质:
交换律:f∗g=g∗f
结合律:(f∗g)∗h=f∗(g∗h)
分配率:f∗(g+h)=f∗g+f∗h
单位元:f∗e=e∗f
若f,g均为积性函数,则f∗g也为积性函数。 常见的狄利克雷卷积:
基本计数原理
博客借鉴: 传送门

