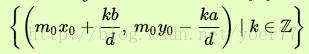【数论初步】

一、欧几里得 (链接)

1.欧几里得算法

int gcd(int a,int b)
{
    return b?gcd(b,a%b):a; 
}

2.扩展欧几里得算法

    //先得到更底层的x2,y2,再根据计算好的x2,y2计算x1，y1。
    //推理2，递推关系
LL exgcd(LL a,LL b,LL &x,LL &y)
{
    if(!b)
    {
        x=1;y=0;
        return a;
    }
    LL ret=exgcd(b,a%b,y,x);
    y-=a/b*x;
    return ret;
}

3.贝祖等式

d0 是 a 和 b 的最大公约数。
在方程ax+by=m中，如果 m=m0d0，那么方程显然有无穷多个解：

这里写图片描述

(X0和Y0为扩展欧几里得求出来的特解)

4.扩欧的乘法逆元

【逆元】设我们要求a/b%p的值，我们可以转化为a*x%p。显然，(1/b)%p=x%p,x*b%p=1。

前提：gcd(x,b)=1.这样的话，x就存在。

如何求解a*x%n=1的方程呢？我们可以化成ax+ny=1，然后在上述gcd中带出。（逆元：x=(x%p+p)%p;）

二、素数（链接）

1.欧拉函数

对正整数n，欧拉函数是小于或者等于n的数中与n互质的数的个数.

$\small \varphi \left ( n \right )=n\left ( 1-\frac{1}{p1} \right )\left ( 1-\frac{1}{p2} \right )\cdot \cdot \cdot \left ( 1-\frac{1}{pk} \right )$

2.埃氏筛选（O(n*logn*logn))

const int N = 1e+6 + 7;
int pri[N],cnt;
bool isp[N];
void init_pri()
{
    for(int i=2; i<N; i++)
        if(!isp[i])
        {
            pri[++cnt]=i;
            for(int j=i+i;j<N;j+=i)isp[j]=true;
        }
}

3.欧拉筛选（O(n)）

void init_pri(int n)
{
    cnt=0;
    for(int i=2; i<=n; i++)
    {
        if(!isp[i])
            pri[++cnt]=i;
        for(int j=1; j<cnt; j++)
        {
            long long k=1LL*i*pri[j];
            if(k>n)break;
            isp[k]=true;
            if(i%pri[j]==0)break;
        }
    }
}

4.Miller Rabbin(判断大素数)

# define ll long long
ll mypow(ll a,ll b,ll m)
{
    if(b==0)
        return 1;
    if(b==1)
        return a%m;
    ll temp=mypow(a,b/2,m);
    temp*=temp;
    temp%=m;
    if(b&1)
        temp*=a;
    temp%=m;
    return temp;
}
bool Miller_Rabbin(ll x)
{
    if(x==2)
        return true;        ///2要直接判断
    for(int i=1;i<=50;++i){
        ll a=rand()%(x-2)+2;
        if(mypow(a,x-1,x)!=1)
            return false;
    }
    return true;
}
int main()
{
    ll n;
    while(scanf("%lld",&n)!=EOF)
    {
        if(Miller_Rabbin(n))
            cout<<"Yes"<<endl;
        else
            cout<<"No"<<endl;
    }
    return 0;
}

三、逆元 ( 链接)

1.费马小定理：假如p是质数，且gcd(a,p)=1，那么 a(p-1)≡1（mod p）。即：假如a是整数，p是质数，且a,p互质(即两数只有一个公约数1)，那么a的(p-1)次方除以p的余数恒等于1。当膜P为素数时有a^(p-1)=1（mod p）那么a^(p-2)=a^-1(mod p)

也就是说a的逆元为a^(p-2)。一般P较大时用快速幂求逆元。

typedef  long long ll;
ll pow_mod(ll x, ll n, ll MOD)
{
    ll ret=1;
    while(n>0)
    {
        if(n&1)ret=ret*x%MOD;
        x=x*x%MOD;
        n>>=1;
    }
    return ret;
}

2.逆元打表

typedef  long long ll;  
const int N = 1e5 + 5;  
int inv[N];  
   
void inverse(int n, int p) {  
    inv[1] = 1;  
    for (int i=2; i<=n; ++i) {  
        inv[i] = (ll) (p - p / i) * inv[p%i] % p;  
    }  
}

四、中国剩余定理（链接）

1.当m1,m2,m3互质时

typedef long long LL;
LL exgcd(LL a,LL b,LL &x,LL &y)
{
    if(!b)
    {
        x=1;y=0;
        return a;
    }
    LL ret=exgcd(b,a%b,y,x);
    y-=a/b*x;
    return ret;
}
LL CRT(LL a[],LL m[],int n)   /*模数为m，余数为a x%m=a */
{
    LL M=1,ans=0;
    for(int i=1;i<=n;i++)M*=m[i];
    for(int i=1;i<=n;i++)
    {
        LL x,y;
        LL Mi=M/m[i];
        exgcd(Mi,m[i],x,y);
        ans=(ans+Mi*x*a[i])%M;
    }
    if(ans<0)ans+=M;
    return ans;
}

2.线性同余方程

typedef long long LL;
LL a[N],m[N]; /*模数为m，余数为a x%m=a */
LL exgcd(LL a,LL b,LL &x,LL &y)
{
    if(!b)
    {
        x=1,y=0;
        return a;
    }
    LL ret=exgcd(b,a%b,y,x);
    y-=a/b*x;
    return ret;
}
bool solve(LL &m0,LL &a0,LL m,LL a)
{
    LL x,y;
    LL gcd=exgcd(m0,m,x,y);
    if((a-a0)%gcd)return false;
    x*=(a-a0)/gcd;
    x%=m/gcd;
    a0=a0+x*m0;
    m0*=m/gcd;
    a0=(a0%m0+m0)%m0;
    return true;
}
bool MLES(LL &m0,LL &a0,int n)  /* 有解返回true，并且x=a0+k*m*/
{
    bool flag=true;
    m0=1;a0=0;
    for(int i=1;i<=n;i++)
    if(!solve(m0,a0,m[i],a[i]))
    {
        return false;
    }
    return true;
}

猜你喜欢