平衡树介绍
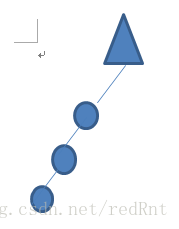
前几篇的文章我们介绍了一下二叉树和二叉搜索树。现在假设我们要建立一棵BST,依次插入下列数据:
20, 33, 50, 61, 87, 99
那么按照BST的规则我们可以得到下列的BST:
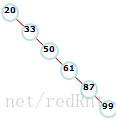
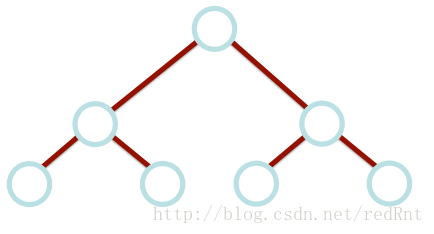
如果你问我,这是一棵二叉搜索树吗?这肯定的。但是它更像什么?链表!有什么区别呢?数据结构不同,链表只包含一个指向下一个节点的指针,而这个包含的还有指向左节点的指针。这个时候我们看看,我们之前定义的方法效率有没有变化?当然有,而且效率会被大大降低。因为我们之前执行的方法都是要遍历左右子树的,而这种树压根就没有左子树,遍历左子树显得太多此一举。举个例子,我们之前写过一个函数 isContains(),它的作用是遍历二叉搜索树,然后找到对应的节点。如果它是正常的二叉搜索树的结构,那么执行该方法的算法复杂度就是O(logN),但是如果是上图所示的结构那么就是链表的遍历为O(N)。
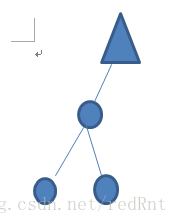
只有在树的每一层左右子树高度相同的情况下,用于实现BST查找算法才能达到理想的性能.因此我们应该想办法避免上述情况的发生,尝试将上面的类型转换成我们常见的二叉树。但是有时候这样的结构同样会带来一系列的问题,如下图:
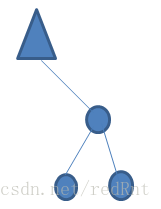
这棵树的要求满足上面的左右子树高度相同,但是仅限于在树根上的满足。对比上图并没有改变什么。所以们还要满足这样的一个条件:保证每个节点必须有相同高度的左右子树(因此只有具有2k-1节点的完美平衡的树才能满足条件),如下图所示
所以我们给平衡二叉树下个定义:
它类似二叉搜索树,唯一不同的就是,对于每一个节点,它的左右子树的高度差不超过1.(那么如果树空呢?左右子树为0,当然也是平衡二叉树,而且高度定义为1)
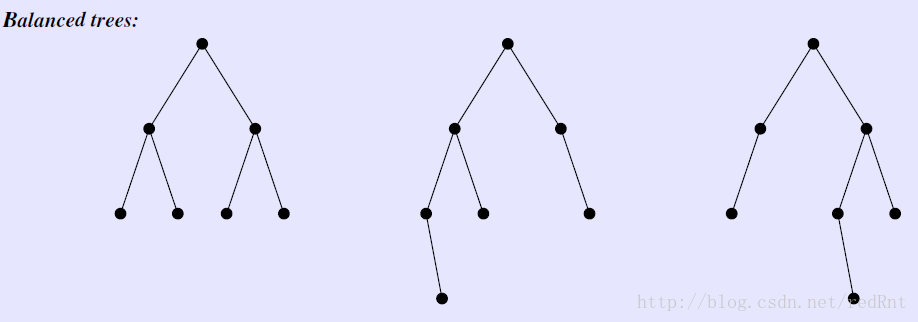
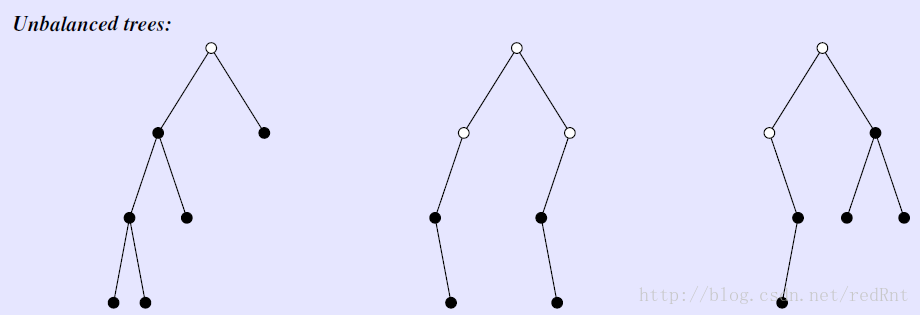
下图列举了一些平衡和非平衡二叉树的图例:
如果忘记了什么叫树的高度可以回头看看数据结构——树(4)——什么是树?
先来分析一下为什么这三棵不是平衡树。最左边的那棵树,左子树的高度为3,后面两棵树不平衡在于,对于根节点他们的高度差符合,但是它的子节点不平衡(例如图二中,树根下面的空心的节点,它左子树高度为2,右子树高度为0)
平衡二叉树和AVL算法
刚刚提到,如果我们应用BST,在最坏的情况下,我们插入和查找的算法复杂度都是O(N),因为那时候变成了线性查找。树状结构也就没什么意义了。要完全发挥BST的性能优点,最好的办法就是避免最坏情况的发生。换句话说我们只要时刻保持树的高度平衡,那么就永远不会出现最坏的情况。
第一个树平衡算法是由俄罗斯数学家Georgii Adelson-Velskii和Evgenii Landis于1962年发表的。算法的名称就用两位科学家的名字首字母命名为AVL算法。因此AVL是一个平衡树算法,AVL树又称为高度平衡树。
下面我们就来看看在一棵平衡二叉树中插入一个新节点会发生什么。
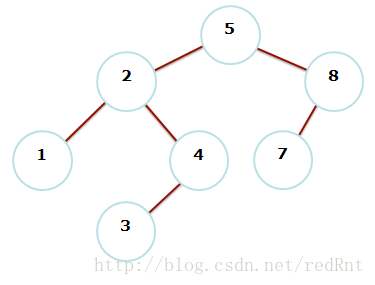
- 当我们插入一个节点到AVL树中时,我们必须更新平衡树的信息,比如节点树啊,深度等等
- 我们也必须适当的维护AVL树的平衡结构! (这是很棘手的一个问题),假设我们考虑在上面的树中插入数字6,显然这会扰乱节点8处的平衡。
- 事实证明,树的简单修改(称为旋转)可以恢复AVL的平衡属性
- 插入之后,只有插入路径上的节点可能会改变它们的平衡,因为只有那些节点改变了它们的子树。我们可以根据平衡条件重新平衡。(比如插入6,只会对8路径之后的平衡造成破坏,而左子树跟根节点那边的平衡却完全不受影响)
AVL旋转过程
假设现在存在一棵非平衡的二叉树α,我们要调用某个节点使其达到平衡状态。因为任何节点至多有两个孩子,二叉树不平衡要求α的两个子树的高度相差两以上,所以可能有四个违规情况:
- 插入到α的左侧子的左侧子树中。
- 插入α的左侧子元素的右侧子树中。
- 插入到右侧子树的左侧子树中。
- 插入右侧子树的右侧子树
看下图,假设三角形代表二叉搜索树中已经平衡的部分,那么上面出现不平衡的部分情况1 跟4对应下面的两幅图,这类问题称为外部问题(“outside” cases ),即L-L,R-R(Left-left,right-right).
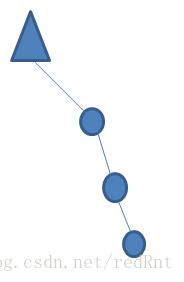
情况2跟3对应的分别是这样的情况,即内部问题(“inside” cases ),L-R,L,R
针对外部问题,我们采用单旋转的方法(single rotation)
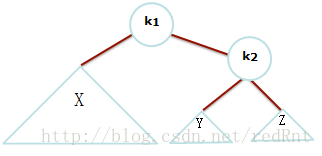
我们先看这样一幅图:
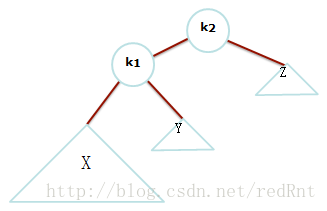
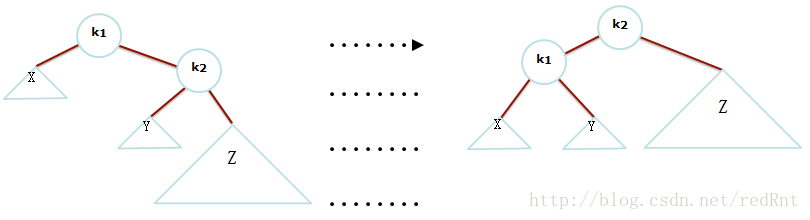
图中X三角形比其他的三角形比较大,意思是X部分代表更大的子树,你可以把X,Y想象成两个节点,Z为两个串起来的节点。显然k2违反了AVL属性,因为高度X已经变得比Z更深了2层.所以我们我们想把X上升一个水平,Z下降一个水平,这样这棵树就平衡了。具体的做法是:
- 我们这样想象:抓住k1摇晃,想象这是一个天平,存在重力。好,那么k1现在是新的根。 在图中,k2> k1(因为k1在k2的左子树中),所以k2成为k1的右边孩子。 X和Z分别保持为k1和k2的左边和右边的孩子。 Y可以放置为K2的左边的孩子,这样的话BST的顺序要求得以满足。如下图:
下面用实际例子来说明一下这个过程,看下图:
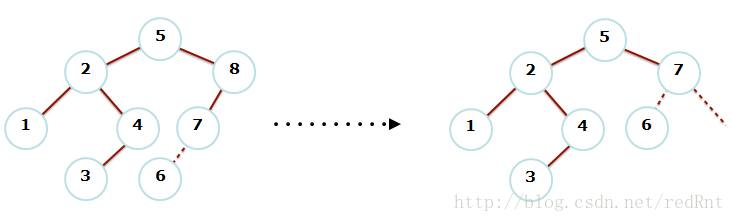
解释:我们尝试在一棵平衡的BST中插入一个新的节点6,按照BST的规则,应该在7的左侧插入(如左边的图)。那么这样就造成了树的不平衡,因为8 7 6出现了LL结构,但是其他的地方的平衡却不受影响,因此我们可以将其他的地方想象成一个大三角形,我们只需要处理8 7 6这三个地方的不平衡问题(因为影响的是8以后的平衡)。按照刚刚提到的做法,我们把7这个节点提起来,向8的右侧旋转,作为这棵子树的树根,所以6在7的左侧,8在右侧,变成右边的额图,这样二叉树就平衡了。
同样的,RR问题的解决方式是一样的,就不再多提了(拿着k2向k1的左侧旋转):
针对内部问题我们采用双旋转法(Double Rotation)
现在假设我们遇到下面左图这样的情况:
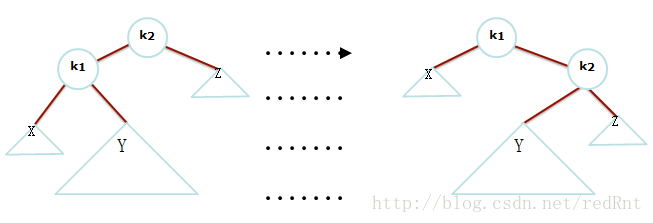
这个时候,不平衡点出现在k2,如果我们按照上面的步骤,进行单旋,那么会造成右图的问题。原因就是Y的深度太大,直接进行单侧旋转会使得深度加深适得其反。这个时候我们采用双旋转法解决这个问题。
双旋转法可以从两个视角去看待:
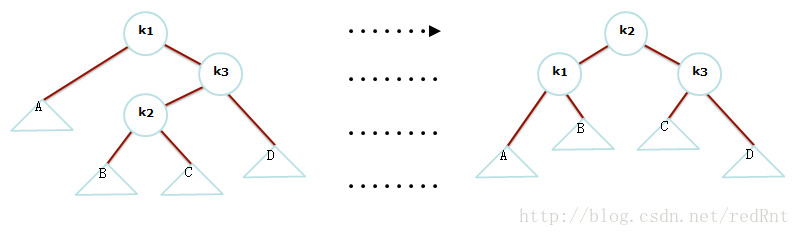
1. 看成是一次复杂的旋转,同样是上图,与其我们看成三棵树(xzy),还不如把这里看成4棵树,即将y分开,以k3作为节点连上。我们既不能让k1称为树根,也不能让k2称为树根,那么我们就让k3称为新的树根:
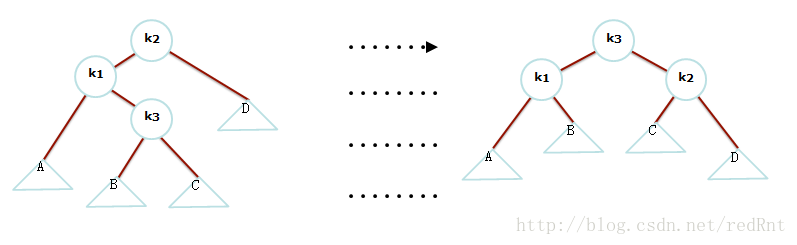
2. 看成是两次简单的单旋转法,我们同样的可以两次旋转,这里我们看到,k1是不平衡的,所以我们先将k3向右旋转,再将k1向左旋转。
下一篇,我将尝试用C++把这部分的代码写写,并且试着看看有没有更好的解释AVL的方法