2.5 图
2.5.1 图的一些概念
经过图中各边一次且恰好一次的环路称为欧拉环路。
经过图中各顶点一次且恰好一次的环路称为哈密尔顿环路。
对于无向图,每一对顶点至少贡献一条边,故总共不超过n(n-1)/2条边,这个上界由完全图达到。对于有向图,至多可能有n(n-1)条边。
2.5.2 图的ADT接口
图支持的操作接口分为边和顶点2类,常见的总结如下:
图ADT支持的边操作接口 |
图ADT支持的顶点操作接口 |
e()//边总数 exist(v,u)//判断联边(v,u)是否存在 insert(v,u)//引入从定点v到u的联边 remove(v,u)//删除从定点v到u的联边 status(v,u)//边(v,u)的状态 weight(v,u)//边(v,u)的权重 |
n()//顶点总数 insert(v)//在顶点集V中插入新顶点v indegree(v)//顶点v的入度 outdegree(v)//顶点v的出度 firstNbr(v)//顶点v的首个邻接顶点 nextNbr(v,u)//在v的邻接顶点中,u的后继 parent(v)//顶点v在遍历树中的父节点 |
typedef enum {UDDISCOVERED,DISCOVERED,VISITED} VStatus;//顶点状态VStatus;枚举类型
typedef enum {UNDETERMINED,TREE,CROSS,FORWARD,BACKWARD} EStatus;//边状态
template <typename Tv,typename Te>//顶点类型、边类型
class Graph
{
private:
void reset()//所有顶点和边的复位
{
for(int i=0;i<n;i++)//对于所有顶点
{status(i)=UNDISCOVERED;dTime(i)=fTime(i)=-1;//状态、时间标签
parent(i)=-1;priority(i)=INT_MAX;//在遍历树中的父节点和优先级数
for (int j=0;j<n;j++)//对于所有边
if(exist(i,j)) statue(i,j)=UNDETERMINED;
}
……
};2.5.3 图的邻接矩阵
图的邻接矩阵利用的是封装好的Vector结构,在内部将所有顶点组织为一个向量V[],同时通过嵌套定义,将所有的边组织为一个二维向量E[][],即邻接矩阵。基于邻接矩阵实现的图结构请参考《数据结构C++语言版》。
2.5.4 广度优先搜索(BFS)
越早被访问到的顶点,其邻居越优先被选用。
从图中顶点S的BFS搜索过程如下:首先访问顶点s,再依次访问s所有的尚未访问到的邻居,再按后者被访问的先后次序,逐个访问它们的邻居。仍未被访问的邻居构成的集合称为波峰集(frontier)。BFS搜索过程可以等效地理解为:反复从波峰集中找到最早被访问到的顶点v,若其邻居已被访问,则将其逐出波峰集;否则任意选择一个尚未被访问到的邻居,并将其加入到波峰集。BFS相当于数结构的层次遍历。
BFS是一种分层查找的过程,每向前走一步可能会访问到一批顶点,不像深度优先搜索DFS那样有回退的情况,因此它不是一个递归的算法,为了实现逐层的访问,算法必须借助一个辅助队列并且以非递归的方式来实现。
例 2.5.1分析下图使用BFS搜索后的遍历结果
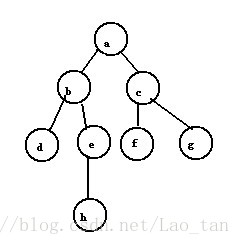
假设从顶点a开始访问,a先入队列。此时队列非空,取队头元素a,由于b,c和a直接相邻且未被访问,因此b,c依次入队。队列非空,取出队头元素b,依次访问与b相邻且未被访问的顶点d,e,并将d,e入队。此时队列非空,取出队头元素c,访问与c相邻且未被访问的顶点f,g,并将f,g入队。此时取队头元素d,但是与d相邻且未被访问的顶点为空,,故不在进行任何操作。继续取出队头元素e,将h入队。最后的便利结果为:abcdefgh。
BFS的空间复杂度为O(n),采用邻接表时时间复杂度为O(n+e)。
2.5.5 深度优先搜索(DFS)
以顶点s为基点的DFS搜索,首先将访问顶点s,再从s所有未被访问到的邻居中任取一个点,并以之为基点,递归地执行DFS算法。故各点被访问到的次序类似于树的先序遍历。每次深度优先搜索的结果必然是图的一个连通分量。其基本思路如下:
首先访问图中某一个起始顶点v,然后从v出发,访问与v相邻的且未被访问的任一项顶点w1,再访问w1邻接且未被访问的任一顶点w2,重复该过程。当不能再继续向下访问时,依次退回到最近被访问的顶点,若它还有邻接顶点未被访问过,则从该点开始继续上述搜索过程,直到图中所有顶点都被访问过。
例 2.5.2分析下图使用DFS搜索后的遍历结果

首先访问a,并设置a为已访问。然后访问与a相邻且未被访问的顶点b,设置b为已访问,然后再访问与b邻接且未被访问的顶点d,置d为已访问。此时d已经没有未被访问过的邻接点,便返回上一个已经访问过的顶点b,访问与其邻接且未被访问的顶点e,置e为已访问。依此类推,直到图中所有顶点都被访问过一次且仅一次,遍历结果为:abdehcfg
DFS的空间复杂度为O(n),采用邻接表时时间复杂度为O(n+e)。
2.5.6 最小支撑树
连通图G的某一无环连通子图T若覆盖G中所有顶点,则称作G的一棵支撑树。若图G为一带权网络,则每一棵支撑树的成本即为其所采用的各边的权重之和,在图G的所有支撑树中,成本最低者称作最小支撑树。
蛮力算法:逐一考察G中所有支撑树并统计其成本,从而选出最低者。
Prime算法:在带权连通图中V是包含所有顶点的集合, U已经在最小生成树中的节点,从图中任意某一顶点v开始,此时集合U={v},重复执行下述操作:在所有u∈U,w∈V-U的边(u,w)∈E中找到一条权值最小的边,将(u,w)这条边加入到已找到边的集合,并且将点w加入到集合U中,当U=V时,就找到了这颗最小生成树。
2.5.7 最短路径Dijkstra算法
从图中某个顶点出发到达另一个顶点所经过的边的权重和最小的一条路径,称为最短路径。
Dijkstra是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。假设G是一个带权图,把图中的顶点集合分为2组:第一组为已求出最短路径的顶点集合,用S表示(初始时S中只有一个源点,以后每求得一条最短路径,就将其加入到结合S中,直到全部顶点都加入到S中,算法结束)。第二组为其余未确定最短路径的顶点集合,用U表示。在加入的过程中,总保持从源点v到S中顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。S中顶点的距离为v到此顶点的最短路径长度,U中顶点的距离为v到此顶点且只包含S中的顶点为中间顶点的当前最短路径。具体过程如下:
① 初始时,S只包含顶点s,U包含除s外的所有顶点,且U中顶点为起点s到该顶点的距离。如U中顶点v的距离为(s,v)的长度,若不相邻,则v的距离为 。
② 从U中选择距离最短的顶点k,并将顶点k加入到S中,从U中移除顶点k。
③ 更新U中各个顶点到s的距离。
④ 重复步骤2和3,直到遍历完所有节点。