[集合DP] UVa10911 最优配对问题 （复杂状态的DP）

题目

思路

本题首先想到用多阶段决策来做，d(i)表示前i个点两两配对的最小距离和，然后考虑第i个点的决策。假设它和点j配对（j < i），那么状态就转移成了前i-1个点除了点j两两配对的最小距离和。显然这个“前i-1个点除了点j”难以用一个简单的d(i)表示，所以在此处引入集合表示。
LRJ：当发现状态无法转移后，常见的方法是增加维度，即增加新的因素，更细致地描绘状态。


此处还有一个困难，就是集合的表达。
此处集合的表达最方便的方法是二进制。

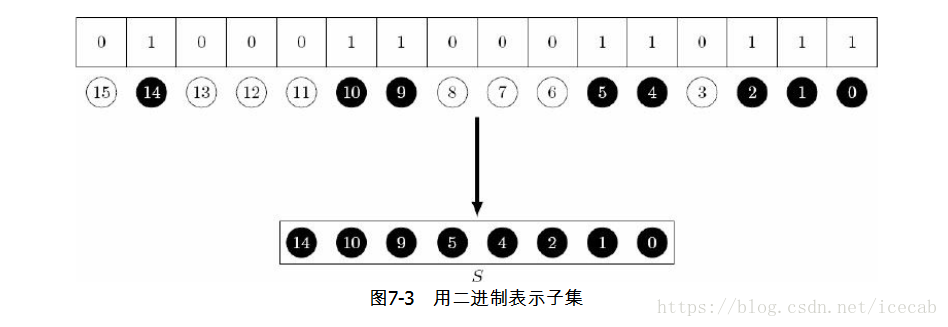
（注意：为了方便，最右边的元素往往是0而不是1）


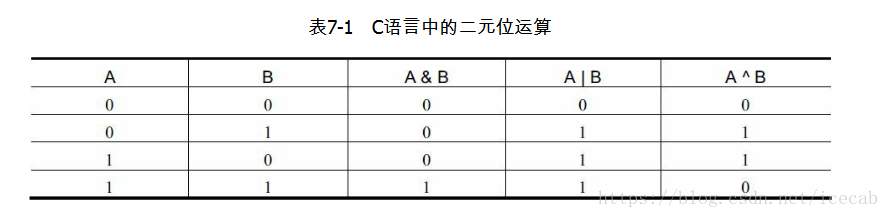
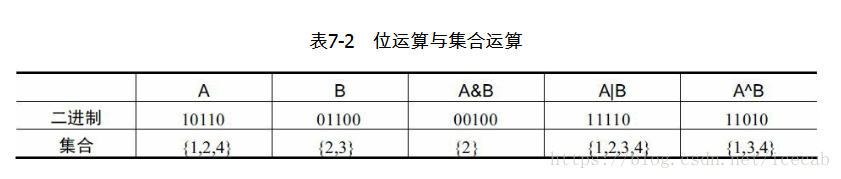
在集合表示法中，1 << i代表单元素集合i，(1 << i)-1表示小于i的所有元素，“S & (1 << j)”不等于0就意味着“S和{j}的交集不为空”，而“S ^ (1 << j)”表示没有j的S集合。


1.状态定义：d(S)，表示子集S里所有点两两配对的最小距离和。
2.边界：d(0) = 0（代码中刻意避开d(0)的枚举）
3.答案：d((1 << n) - 1)
4.状态转移方程：

$$d(S) = min\left\{ |P_iP_j| + d(S-\left\{i\right\}-\left\{j\right\}) | j\in S, i = max\left\{S\right\} \right\}$$
注意此处刻意将i作为S中的最大元素，因为这样枚举i和j只需要 $O(n)$，而 $i \in S, j\in S$需要 $O(n^2)$，不然就会造成下面的转移方程
$$d(S) = min\left\{ |P_iP_j| + d(S-\left\{i\right\}-\left\{j\right\}) | j\in S, i \in S \right\}$$
复杂度变成了 $O(n^22^n)$。
LRJ：即便状态定义相同，过多地考虑不必要的决策仍可能会导致时间复杂度上升，也就是我们需要尽可能地减少决策。
5.复杂度： $O(n 2^n)$
（状态个数为2^n，每个状态的决策需n）


关于本题的递推：
LRJ：如果S`是S的真子集，则一定有S`

代码

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#define _for(i,a,b) for(int i = (a); i<(b); i++)
#define _rep(i,a,b) for(int i = (a); i<=(b); i++)
using namespace std;

const int INF = 1 << 18;
const int maxn = 20 + 2;
const int maxnum = 1 << 20;
int n;
double dist[maxn][maxn], d[maxnum];
struct node {
    int x, y;
}pos[maxn];

int main() {
    freopen("output.txt", "w", stdout);

    int kase = 0;
    while (scanf("%d", &n) == 1 && n) {
        char s[1000];
        n *= 2;
        _for(i, 0, n) scanf("%s%d%d", s, &pos[i].x, &pos[i].y);
        _for(i, 0, n)
            _for(j, 0, n)
                if (i != j) {
                    dist[i][j] = sqrt(pow(pos[i].x - pos[j].x, 2) + pow(pos[i].y - pos[j].y, 2));
                }

        _for(S, 1, 1 << n) {
            int i = 0;
            _for(j, 0, n) {
                if (S & (1 << j)) {
                    i = j;
                }
                if ((1 << j) > S) break;
            }
            d[S] = INF;
            _for(j, 0, i)
                if (S & (1 << j)) {
                    d[S] = min(d[S], dist[i][j] + d[S ^ (1 << i) ^ (1 << j)]);
                }
        }

        printf("Case %d: %.2lf\n",++kase,  d[(1 << n) - 1]);
    }

    return 0;
}