杜教筛学习笔记

QwQ一个不会莫比乌斯反演的蒟蒻来写杜教筛的博客了

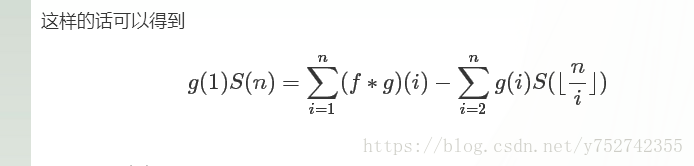
这个是杜教筛的一般形式

中间那个先枚举几倍，实际上相当于把令$i=k*d$ 然后进行k和d枚举

这么空说怎么好理解

我们来引入两道例题吧

$51nod$ 莫比乌斯函数之和

求

$$\sum_{i=1}^{n}\mu(i)$$

一看这个题，貌似没什么头绪呀。

我们可以现推一下

因为$\mu * 1 = e$（或者写成$\sum_{d|n}\mu(d)=[n==1]$

所以

$$\mu(n)=e(n)-\sum_{d|n,d!=n}\mu(d)$$

那么

$$ans=\sum_{i=1}^{n}(e(i)-\sum_{d|i,d!=i}\mu(i))$$

因为$\sum_{i=1}^{n} e(i)=1$

所以

$$ans=1-\sum_{i=1}^{n}\sum_{d|i,d!=i}\mu(i)$$

我们令$i=k*d$，然后分别枚举k和d

$$ans=1-\sum_{k=2}^{n}\sum_{d=1}^{\lfloor \frac{n}{k} \rfloor}\mu(i)$$

这里k从2开始枚举的原因是因为$d!=i$

到这里我们能发现对于$\frac{n}{k}$可以整除分块 且$\sum_{d=1}^{\lfloor \frac{n}{k} \rfloor}\mu(i)$这个式子实际上是一个子问题，可以通过递归求值，只需要记忆化一下，就可以解决了

那么到这里，我们杜教筛的大致思路也就出来了

1.将一些小数的ans值筛出来，然后记忆化
2.对于一个数$x$，我们可以进行分块，然后递归求解

直接上代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#include<unordered_map> 
using namespace std;

inline long long read()
{
  long long x=0,f=1;char ch=getchar();
  while (!isdigit(ch)) {if (ch=='-') f=-1;ch=getchar();}
  while (isdigit(ch)) {x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
  return x*f;
}

const int maxn = 4700000;

int prime[maxn],check[maxn];
int mu[maxn];
int tot;
unordered_map<long long,int> mp;

void init(int n)
{
    mu[1]=1;
    check[1]=1;
    for (int i=2;i<=n;i++)
    {
        if (!check[i])
        {
            prime[++tot]=i;
            mu[i]=-1;
        }
        for (int j=1;j<=tot;j++)
        {
            if (i*prime[j]>n) break;
            check[i*prime[j]]=1;
            if (i%prime[j]==0) break;
            mu[i*prime[j]]=-mu[i];
        }
    }
    for (int i=2;i<=n;i++) mu[i]+=mu[i-1]; 
}

long long l,r;

long long dfs(long long x)
{
    if (x<=maxn) return mu[x];
    if (mp[x]) return mp[x];
    long long ans=1;
    for (long long i=2,j=0;i<=x;i=j+1)
    {
        j=x/(x/i);
        ans=ans-dfs(x/i)*(j-i+1);
    }
    mp[x]=ans;
    return ans;
}

int main()
{
  init(maxn);
  l=read(),r=read();
  cout<<dfs(r)-dfs(l-1); 
  return 0;
}

第二个问题是$51nod$ 欧拉函数之和

其实这两个问题是差不多的

针对这个问题，我们要求的是

$$\sum_{i=1}^{n}\phi(i)$$

还是同样
因为$id=1*\phi$ (或者写成$\sum_{d|n}\phi(d)=n$）

那么

$$\phi(n)=id-\sum_{d|n,d!=n}\phi(d)$$

那我们要求的

$$ans=\sum_{i=1}^{n}(id-\sum_{d|n,d!=n}\phi(d))$$
$$ans=\frac{(n+1)n}{2}-\sum_{i=1}^{n}\sum_{d|i,d!=i}\phi(d)$$
设 $i=k*d$
$$ans=\frac{(n+1)n}{2}-\sum_{k=2}^{n}\sum_{d=1}^{\lfloor \frac{n}{k}\rfloor}\phi(d)$$
$$ans=\frac{(n+1)n}{2}-\sum_{k=2}^{n}ans({\lfloor \frac{n}{k}\rfloor})$$

然后就可以和上一道题一样的思路，直接做就好

上代码（注意取膜的时候的一些注意事项）

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#define ll long long
#include<unordered_map>
using namespace std;

inline ll read()
{
  ll x=0,f=1;char ch=getchar();
  while (!isdigit(ch)) {if (ch=='-') f=-1;ch=getchar();}
  while (isdigit(ch)) {x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
  return x*f;
}

const int maxn = 6e6+1e2;
const ll mod = 1e9+7;

ll phi[maxn];
ll prime[maxn];
int check[maxn];
ll l,r;
int tot;

ll qsm(ll i,ll j)
{
    ll ans=1;
    while (j)
    {
        if (j&1) ans=ans*i%mod;
        i=i*i%mod;
        j>>=1;
    }
    return ans;
}

ll inv = qsm(2,mod-2);

unordered_map<long long,long long> mp,mp1;

void init(ll n)
{
    phi[1]=1;
    check[1]=1;
    for (int i=2;i<=n;i++)
    {
        if (!check[i])
        {
            prime[++tot]=i;
            phi[i]=i-1;
        }
        for (int j=1;j<=tot;j++)
        {
            if (i*prime[j]>n) break;
            check[i*prime[j]]=1;
            if (i%prime[j]==0)
            {
                phi[i*prime[j]]=phi[i]*prime[j]%mod;
                break;
            }
            else
            {
                phi[i*prime[j]]=phi[i]*(prime[j]-1)%mod;
            }
        }
    }
    for (int i=2;i<=n;i++) phi[i]=(phi[i]+phi[i-1])%mod;
}

ll dfs(ll x)
{
    if (x<=maxn) return phi[x]%mod;
    if (mp1[x]) return mp[x]%mod;
    long long ans=x%mod*(x%mod+1)%mod*inv%mod;
    for (ll i=2,j=0;i<=x;i=j+1)
    {
        j=x/(x/i);
        ans=(ans-(j-i+1)%mod*dfs(x/i)%mod+mod)%mod;
    }
    ans=(ans%mod+mod)%mod;
    mp[x]=ans;
    mp1[x]=1;
    return ans;
}

int main()
{
  init(maxn-10);
  l=read();
  cout<<dfs(l)%mod;
  return 0;
}