马尔科夫随机场之图像分割【二】

参考：http://blog.csdn.net/on2way/article/details/47307927从贝叶斯理论到图像马尔科夫随机场

刘伟强等；基于马尔科夫随机场的遥感图像分割和描述；东南大学学报；（29）：11-15，1999

version:2017.1.20 基本理解框架

Markov Random Filed

一、理论基础

马尔科夫随机场是一种基于统计的图像分割算法。它的特点主要为模型参数少、空间约束性强

马尔科夫模型是一组事件的集合。在这个集合中，事件是逐个发生，并且下一刻事件的发生只由当前发生的事件决定，而与再之前的状态没有关系。拿博主【我爱i智能】之天气的例子说明为，【今天天气好坏只与昨天天气有关，而与前天乃至大前天都没有关系】，引申到图像领域为：图像中某一点特征（一般指灰度值、RGB值等）只与其附近的一小块邻域有关，而与其他的邻域无关。

二、基于图像分割应用

关于图像分割问题，从聚类角度讲，就是一个图像聚类问题，把具有相同性质的像素点设置为一类。也就是一个标签分类问题，比如把一副图像分割成4类，那么每一个像素点必定属于这四类中的某一类，假设四类为1，2，3，4类，那么分割就是给每个像素点找一个标签类。好了，假设我们的待分割图像是S，大小m*n，那么把每个像素点放到集合S中，图像就是：，把待分割的图像称为观测到的图像。现在假设分割好了，每个像素点都分了类，那么把最终的分割结果称为W，那么显然w大小与S一样大，,其中所有的w取值都在1-L之间，L是最大的分类数，比如上面L=4，那么每个w都是在1-4之间取值的。这是我们假设知道了最终分割结果W，但是W在开始是不知道的。现在的问题就是如何求W，我们所知道的不过是观测到的图像S，也就是说在知道S情况下求W，转化为概率就是求取P(W|S),问题就变成求取这个概率的最大值，也就是说根据S算出这个图像的最有可能的分割标签是什么。

基于此，问题才刚刚开始。我们由贝叶斯理论知道

上式先不看是否能求，先给一些定义。

W就是要求的分类标签，称P(W)为标记场w的先验概率（要求它，事先又不知道，那就叫先验概率吧，不知道是不是这样来的）。
P(S|W)是观察值S的条件概率分布（也称似然函数），看结构为在已知像素点标记w情况下，它是真实的像素点s概率，所以是一个似然函数，表示我的观察像素点和真实的分类情况w像不像的一种程度。
P(S)是什么？S是观察到的图像，在分割前它就已经定了，我就要分割这幅图像，那它还有概率吗？没有吧，所以P(S)认为是个定值。

那么现在要求P(W|S)的最大值，也就是要求P(S|W)P(W)的最大值。

先来说说P(W)这个标记场w的先验概率。落实到图像每一个像素点上，即为该像素点是标签L的概率是多少。有人可能会说，分割之前图像的分类标签都不知道，还怎么算是某一类标签L的概率？

这个问题是有点较劲不好理解。我觉得，这就是一个鸡蛋问题，是先有鸡还是先有蛋的问题，我们要求这只鸡，但是又没有蛋怎么办？一个简单的办法是我随便弄一个蛋来，管他是鸡蛋鸭蛋，有了蛋，鸡（或者鸭）就可以有了，虽然这个鸡不太像鸡，比如说是只野鸡，那么有了野鸡，野鸡再稍微进化一下，然后再下个蛋，蛋又长出野鸡1号，野鸡1号再稍微进化一下，然后再下个蛋，变成野鸡2号，如此反复反复，知道野鸡n号，然后蓦然回首发现，野鸡n号和我们所要的鸡竟是那么的相似，那么把它就认为是我们要的鸡了。有没有糊涂？其实优化聚类里面很多问题都是鸡蛋问题，比如曾经介绍的FCM算法，有个先给u还是先给c的鸡蛋问题，u的计算需要c，c的计算有需要u，那怎么办，先假设一个吧。再比如EM算法的迭代过程也可以看成鸡蛋问题，有了E步算M步，在回来算E步，在M步。。。。最终得到最优解。

好，回到我们的问题，求一个像素点是标签L的概率，开始标签没有，ok假设一个吧，一个不行，那么在开始我们把整幅图像初始化一个分割标签，尽管这个标签不对（野鸡），也可以假设一个稍微对一点的标签（比如用其他分类算法（kmeans）得到一个预分割标签）（这个时候认为是野鸡100号）（好处在于这个时候算法不用迭代那么多次就可以停止了）。好了有了初始的标签，那么再来求一个像素点是标签L的概率。从这个时候就需要马尔科夫协助了。我们想，要求一个像素点是标签L的概率，此时这个像素点附近的邻域都已经划分标签了，虽然这个像素点也有一个标签，但是这个标签是上一代的标签，那么它到下一代是需要进化的，马尔科夫性质告诉我们这个像素点的分类情况只与附近一些邻域分类情况有关，而与另一些邻域没有关系，也就是说我们可以根据这个像素点附近邻域的分类情况决定这个像素点在下一代是属于哪一类的。

补充：马尔科夫随机场是以其局部特性（马尔科夫性）为特征的，吉布斯随机场是以其全局特性（吉布斯分布）为特征的。Hammersley-Clifford定理则建立了这两者之间的一致关系。

Hammersley-Clifford定理可知，要定义一个马尔科夫随机场，由于它与一个吉布斯随机场相对应，如果定义了该吉布斯随机场的能量函数，那么这个马尔科夫随机场也就确定了

MAP：Maximum A Posterior，最大后验概率估计

势团势能：（待补充）

Ok，既然我们认为每个像素点的分类符合马尔科夫随机模型，而另一些学者证明了这种马尔科夫随机场可以与一个Gibbs随机场等价（这就是Clifford-Hammersley定理，人家证明的，那就这样叫吧）。而Gibbs随机场也有一个概率密度函数，这样我们就用求图像的Gibbs随机场的概率P代替了P(W)。那么Gibbs随机场的概率P怎么表示呢？如下：

其中，是归一化常数，参数T可控制P（w）的形状，T越大越平坦。而，C为所有势团集合，为势团势能。对的定义如下：

为耦合系数，通常0.5-1。
糊不糊涂，不糊涂才怪，这么多关系，Gibbs也不容易，还没完，那么什么是势团，说白了就是和这个像素点构成一个小的【检测这个点连通性能】的区域，一个图如下：

总算完了，乍一看真是复杂，不知所云，其实细看还是可以理解的。说白了就是检测一下这个点和周围邻域的相似程度。那些势团就是要比较的对象。举个例子，以一阶势团为例，假设某个点及其附近的8领域在某次迭代后的分类标签是这样的（假设分四类的情况）：

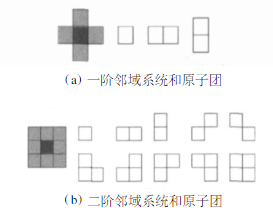
现在要计算中心的像素点在下一次迭代中是属于第几类（这一代是第3类），ok采用一阶势能，这里需要说明一点，这个像素点无非是1-4之间的一类，那么我们需要分别计算下一代它是第1,2,3,4类时的势团。先假设这个点是第1类，先比较左右，发现都是1-1一样，ok记一下,在与上，与下，不一样，那么记一下，如果再来势团的话，斜上方，1-2，不一样，斜下方，1-1一样，，一次类推，就可以将中心点如果是第1类的势团计算出来。那么在计算中心点如果是第2类，发现这个时候除了3个斜着的方向是一样的外，其他的都不一样。在计算假设是第三类，第四类。这样有了每类下的势团，就可以计算概率了，根据公式往回带呀带，最终得到这个点如果属于第一类的概率，第二类的概率，第三类的概率，第四类的概率，这四个值在后面会一起用到来决定这个点到底属于哪一类。你可能会说，知道了这四个概率，看哪个最大不就出来了吗？注意这还只是第一项的先验概率，后面还有个似然函数的概率没有计算呢，后面你会看到这个似然函数的概率对于每个像素点也有四个概率，在这四个概率都计算出来之后，那么这个点属于第一类的概率用着两个都属于第一类的概率相乘，第二类也是如此，最后再比较这四个概率的最大值作为要标记的标签。

通观Gibbs，其实就是一个求像素点与周围像素点的不一致程度，或者说这个像素点的周围像素点中，看看各个标签出现的概率多大，就是这个点属于对应标签的概率。所以在实际编程上，也没看到几个人实实在在的用它的原版公式编程，反而简化的计算，看看各个标签出现的次数等等方式来计算的。

关于P(W)就说这么多，下面说说P(S|W)。P(S|W)，已知分类标签那么它的像素值（灰度）是s的概率。现在就假设w=1，某个像素点灰度为s，那么表示的意思就是在第一类里面像素灰度为s的概率。因为分类标签在前面说到，每次迭代的时候是有一个分类标签的（尽管不是最后的标签），那么我们可以把属于第一类的所有点都挑出来，考虑每个点都是独立的，并且认为每一类里面的所有点服从高斯分布（正态分布），那么在每一类里面我们是不是可以根据这一类里面的这些点建立一个属于这一类的高斯密度函数了，那么再来一个像素点值，把它带到这类里面密度函数中去就可以得到这个概率了吧。同理对于2,3,4类，每一类都可以建立一个高斯密度函数，这样就有四个高斯密度函数了，那么每一个点属于这四类的概率就可以分别带到这四个高斯密度函数中计算了。高斯密度函数一般形式为：

举个例子假设现在我们求得的四类高斯函数，其图像如下所示：
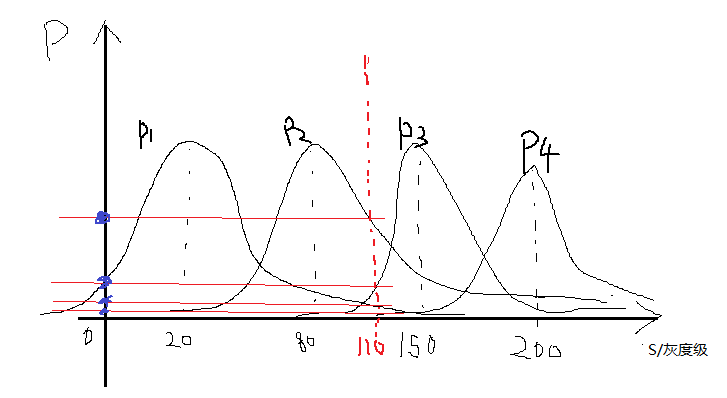
这里写图片描述

某一点的灰度为s=110，那么它对应的分别P(s|W1)、P(s|W2)、P(s|W3)、P(s|W3)，就分别如上图所示呢，很显然的可以看到110在第三类下的概率最大，其他的几个概率也可以出来的。

现在这一部分对于每个点也有了四个概率，结合上面每个点的四个概率，那么对每个点，属于每一类的概率对应相乘，得到最终每个点属于四个类的概率。这个时候就可以挑其中最大的那么就是该点所属于的类了。这样一次迭代，所有的点所属于的类更新一遍，那这个新的类标签作为下一次迭代的类标签，反复下去，程序结束的条件可以是设置迭代次数，也可以是观察类中心不在变化为止。
好了，上述的概率相乘取最大是原始一点的算法。其实可以看到，这个计算包括两个部分，一般的讲法，认为这两部分每一部分都组成一个能量，换个说法就是最优化能量函数了，可以表示为如下：

像上述的概率相乘在实际中取一下对数就变成相加了。更深层次的马尔科夫随机场可以去看看相关论文，虽然方法可能不太一样，但是原理上是一样的。

下面以条件迭代算法（ICM）来实例阐述MRF在图像分割上的应用，编程平台为matlab，相关代码如下：

clc
clear
close all
img = double(imread( 'lena.jpg'));%more quickly
cluster_num = 4;%设置分类数
maxiter = 60;%最大迭代次数
%-------------随机初始化标签----------------
label = randi([ 1,cluster_num],size(img));
%-----------kmeans最为初始化预分割----------
% label = kmeans(img( :),cluster_num);
% label = reshape( label,size(img));
iter = 0;
while iter < maxiter
%-------计算先验概率---------------
%这里我采用的是像素点和 3* 3领域的标签相同
%与否来作为计算概率
%------收集上下左右斜等八个方向的标签--------
label_u = imfilter( label,[ 0, 1, 0; 0, 0, 0; 0, 0, 0], 'replicate');
label_d = imfilter( label,[ 0, 0, 0; 0, 0, 0; 0, 1, 0], 'replicate');
label_l = imfilter( label,[ 0, 0, 0; 1, 0, 0; 0, 0, 0], 'replicate');
label_r = imfilter( label,[ 0, 0, 0; 0, 0, 1; 0, 0, 0], 'replicate');
label_ul = imfilter( label,[ 1, 0, 0; 0, 0, 0; 0, 0, 0], 'replicate');
label_ur = imfilter( label,[ 0, 0, 1; 0, 0, 0; 0, 0, 0], 'replicate');
label_dl = imfilter( label,[ 0, 0, 0; 0, 0, 0; 1, 0, 0], 'replicate');
label_dr = imfilter( label,[ 0, 0, 0; 0, 0, 0; 0, 0, 1], 'replicate');
p_c = zeros( 4,size( label, 1)*size( label, 2));
%计算像素点 8领域标签相对于每一类的相同个数
for i = 1 :cluster_num
label_i = i * ones(size( label));
temp = ~(label_i - label_u) + ~(label_i - label_d) + ...
~(label_i - label_l) + ~(label_i - label_r) + ...
~(label_i - label_ul) + ~(label_i - label_ur) + ...
~(label_i - label_dl) +~(label_i - label_dr);
p_c(i, :) = temp( :)/ 8;%计算概率
end
p_c(find(p_c == 0)) = 0 . 001;%防止出现 0
%---------------计算似然函数----------------
mu = zeros( 1, 4);
sigma = zeros( 1, 4);
%求出每一类的的高斯参数--均值方差
for i = 1 :cluster_num
index = find( label == i);%找到每一类的点
data_c = img( index);
mu(i) = mean(data_c);%均值
sigma(i) = var(data_c);%方差
end
p_sc = zeros( 4,size( label, 1)*size( label, 2));
% for i = 1 :size(img, 1)*size(img, 2)
% for j = 1 :cluster_num
% p_sc(j,i) = 1/sqrt( 2*pi*sigma(j))*...
% exp(-(img(i)-mu(j))^ 2/ 2/sigma(j));
% end
% end
%------计算每个像素点属于每一类的似然概率--------
%------为了加速运算，将循环改为矩阵一起操作--------
for j = 1 :cluster_num
MU = repmat(mu(j),size(img, 1)*size(img, 2), 1);
p_sc(j, :) = 1/sqrt( 2*pi*sigma(j))*...
exp(-(img( :)- MU).^ 2/ 2/sigma(j));
end
%找到联合一起的最大概率最为标签，取对数防止值太小
[~, label] = max(log(p_c) + log(p_sc));
%改大小便于显示
label = reshape( label,size(img));
%---------显示----------------
if ~ mod(iter, 6)
figure;
n= 1;
end
subplot( 2, 3,n);
imshow( label,[])
title([ 'iter = ',num2str(iter)]);
pause( 0 . 1);
n = n+ 1;
iter = iter + 1;
end

现在假设把图像分两类cluster_num=2，采用随机初始化分类，贴几个之间结果：
这里写图片描述

将分类数设置为cluster_num=4，贴几个中间结果：

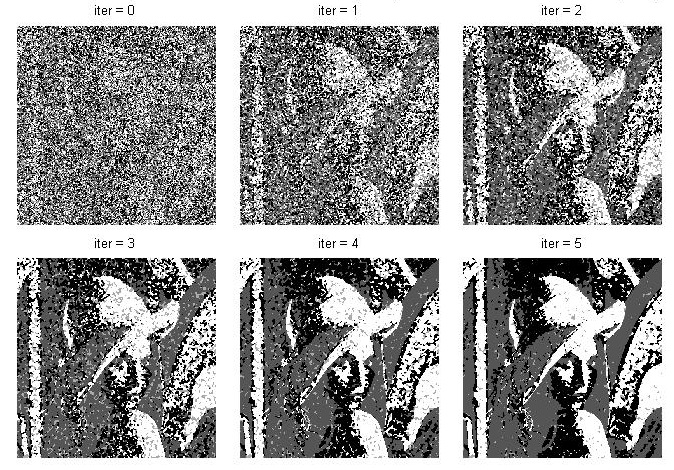
这里写图片描述

上述程序除了注释外再说一点，那就是对于是否需要预分类，程序里面写了随机分类和kmeans预分类两者，贴的结果都是在随机初始化的分类。当分别去实验可以发现，如果采用kmeans预分类后，迭代开始分割的结果就很好，程序会在这个基础上再变化一点，采用kmeans预分类的好处在于，分割的结果会更快达到稳定，且更准确。而采用随机的预分类，分割的结果也算可以，这种方法得到的是一个局部最优解，当然kmeans得到的也是个局部最优解（不敢说最优解），但是前面的局部最优解比kmeans后的局部最优解又会差一点，尤其是在分割类别数大一点的时候，有kmeans预分类的效果会明显好于随机预分类。因为类别数越是大，相当于维度就越是大，那么它存在的局部最优解就越是多，那么从随机的预分类（最差的情况）往最优解方向走时，中途可能随便碰到一个局部最优解就走不动了。从某种意义上讲，这个分割是一个np难问题，很难找到分割的最优解。

马尔科夫随机场之图像分割【二】

猜你喜欢